| [65] Kristóf Miklós 3 | 2014-02-05 19:47:35 |
 Kedves Mindenki, jó 3 és fél év telt el mióta utoljára írtam a Kömal Fórumba. Most sokkal érettebb vagyok, és sokkal többet tudok. 2011 szeptember 21-én megvilágosodtam, és rájöttem hogy 30 évig rossz adatokkal számoltam, ezért nem is volt érdemi eredményem. Amikor rájöttem a helyes éter (TIP) állandókra, minden a helyére került. Ezekről olvashattok a www.kvadromatika.fw.hu weboldalamon, éterelmélet alcím, azon belül az Új TIP Kozmológia és a TIP Adatbázis cikkekben. A többi is érdekes (elektrogravitáció kísérleti igazolása) Úgyhogy szeretettel invitállak titeket erre a topikra!
|
|
| [64] Kristóf Miklós 2 | 2010-10-11 14:17:37 |
 Kedves Mindenki, kétféle hang van: az ismert longitudinális hang, ami a nyomás hullámszerű terjedése, és van az áramláshullám, ami transzverzális, azaz a gyorsulás, a sebesség rotációja és a hullám terjedési iránya egymásra merőleges. Lehetséges hogy ezt a hangot még nem fedezték fel? De lehet hogy felfedezték, csak nem közismert. Lehet hogy a rezgésszáma nagyon magas, vagy nagyon alacsony. Ultrahang vagy infrahang. Ultrahang mikroszkópot se csináltak még, pedig milyen jó lenne, bele lehet látni vele az anyag belsejébe. A nanotechnológia is hasznát venné.
|
|
|
| [62] Kristóf Miklós 2 | 2010-10-05 18:30:04 |
 A transzverzális elektromágneses hullám
 = az áramló éter sebessége. = az áramló éter sebessége.
S=sin(k.x- .t) .t)
C=cos(k.x- .t) .t)
vx,vy,vz,k, tetszőleges állandók, c = fénysebesség. tetszőleges állandók, c = fénysebesség.
 a hullámszámvektor, x irányban terjed. a hullámszámvektor, x irányban terjed.


v2=(vx2+vy2+vz2).S2




Az újmaxwell egyenlet szerint  , mert üres vákuumban nincs töltés. , mert üres vákuumban nincs töltés.
Mivel sem  , sem k, S, sem C nem nulla, marad az, hogy vx=0 . , sem k, S, sem C nem nulla, marad az, hogy vx=0 .
Tehát  , ,
 , ,


Jól látható, hogy  , ,  és és  egymásra merőlegesek. egymásra merőlegesek.
Íme, tehát megkaptuk a transzverzális elektromágneses hullámot!
Gyerekek, semmit ne higgyetek el nekem, számoljatok utána!
A másik újmaxwell egyenlet szerint  kell legyen. kell legyen.





Tehát a hullám fénysebességgel terjed.
Mindenben a tapasztalattal egyező eredményt kaptunk.
Tehát az újmaxwell egyenletek nem vezetnek ellentmondásra.
|
|
| [61] Kristóf Miklós 2 | 2010-10-05 17:05:37 |
 Kedves bily71, nem baj ha nem vagy beavatott, majd én beavatlak, persze csak ha akarod. Viszont az nem megy hogy csak a végeredményre vagy kíváncsi. Itt sincs királyi út, végig kell menned a szükséges lépcsőfokokon. Enélkül nem érted a végeredményt. Mivel fizikus voltam, tudok ilyen elemi dolgokról hogy kísérletileg is igazolni kell. De nem azonnal. Einstein relativitáselméleét is csak 1918-ban igazolták csillagászati megfigyeléssel, addig az csak hipotézis volt. Olyan Univerzum, aminek nincs kapcsolata a miénkkel, nem létezik. Így vizsgálata valóban fölösleges. Ami az elnevezést illeti: a "világ" szó a Földet jelenti, sokáig ez volt "a minden". Utána az Univerzum azt a világbuborékot jelentette amely 13.7 milliárd évvel ezelőtt keletkezett (már ha elfogadjuk a Big Benget) Nos, ez sem " a minden". Ezért találták ki a Multiverzum szót, ezt se az ujjamból szoptam. Ezen már rajtaragad ez a név, el kell fogadnod.
|
| Előzmény: [60] bily71, 2010-09-29 12:43:42 |
|
| [60] bily71 | 2010-09-29 12:43:42 |
 Igen, én nem vagyok beavatott, szerintem nem is leszek, pusztán csak mint "mükedvelőt" érdekel ez a téma, inkább filozófiai szemszögből vizsgálom, ezért én csak a végkövetkeztetésre vagyok kiváncsi,
Egyébként azt tudtad, hogy a fizikában az elméletet muszály igazolni kisérletekkel, addig az csak feltételezés, nem pedig törvény?
A másik, szerintem olyan univerzumokat vizsgálni, melyeknek nincs kapcsolata a mi Univerzumunkkal teljesen felesleges, csak fantáziálgatás, spekuláció, hiszen belőlük semmi információ nem jön át, és nem is mehet át.
Ha pedig van Multiverzum, és ahogy irod: "Tehát nagyon sok Univerzum van, melyek képesek egymásba átmenni. Vannak átjárók köztük.", vagyis van információnk róluk, van valamilyen kölcsönhatás közöttük (energia-,anyagáramlás, mezők kölcsönhatása, stb.), akkor Multiverzum=Univerzum, ugyanis a Világmindenség, ami a neve szerint magábafoglal MINDENT, minden információt (tehát a Multiverzumok tartalmát is), csak egy lehet, mint ahogy Semmi is csak egy lehet. Ilyen értelemben szerintem nem létezhet Multiverzum.
|
| Előzmény: [59] Kristóf Miklós 2, 2010-09-29 11:37:39 |
|
| [59] Kristóf Miklós 2 | 2010-09-29 11:37:39 |
 Kedves bily71, amit írsz az a kisérleti fizikusokra igaz. Az elméletiek már képletekben gondolkodnak. Persze a fene tudja. Nálam a képlet csak a végeredmény. A többiek sem kötözködnek, csak kíváncsiak, és precizitást várnak. A beavatottak félszóból értenek. Írt nekem egy fizikus hallgató srác, el van bűvölve, milyen jól levezettem az étert, milyen szemléletes. A vak Lajos bácsinak a vécére kimenni is nehéz, nekem meg Párizs sincs túl messze. Így megy ez.
Az éter összehúzódik, kis buborékokba tömörül, melyek mérete 10-35 méter. Az éter a buborékokon kívül is van, áramlik a buborékok felé. Az Univerzum is egy buborék, és az éter rajta kívül is van, áramlik a buborék felé. Nagyon sok buborék van egymás mellett, és ezek kristályrács-szerűséget alkotnak. Ez a Multiverzum. Tehát nagyon sok Univerzum van, melyek képesek egymásba átmenni. Vannak átjárók köztük. Az éter tehát az egész Mindenséget betölti. A Mindenség kis buborékokba cseppesedik. Ahogy a buborékok a szappanhabban. Vagy az atomok a kristályrácsban.
|
| Előzmény: [58] bily71, 2010-09-27 14:21:09 |
|
| [58] bily71 | 2010-09-27 14:21:09 |
 Na de, ha létezik az éter, akkor az egész Univerzum úszik az éteren át, tehát az éter azon kivül is létezik, nem?
Én a többiekkel ellentétben nem kötözködöm, csak kiváncsi vagyok a világ-modelledre, mert a képletekből az nem "látszik ki". Pár mondattal ird le, de képlet nélkül.
A gimiben a fizika órákból egyvalami nagyon megmaradt bennem, a tábla fölé ez volt irva nagybetükkel: "Egy fizikus sem gondolkodik képletekben." , nem tudom kitől származik, de találó.
|
| Előzmény: [53] Kristóf Miklós 2, 2010-09-27 10:25:52 |
|
| [57] Kristóf Miklós 2 | 2010-09-27 10:49:17 |
 Kedves Fernando, kérdezz konkrétan, és akkor konkrét választ kapsz.
Egyszerűbb fizika? Nos, vesd össze az enyémet a húrelmélettel meg a tenzoranalízisre épülő einsteini elmélettel! Próbálj meg azokba belekötni!
|
| Előzmény: [50] Fernando, 2010-09-25 07:33:11 |
|
| [56] Kristóf Miklós 2 | 2010-09-27 10:47:06 |
 Kedves Fernando, ha a RUT modellt úgy képzelem hogy a rugók merev rudakként kötik össze az atomokat, akkor valóban merev testet kapok. Ám a RUT modell fejlettebb változatánál az éteratomok közt az ismert newtoni  erő hat. Az erőket minden atomra összegzem. Ennek eredménye az, hogy az egész atomrács egy kritikus méretre összehúzódik, ott stabil marad, és ha kimozdítok egy atomot, arra F=-k.x erő hat, ahol k a rugóállandó, számolható. Ezt úgy hívom hogy Shira-felösszegzés. erő hat. Az erőket minden atomra összegzem. Ennek eredménye az, hogy az egész atomrács egy kritikus méretre összehúzódik, ott stabil marad, és ha kimozdítok egy atomot, arra F=-k.x erő hat, ahol k a rugóállandó, számolható. Ezt úgy hívom hogy Shira-felösszegzés.
Fejlettebb változatánál az  erőt használom. Ja, m1=m2=m0 veendő. erőt használom. Ja, m1=m2=m0 veendő. 
"A fizika nem úgy működik, hogy fogok és szépen kiszámolok mindent! Nem, az elméleti fizika sem.. :) "
Tényleg? Hát én ennek a szöges ellentétét tapasztaltam!
|
| Előzmény: [49] Fernando, 2010-09-25 07:26:22 |
|
| [55] Kristóf Miklós 2 | 2010-09-27 10:35:02 |
 Kedves Fernando, persze igazad van, de az éter atomjai 10-35 méter nagyok, ilyen méretekben nyugodtan használhatunk folytonos határátmenetet, és a Van der Waals féle elfajulással se kell számolni, amellett az éter ideális gáznak tekinthető. Mi erre a bizonyíték? A tapasztalat. A bolygók évmilliárdok alatt sem fékeződnek.
A RUT modell elsősorban kristályokra lett kidolgozva, de bizonyos feltételek mellett gázokra is jó. ( kis amplitudójú kitérések a rezgéseknél)
Az éter hőmérséklete érdekes téma, lehet diszkutálni.
|
| Előzmény: [48] Fernando, 2010-09-25 01:47:04 |
|
| [54] Kristóf Miklós 2 | 2010-09-27 10:29:44 |
 Kedves Fernando, egy hangszóróból kiszedett mágnest használtam. Egy neodímium mágnes jobb. Mérni meg két kvarcórával kell, először mágnes nélkül, utána mágnessel, és összehasonlítani. Valóban több mérés kell, és statisztikát képezni. A rádió által bemondott pontosidő jobb módszer. Hallottál a Philadelphia kísérletről? A "nagyok" már tengeralattjárókat tudnak eltüntetni és teleportálni erős mágneses terekkel!
|
| Előzmény: [47] Fernando, 2010-09-25 01:33:10 |
|
| [53] Kristóf Miklós 2 | 2010-09-27 10:25:52 |
 Kedves bily71, asszem tudom mire vonatkozik a kérdésed. Az Univerzum sugara nagy, de véges. Egy véges de határtalan háromdimenziós gömb, azaz egy háromdimenziós felületű négydimenziós buborék. Nincs fala, mégis véges. Véges a háromdimenziós térfogata is.
|
| Előzmény: [46] bily71, 2010-09-24 14:53:40 |
|
| [52] Fernando | 2010-09-25 19:45:56 |
 Ez jó ötlet! Mégis szükség lenne az óra mágneses tér nélküli hibáinak megállapítására, tehát komoly méréssorozatra mágneses tér nélkül és egy méréssorozatra mágneses térrel. A kettő adatsort statisztikai eszközökkel összehasonlítani. Ezután meg kell vizsgálni, hogy mi okozza különbséget, --sok technikai oka is lehet-- ha az szignifikáns.
|
| Előzmény: [51] jonas, 2010-09-25 15:28:06 |
|
| [51] jonas | 2010-09-25 15:28:06 |
 Szerintem konyhai eszközökkel is könnyű mérni, hogy a kvarcóra mennyit siet: a konyhai rádión minden délben meghallgatod a pontos idő jelzést, miközben nézed, mennyit mutat az óra. Ezt tapasztalatból tudom, régen még nem az internetről állítottam be az órákat.
|
| Előzmény: [47] Fernando, 2010-09-25 01:33:10 |
|
| [50] Fernando | 2010-09-25 07:33:11 |
 Kedves Miklós!
"A régi fizikától egy új, jobb és egyszerűbb fizika felé!" Ezt a célkitűzést magamtól is gondoltam. Nem erre vonatkozott a kérdés, hanem sokkal konkrétabb dolgokra!
Az "egyszerűbb fizikát" nagyon vitatnám...
|
| Előzmény: [25] Kristóf Miklós 2, 2010-09-15 17:12:14 |
|
| [49] Fernando | 2010-09-25 07:26:22 |
 A rugó-tömeg modell a gáztulajdonságok többségének homlokegyenest ellentmond. (pl. a gáznak nincs önálló alakja, kitölti a rendelkezésre álló teret stb...) A rugó-tömeg modellből nem kunszt kihozni, hogy az transzverzális hullámot is tud közvetíteni. Azt nem tudom, hogy a "rugalmas hullám" mit takar.
A fizika nem úgy működik, hogy fogok és szépen kiszámolok mindent! Nem, az elméleti fizika sem.. :)
Kell egy modell, kellenek feltételezések, amikből kiindulunk, természetesen az eredmény ezektől függ.
|
| Előzmény: [40] Kristóf Miklós 2, 2010-09-24 11:04:12 |
|
| [48] Fernando | 2010-09-25 01:47:04 |
 "A kinetikus gázelmélet kimutatja, hogy a gázban a p.V=N.k.T összefüggés érvényes." -Ez az összefüggés csak erősen korlátozott körülmények között érvényes.
"A gáz ezért modellezhető a Rugó-Tömeg modellel (RUT) ahol az atomokat kis m0 tömegű golyók jelképezik, melyeket k0 rugóállandójú rugók kötnek össze." - Semmi összefüggést nem látok a feljebbi állításoddal, tehát az "ezért"-et vitatom. (anélkül mindjárt más a mondat) - Ezt a modellt nem gázokra alkalmazzuk, hanem pl ionrácsokra, kristályokra, bizonyos hőmérsékleti tartományokban. Egyáltalán nem alkalmas gázok leírására.
|
| Előzmény: [40] Kristóf Miklós 2, 2010-09-24 11:04:12 |
|
| [47] Fernando | 2010-09-25 01:33:10 |
 Kedves Miklós!
Ismét hiányolom a konkrétumokat. "Egy erős mágneses térbe tett jó kvarcóra sietni fog, mondjuk 2 nap alatt egy másodpercet." Mi az erős mágneses tér? 1 T? 10 T? 0,1 T?
Két nap alatt egy másodpercet a jó kvarcóra külső mágneses tér nélkül is késik. Ezt otthon, konyhai eszközökkel nehéz mérni, ugyanakkor kizártnak tartom, hogy az alapkutatásban a mágneses tér kapcsán ilyen alapvető (és laboratóriumi eszközökkel aránylag könnyen elvégezhető) kísérletet ne végeztek volna el, és főleg ne publikáltak volna (profi eszközökkel aránylag könnyen mérhető és nagy szenzáció lett volna az eredmény...) ilyen nyilvánvaló összefüggést...
|
| Előzmény: [45] Kristóf Miklós 2, 2010-09-24 12:07:38 |
|
|
| [45] Kristóf Miklós 2 | 2010-09-24 12:07:38 |
 A vektorpotenciálnak van még egy mérhető hatása:
gyorsítja az időt.
Egy erős mágneses térbe tett jó kvarcóra sietni fog, mondjuk 2 nap alatt egy másodpercet.
Azért siet és nem késik, mert az elektromágneses térnél a Lorentz faktor  jellegű. jellegű.
Ennek bizonyítéka a relativisztikus Dirac egyenlet energiaspektruma a
hidrogénatom esetén, ami  jellegű. jellegű.
Ennek sorfejtése adja a Balmer-szinteket.
v itt az elektron sebessége a mag körül.
Alapállapotban v= .c, ahol .c, ahol  . .
h = planck-állandó = 1.054 E -34 Js
e = 1.5189183 E -14  = 1.602 E -19 Cb = 1.602 E -19 Cb
|
| Előzmény: [44] Kristóf Miklós 2, 2010-09-24 11:56:00 |
|
| [44] Kristóf Miklós 2 | 2010-09-24 11:56:00 |
 Még valami:
A vektorpotenciál mérhető, pl. a Josephson effektussal, ahogy a feszültség is mérhető pl. voltmérővel.
A vektorpotenciál nem abszolút, ahogy a feszültség se az, valami nullponthoz kell viszonyítani.
Nálunk a viszonyítási pont a végtelenben van, ott az  -nak el kell tűnnie. -nak el kell tűnnie.
|
| Előzmény: [43] Kristóf Miklós 2, 2010-09-24 11:52:54 |
|
|
|
| [41] Kristóf Miklós 2 | 2010-09-24 11:11:04 |
 Kedves Alma, természetesen igazad van, ha a térben töltéseloszlás van jelen.
Ekkor  az egyenlet. az egyenlet.
 . .
Ennek megvan a gravitációs megfelelője is:

Amikor az üres vákuumot nézzük, akkor 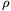 =0, és így =0, és így
a  egyenlet az érvényes. egyenlet az érvényes.
|
| Előzmény: [37] Alma, 2010-09-22 16:03:47 |
|
