Fórum: Prímtulajdonság

Szeretnél hozzászólni? Jelentkezz be.

[8] Károly

2006-08-14 15:23:21

Válasz a [6]-os hozzászólásban feltett kérdésre:

Ha p $\in$ M\K és h(p)=p, akkor p prím.

Biz.: p $\angle$ ab azt jelenti, hogy valamilyen x-szel px=ab. Ekkor

p = h(p) = h(px) = h(ab) = vagy h(a) vagy h(b)

Ha p = h(a) áll fenn, akkor a = h(a)t(a) = pt(a) miatt p $\angle$ a. Ha p = h(b), akkor ugyanígy p $\angle$ b.

És, hogy ne csak én izmozzak itt egyedül, a [7]-beli feladat még érvényes:-))

Üdv

Károly

Előzmény: [6] Károly, 2006-08-10 16:15:52

[7] Károly	2006-08-13 11:17:15
Feladat: Mutassuk meg, hogy ha a monoid csoport, akkor K vagy {e} vagy Ø, és h konstans!

[6] Károly

2006-08-10 16:15:52

Más megközelítésben: Legyen (M,) egy monoid (az egymásmelléírással jelölt M×M $\mapsto$ M szorzással, és legyen h és t két M $\mapsto$ M függvény; továbbá legyen K egy részhalmaz M-ben (ők a "különleges" elemek). Ekkor HT-rendszernek nevezem azt az (M,,h,t,K) struktúrát, amelyre az alábbi axiómák teljesülnek:

1. x=h(x)t(x) $\forall$ x $\in$ M

2. h(h(x))=h(x) $\forall$ x $\in$ M

3. h(xy)=h(x), ha x $\in$ M\K és h(y), ha x $\in$ K

4. t(xy)=t(x)y, ha x $\in$ M\K és t(y), ha x $\in$ K

Milyen esetben lesznek a h(x)=x tulajdonságú elemek felbonthatatlanok (esetleg prímek)?

Köszi

Károly

[5] Károly	2006-08-10 15:57:11
Nos, ha K-val jelöljük azokat az elemeket, amelyeknek (asszociált osztályokat számolva) pontosan két bontójuk van, és B-vel a monoid bázisát (egy olyan generátorrendszert, amelyből már nem lehet elemet elhagyni úgy, hogy generátorrendszer maradjon), akkor sejtésem szerint K=B=M=F. Mi a véleményetek?
Előzmény: [4] Károly, 2006-08-08 09:36:52

[4] Károly

2006-08-08 09:36:52

Ügyesek vagytok... Köszönöm.

És mi a véleményetek a bontók számáról...? :-)

Előzmény: [2] Károly, 2006-08-07 23:10:52

[3] 2501

2006-08-08 00:42:51

$A \subset B,~ A \matrix{{}_\frac{{}^\subset}{}} B$

\matrix{{}_\frac{{}^\subset}{}}

Jó játék, mindjárt nyitok TeX-hacker topikot.

Előzmény: [2] Károly, 2006-08-07 23:10:52

[2] Károly

2006-08-07 23:10:52

Egységelemes félcsoportban

(a) $\angle$ reflexív és tranzitív

(b) az asszociáltság ekvivalenciareláció

(d) a rendezés legkisebb (és ezért minimális) eleme az egységelem

(e) ha az egységelemet elhagyjuk, a keletkezett halmazban minimális elemek a felbonthatatlanok (a két halmaz azonos)

(f) ha P-vel jelöljük a prímeket, F-fel a felbonthatatlanokat és M-mel a minimális elemeket, akkor $P \matrix{{}_\frac{{}^\subset}{}} F = M$

(Nincs \subseteq!! Megőrülök... - Jó ötlet volt ez a hackerkedés, engedelmetekkel be is tettem a jelet ide. Sirpi)

Előzmény: [1] Károly, 2006-07-30 15:16:08

[1] Károly

2006-07-30 15:16:08

Monoidnak nevezek egy A×A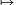 $\mapsto$ A művelettel ellátott algebrai struktúrát - minden egyéb követelmény nélkül. (Az újabb szóhasználat grupoidnak mondja, de én már öreg vagyok...:-))

Nevezzük "bontja" relációnak azt a relációt, amelyet a és b között azzal definiálunk, hogy a monoidban megoldható az ax=b egyenlet. (A monoid műveletét egyszerű egymásmelléírással jeöljük.) Ilyeneket mondunk: a bontja b-t, b bontható a-val vagy a bontója b-nek.

A "bontja" reláció jele legyen $\angle$ .

Ha a $\angle$ b és b $\angle$ a, akkor a-t és b-t asszociáltaknak nevezzük.

Egy p elemet prímnek nevezünk akkor, ha p $\angle$ ab $\implies$ (p $\angle$ a vagy p $\angle$ b).

Egy f elemet felbonthatatlannak nevezünk akkor, ha f=ab-ből az következik, hogy vagy f és a vagy f és b asszociáltak.

Mit mondhatunk az alábbiakról:

1. Mikor lesz a "bontja" reláció parciális rendezés? (1.a.) Mikor lesz legalább reflexív és tranzitív?

2. Mit mondhatunk az (1) alatti parciális rendezés minimális elemeiről? Mi közük van a prímekhez?

3. Mikor alkotnak a prímek generátorrendszert a monoidban?

4. Mi az összefüggés a prímtulajdonság és a bontók száma között?

5. Mi a viszony a prímek és a felbonthatalanok között?

Köszönettel

Károly

Már regisztráltál?
Új vendég vagy?