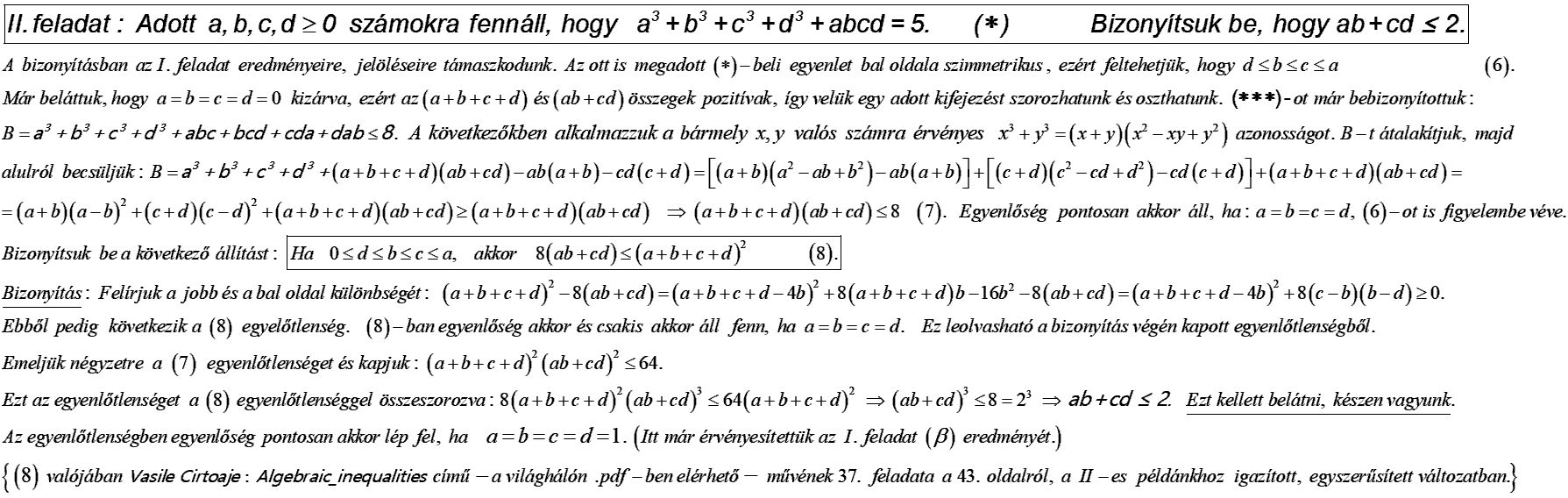Fórum: Nehezebb matematikai problémák

Ingyen letölthető Freud könyv, 2024-es kiadás 277. oldalán:

"9.5.1 Tétel (Hoffman–Singleton-tétel) Megjegyzés: Sokáig megoldatlan volt, hogy mi a helyzet d = 57-re. Végül 2020-ban igazolták, hogy nem létezik ilyen gráf."

Hm ez nagy eredmény, lenne. Találtam is egy 2020-as bizonyítás cáfolását: https://arxiv.org/abs/2210.09577, szóval a probléma még nagyon is él.

Jo regi ez a feladat is, de ime egy levezetes mindket verziora:

A gondolat eleg egyszeru: a feltetelunk baratsagtalabb mint a minimalizalando fuggvenyunk, szoval csereljuk meg a kettot es probaljunk valamifele dualis allitast belatni (szerintem eleg termeszetes otlet, az egyenlotlenseg 'szep' feluletek szintvonalainak a relaciojarol mond valamit ), majd ezt ugyesen alkalmazva probaljunk ellentmondasra jutni. Ez abszolut kozepiskolas (nincs benne derivalas sehol). A B.3989. feladat például ugyanígy belathato :)

Nezzuk a dualis allitast: \(\displaystyle a+b+c+d=4\Rightarrow a^{3}+b^{3}+c^{3}+d^{3}+abcd\geq5 \)

Ha barmelyik valtozo \(\displaystyle 0\), hatvanykozepekbol adodik:

\(\displaystyle 3\cdot\frac{a^{3}+b^{3}+c^{3}+d^{3}+abcd}{3}=3\cdot\frac{a^{3}+b^{3}+c^{3}}{3}\geq3\cdot\left(\frac{a+b+c}{3}\right)^{3}=3\cdot\left(\frac{a+b+c+d}{3}\right)^{3}=3\left(\frac{4}{3}\right)^{3}>5 \)

Ha \(\displaystyle 2-2\) valtozo egyenlo, legyen \(\displaystyle a=b=x\) es \(\displaystyle c=d=y\), ekkor \(\displaystyle x+y=2\), es legyen \(\displaystyle x=1+\alpha\) and \(\displaystyle y=1-\alpha\):

\(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd=2x^{3}+2y^{3}+x^{2}y^{2}= \)

\(\displaystyle =2(1-\alpha)^{3}+(\alpha+1)^{2}(1-\alpha)^{2}+2(\alpha+1)^{3}=\alpha^{4}+10\alpha^{2}+5\geq5 \)

Egyenloseg akkor es csak akkor ha \(\displaystyle \alpha=0\), i.e. \(\displaystyle a=b=c=d=1\).

Bevezetve a \(\displaystyle 2u=a+b\) es \(\displaystyle 2v=a-b\) valtozokat, szimmetria miatt felteheto \(\displaystyle a\geq b\):

\(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd=\frac{1}{4}(a+b)^{2}(a+b+cd)+\frac{1}{4}(a-b)^{2}(3(a+b)-cd)+c^{3}+d^{3} \)

Igy ha \(\displaystyle 3\left(a+b\right)\geq cd\), akkor \(\displaystyle p\left(a,b,c,d\right)=a^{3}+b^{3}+c^{3}+d^{3}+abcd\) novekszik fix \(\displaystyle a+b\) mellett a \(\displaystyle a-b\) valtozoban, kulonben csokken, igy:

\(\displaystyle p\left(a,b,c,d\right)\geq\min\left(p\left(\frac{a+b}{2},\frac{a+b}{2},c,d\right),p\left(a+b,0,c,d\right)\right) \)

Alkalmazzuk ezt parszor, felhasznalva, hogy \(\displaystyle 3\left(a+b\right)\geq cd\) ha \(\displaystyle cd=0\).

\(\displaystyle p\left(a,b,c,d\right)\geq\min\left(p\left(\frac{a+b}{2},\frac{a+b}{2},c,d\right),p\left(a+b,0,c,d\right)\right)\geq \)

\(\displaystyle \geq\min\left(p\left(\frac{a+b}{2},\frac{a+b}{2},\frac{c+d}{2},\frac{c+d}{2}\right),p\left(\frac{a+b}{2},\frac{a+b}{2},c+d,0\right),p\left(a+b,0,c,d\right)\right)= \)

\(\displaystyle =\min\left(p\left(\frac{a+b}{2},\frac{a+b}{2},\frac{c+d}{2},\frac{c+d}{2}\right),3\left(\frac{4}{3}\right)^{3},3\left(\frac{4}{3}\right)^{3}\right)\geq\min\left(5,3\left(\frac{4}{3}\right)^{3},3\left(\frac{4}{3}\right)^{3}\right)=5 \)

Egyenloseg \(\displaystyle a=b=c=d=1\) eseten. Most tegyuk fel, hogy valameny \(\displaystyle \lambda>0\)-ra teljesul \(\displaystyle a+b+c+d=4\left(1+\lambda\right)\), de ekkor \(\displaystyle \frac{a}{1+\lambda}+\frac{b}{1+\lambda}+\frac{c}{1+\lambda}+\frac{d}{1+\lambda}=4\), igy a dualis alapjan:

\(\displaystyle 5=a^{3}+b^{3}+c^{3}+d^{3}+abcd>\frac{a^{3}+b^{3}+c^{3}+d^{3}}{\left(1+\lambda\right)^{3}}+\frac{abcd}{\left(1+\lambda\right)^{4}}\geq5 \)

Ellentmondas, es keszen is vagyunk.

Szerintem tanulsagos ez az ut. Lojunk most az eredeti feladatra. Ebben van benne egy "vegyuk eszre, hogy" jellegu lepes, amit vegul is ki lehet talalni, de a szorzatta alakitas munkasabb.

\(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd=5\Rightarrow ab+cd\leq2\) ha \(\displaystyle a,b,c,d\) nemnegativak.

Perem tisztazasa: ha valamelyik valtozo \(\displaystyle 0\), akkor az allitas a hatvanykozep-egyelotlenseggel fel sorban kijön (\(\displaystyle 5 \geq 5-b^3=c^3+d^3\geq 2 (cd)^{3/2}\) miatt).

Pozitiv \(\displaystyle x,y\)-ra [homogenizalasbol es negyzetre emelesbol jonnek majd ezek, ha bevezeti az ember a \(\displaystyle 2p=(x+y)\) es \(\displaystyle 2q=x-y\) változokat akkor igazabol meg nemi szamolasbol ki is esik ez ]:

\(\displaystyle \frac{5}{4}\left(x^{2}+y^{2}\right)^{2}-x^{2}y^{2}=\frac{1}{4}\left(5x^{4}+6x^{2}y^{2}+5y^{4}\right)>0\)

\(\displaystyle 0\leq2\left(x^{2}+y^{2}\right)\left(x^{3}+y^{3}\right)^{2}-\left(\frac{5}{4}\left(x^{2}+y^{2}\right)^{2}-x^{2}y^{2}\right)^{2}=\)

\(\displaystyle =\frac{\left(x-y\right)^{2}}{16}\left[7(x-y)^{2}(x+y)^{2}\left(x^{2}+y^{2}\right)+2xy\left(7x^{4}+18x^{2}y^{2}+7y^{4}\right)\right] \)

Egyenloseg csak \(\displaystyle x=y\) eseten.

Nezzuk most a feladat dualisat: Ha \(\displaystyle ab+cd=2\), akkor \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd\geq5\), egyeloseg csak \(\displaystyle a=b=c=d=1\) eseten.

Legyen \(\displaystyle c\) es \(\displaystyle d\) fixalt, ekkor \(\displaystyle ab=v\)-t es \(\displaystyle u=\sqrt{\frac{a}{b}}\)-t bevezetve:

\(\displaystyle a^{3}+b^{3}=v\sqrt{v}\left(\left(u\sqrt{u}-\frac{1}{u\sqrt{u}}\right)^{2}+2\right)\geq 2v\sqrt{v}\)

Tehat ha \(\displaystyle a=b=\sqrt{v}\)-t valasztva a \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd\) kifejezest csokkentjuk, igy felteheto \(\displaystyle a=b=x\) es \(\displaystyle c=d=y\). Azt kellene tehat belatnunk, hogy \(\displaystyle x>0,y>0\)-ra

\(\displaystyle x^{2}+y^{2}=2\Rightarrow2x^{3}+2y^{3}\geq5-\left(x^{2}y^{2}\right)\)

Nyilvanvaloan:

\(\displaystyle x^{2}y^{2}\leq\left(\frac{x^{2}+y^{2}}{2}\right)^{2}=1\Rightarrow2x^{3}+2y^{3}-x^{2}y^{2}+5\geq2x^{3}+2y^{3}-1+5=2x^{3}+2y^{3}+4\geq4>0\)

\(\displaystyle 0\leq2\left(x^{2}+y^{2}\right)\left(x^{3}+y^{3}\right)^{2}-\left(\frac{5}{4}\left(x^{2}+y^{2}\right)^{2}-x^{2}y^{2}\right)^{2}=\)

\(\displaystyle =4\left(x^{3}+y^{3}\right)^{2}-\left(5-x^{2}y^{2}\right)^{2}=\left(2x^{3}+2y^{3}+x^{2}y^{2}-5\right)\left(2x^{3}+2y^{3}-x^{2}y^{2}+5\right) \)

De a masodik tenyezo pozitiv, szoval az elso nemnegativ, egyeloseg csak \(\displaystyle x=y=1\) esetben all, vagyis \(\displaystyle a=b=c=d=1\) eseten.

Vegul ha \(\displaystyle a^3+b^3+c^3+d^3+abcd=5\) es \(\displaystyle ab+cd=2\left(1+\lambda\right)\) teljesül valamely \(\displaystyle \lambda > 0\)-ra, akkor a valtozokat \(\displaystyle \frac{1}{\sqrt{1+\lambda}}\)-val osztva alkalmazhatjuk a masik iranyban kapott egyenlotlenseget, mikozben a kifejezes erteke csokken.

\(\displaystyle 5=a^{3}+b^{3}+c^{3}+d^{3}+abcd>\left(a'\right)^{3}+\left(b'\right)^{3}+\left(c'\right)^{3}+\left(d'\right)^{3}+a'b'c'd'= \)

\(\displaystyle =\frac{a^{3}+b^{3}+c^{3}+d^{3}}{\sqrt{\left(1+\lambda\right)^{3}}}+\frac{abcd}{\left(1+\lambda\right)^{2}}\geq5\)

ellentmondas, egyelotlenseg belatva.

Elnézést a nem tökéletes ábráért, a lényeg azért látszik rajta.

RE: 3. eset: Ilyenkor második közös pontról nem lehet beszélni...

Mivel az első két esetben az \(\displaystyle OO_1\) egyenes és egy hiperbola pont ( \(\displaystyle O_2\) ) viszonyáról van szó, a harmadik esetben kitűzhetjük feladatul az \(\displaystyle OO_1\) egyenes és a három hiperbola egy-egy aszimptotája irányának vizsgálatát.

1. eset:

Ha az inverzió középpontja a \(\displaystyle K\) kör belsejében van, akkor az inverz képe (legyen \(\displaystyle K'\)) egy olyan kör lesz, amelyik a belsejében tartalmazza a \(\displaystyle K_A\), \(\displaystyle K_B\) és \(\displaystyle K_C\) köröket, amelyeket érint. Jelöljük \(\displaystyle K'\) sugarának a hosszát \(\displaystyle R\)-rel, középpontját \(\displaystyle O_2\)-vel. Ekkor

\(\displaystyle \mathcal{ d }_A(O_2)=R-r_A \)

\(\displaystyle \mathcal{ d }_B(O_2)=R-r_B \)

\(\displaystyle \mathcal{ d }_C(O_2)=R-r_C \)

és ezért

\(\displaystyle \mathcal{ d }_B(O_2)-\mathcal{ d }_A(O_2)=r_A-r_B=b-a \)

de mivel

\(\displaystyle \mathcal{ d }_B(P)-\mathcal{ d }_A(P)=b-a \)

jellemzi a (3) hiperbolaág társát, ezért \(\displaystyle O_2\) rajta van a \(\displaystyle C\) csúcson áthaladó hiperbolaág társán. Hasonlóan látható be, hogy rajta van a másik két hiperbolaág társán is, tehát ez lesz a három (társ) hiperbolaág közös pontja. Ebben az esetben az inverzió középpontja, ami a beírható kör középpontja az \(\displaystyle O_1O_2\) szakaszra esik (az inverzió tulajdonsága).

2. eset:

Ha az inverzió középpontja a \(\displaystyle K\) körön kívül van, akkor az inverz képe (legyen \(\displaystyle K'\)) egy olyan kör lesz, amelyik nem tartalmazza a \(\displaystyle K_A\), \(\displaystyle K_B\) és \(\displaystyle K_C\) köröket, amelyeket érint. Jelöljük \(\displaystyle K'\) sugarának a hosszát \(\displaystyle R\)-rel, középpontját \(\displaystyle O_2\)-vel. Ekkor

\(\displaystyle \mathcal{ d }_A(O_2)=R+r_A \)

\(\displaystyle \mathcal{ d }_B(O_2)=R+r_B \)

\(\displaystyle \mathcal{ d }_C(O_2)=R+r_C \)

és ezért

\(\displaystyle \mathcal{ d }_A(O_2)-\mathcal{ d }_B(O_2)=r_A-r_B=b-a \)

tehát \(\displaystyle O_2\) rajta van a \(\displaystyle C\) csúcson áthaladó (3) hiperbolaágon. Hasonlóan látható be, hogy rajta van a másik két hiperbolaágon is, tehát ez lesz a három (elsődleges) hiperbolaág másik közös pontja. Ebben az esetben az inverzió középpontja, ami a beírható kör középpontja az \(\displaystyle O_1O_2\) szakaszon kívülre esik az \(\displaystyle O_1O_2\) egyenesen (az inverzió tulajdonsága).

3. eset:

Ha az inverzió középpontja a \(\displaystyle K\) kör kerületére esik, akkor \(\displaystyle K\) inverz képe egy egyenes lesz, ami persze érinti a \(\displaystyle K_A\), \(\displaystyle K_B\) és \(\displaystyle K_C\) köröket. Ilyenkor második közös pontról nem lehet beszélni, mert az egyet jelentene egy második érintő körrel. Mint azt Pythagoras-tétellel könnyű igazolni, ebben az esetben áll fenn a

\(\displaystyle r_C=\frac{r_A*r_B}{(\sqrt{r_A} + \sqrt{r_B})^2} \tag{ 4 } \)

összefüggés. Így a legkisebb kör sugarának a viszonya a másik két sugárhoz dönti el, hogy a 3 eset közül melyik teljesül:

\(\displaystyle r_C>\frac{r_A*r_B}{(\sqrt{r_A} + \sqrt{r_B})^2} \)

az 1. eset,

\(\displaystyle r_C<\frac{r_A*r_B}{(\sqrt{r_A} + \sqrt{r_B})^2} \)

a 2. eset.

Csak megjegyezzük, hogy a (4) egyenlőség írható az alábbi, könnyebben megjegyezhető formában is:

\(\displaystyle \frac{1}{\sqrt{r_C}}=\frac{1}{\sqrt{r_A}} + \frac{1}{\sqrt{r_B}} \)

vagy visszavezetve a háromszög oldalaira:

\(\displaystyle \frac{1}{\sqrt{s-c}}=\frac{1}{\sqrt{s-a}} + \frac{1}{\sqrt{s-b}} \)

Megköszönve Sinobi hozzászólását és sakkmath értékes észrevézelét, úgy gondolom, hogy most már teljes bizonyítást tudok küldeni (méret túllépés miatt 2 darabban).

Használjuk a [851] jelöléseit:

Jelöljük a háromszög csúcsait a szokásnak megfelelően \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\)-vel! \(\displaystyle A\)-val szemben legyen a legrövidebb, \(\displaystyle C\)-vel szemben a leghosszabb oldal. Az oldalak hossza legyen rendre \(\displaystyle a<b<c\), a háromszög fél kerületét a szokásoknak megfelelően jelöljük \(\displaystyle s\)-sel! Jelölje \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\) a megfelelő csúccsal szemközti oldalon a beírható kör érintési pontját! Legyen továbbá \(\displaystyle r_A\) az \(\displaystyle AB_1\) és \(\displaystyle AC_1\) szakaszok, \(\displaystyle r_B\) a \(\displaystyle BA_1\) és \(\displaystyle BC_1\) szakaszok, \(\displaystyle r_C\) pedig a \(\displaystyle CA_1\) és \(\displaystyle CB_1\) szakaszok hossza! Vezessük be még az \(\displaystyle A\) pont körül \(\displaystyle r_A\) sugárral rajzolt körre a \(\displaystyle K_A\), a \(\displaystyle B\) pont körül \(\displaystyle r_B\) sugárral rajzolt körre a \(\displaystyle K_B\) és a \(\displaystyle C\) pont körül \(\displaystyle r_C\) sugárral rajzolt körre a \(\displaystyle K_C\) jelölést.

Definiáljunk három függvényt: \(\displaystyle \mathcal{ d }_A(P)\) jelölje a sík tetszőleges \(\displaystyle P\) pontjának a távolságát \(\displaystyle A\)-tól, \(\displaystyle \mathcal{ d }_B(P)\) jelölje a sík tetszőleges \(\displaystyle P\) pontjának a távolságát \(\displaystyle B\)-től és \(\displaystyle \mathcal{ d }_C(P)\) jelölje a sík tetszőleges \(\displaystyle P\) pontjának a távolságát \(\displaystyle C\)-től.

Az \(\displaystyle A\) ponton átmenő hiperbolaágat azon \(\displaystyle P\) pontok alkotják, amelyekre

\(\displaystyle \mathcal{ d }_B(P)-\mathcal{ d }_C(P)=c-b \tag{ 1 } \)

A \(\displaystyle B\) ponton átmenő hiperbolaágat azon \(\displaystyle P\) pontok alkotják, amelyekre

\(\displaystyle \mathcal{ d }_A(P)-\mathcal{ d }_C(P)=c-a \tag{ 2 } \)

Végül a \(\displaystyle C\) ponton átmenő hiperbolaágat azon \(\displaystyle P\) pontok alkotják, amelyekre

\(\displaystyle \mathcal{ d }_A(P)-\mathcal{ d }_B(P)=b-a \tag{ 3 } \)

Vegyük észre, hogy ha egy \(\displaystyle P\) pont eleget tesz (1)-nek és (2)-nek is (rajta van mindkét hiperbolaágon), akkor eleget tesz (3)-nak is, hiszen csak ki kell vonni egymásból a két egyenlet megfelelő oldalait, (2)-ből az (1)-et és megkapjuk (3)-at (azaz a pont rajta van a harmadik hiperbolaágon is).

Mivel \(\displaystyle r_C=s-c\) és \(\displaystyle r_B=s-b\), ezért

\(\displaystyle \mathcal{ d }_B(A_1)-\mathcal{ d }_C(A_1)=r_B-r_C = (s-b)-(s-c)=c-b \)

és így \(\displaystyle A_1\) rajta van az \(\displaystyle A\) ponton átmenő hiperbolaágon és mivel a hiperbola fókuszait összekötő szakaszon is rajta van, ezért \(\displaystyle A_1\) az \(\displaystyle A\) ponton átmenő hiperbolaág csúcsa.

Ehhez hasonlóan \(\displaystyle B_1\) rajta van a \(\displaystyle B\) ponton átmenő hiperbolaágon és mivel a hiperbola fókuszait összekötő szakaszon is rajta van, ezért \(\displaystyle B_1\) a \(\displaystyle B\) ponton átmenő hiperbolaág csúcsa. Ugyanígy \(\displaystyle C_1\) rajta van a \(\displaystyle C\) ponton átmenő hiperbolaágon és mivel a hiperbola fókuszait összekötő szakaszon is rajta van, ezért \(\displaystyle C_1\) a \(\displaystyle C\) ponton átmenő hiperbolaág csúcsa.

Mivel az \(\displaystyle A\) ponttól az \(\displaystyle A_1\)-ig tartó hiperboladarab teljes egészében az \(\displaystyle ABC\triangle\) belsejében halad és elválasztja egymástól a \(\displaystyle B\) és \(\displaystyle B_1\) pontokat, ezért a \(\displaystyle B\) ponttól az \(\displaystyle B_1\)-ig tartó hiperboladarabbal metszik egymást. A metszéspont legyen \(\displaystyle O=O_1\). Láttuk, hogy ha egy pont rajta van két hiperbolaágon, akkor rajta van a harmadikon is, tehát \(\displaystyle O_1\) a három hiperbolaág közös pontja, ami mindig létezik (ha \(\displaystyle a<b<c\)).

Legyen \(\displaystyle x_A\) az \(\displaystyle O_1\) pont távolsága a \(\displaystyle K_A\) körtől, és legyen \(\displaystyle x_B\) az \(\displaystyle O_1\) pont távolsága a \(\displaystyle K_B\) körtől! Ekkor egyrészt, mivel \(\displaystyle O_1\) rajta van a \(\displaystyle C\) ponton áthaladó hiperbolaágon, ezért

\(\displaystyle \mathcal{ d }_A(O_1)-\mathcal{ d }_B(O_1)=b-a \)

másrészt, mivel \(\displaystyle \mathcal{ d }_A(O_1)=r_A+x_A\) és \(\displaystyle \mathcal{ d }_B(O_1)=r_B+x_B\) és \(\displaystyle r_A-r_B=b-a\) ezért

\(\displaystyle \mathcal{ d }_A(O_1)-\mathcal{ d }_B(O_1)=(r_A+x_A)-(r_B+x_B)=b-a + (x_A-x_B) \)

így \(\displaystyle x_A-x_B=0\), azaz az \(\displaystyle O_1\) pont egyenlő távolságra van a \(\displaystyle K_A\) és \(\displaystyle K_B\) köröktől, hasonlóan látható be, hogy ugyanekkora távolságra van a \(\displaystyle K_C\) körtől is, tehát \(\displaystyle O_1\) egy olyan \(\displaystyle K\) körnek a középpontja, amelyik érinti a \(\displaystyle K_A\), \(\displaystyle K_B\) és \(\displaystyle K_C\) körök mindegyikét és természetesen az \(\displaystyle ABC\triangle\) beírható körének a belsejében helyezkedik el.

Invertáljuk a köröket az \(\displaystyle ABC\triangle\) beírható körére, mint az inverzió alapkörére vonatkozóan! Mivel a \(\displaystyle K_A\), \(\displaystyle K_B\) és \(\displaystyle K_C\) körök az inverzió alapkörét merőlegesen metszik, ezért ezek önmaguk képei lesznek. Mivel pedig az inverzió az érintést megtartja, ezért 3 esetet különböztethetünk meg: (folyt. köv.)

Legyen A,B,e, két pont, és egy egyenes rögzített a síkon.
Legyen \(\displaystyle h(P) := AP^2 - BP^2\), egy \(\displaystyle R^2 \to R\) függvény, amely a sík minden P pontjához hozzárendeli az A és B pontoktól vet távolságok négyzetének a különbségét.
A h függvény a \(\displaystyle P:(x,y)\) pont függvényében kifejtve: \(\displaystyle h(P) = (x - a_x)^2 + (y - a_y)^2 - (x - b_x)^2 + (y - b_y)^2 = 2x(b_x - a_x) + 2y(b_y-a_y) + a_x^2 + a_y^2 - b_x^2 -b_y^2\), elsőfokú kifejezés x-ben és y-ban, vagyis h(P) gráfja az \(\displaystyle R^3\) térben egy sík. (A és B rögzítettek.)
Ha ezt a h(P) függvényt csak az e egyenesen nézzük, akkor a gráfja egy lineáris függvény lesz. Azaz ha adott az e egyenesen 3 pont, D,K,L, akkor \(\displaystyle \frac{h(D)-h(K)}{DK} = \frac{h(K)-h(L)}{KL}\). És hasonlóan, a h lineáris függvény értékeinek az arányából ki lehet számolni a D,K,L pontok távolságainak az arányát.

\(\displaystyle D_B\) helyett általában \(\displaystyle D_A\)-nak kéne állnia.

Ne haragudj Sinobi, de a lemmádat és a bizonyítását sem értem. Légy szíves kicsit részletezni! A továbbiak olvasását néhány elírás nehezíti.

Amúgy, ha jól nézem, ezek a pontok Soddy pontok néven futnak, és az egyenes a Soddy line. És ezek a hiperbolák is az ő nevét viselik, legalábbis Kimberlingnél.
https://en.wikipedia.org/wiki/Frederick_Soddy

Diszkusszió nélkül, a [850]-es speciális esetre a megoldásom.

lemma: Ha adott a síkon két, A,B pont, és egy e egyenes, akkor ha az E pont végigfut az e egyenesen, akkor az \(\displaystyle AE^2 - BE^2 \) érték lineárisan változik.
Valóban, ez az érték az egész síkon lineáris (E függvényében a térben egy sík), és ez megszorítva az e egyenesre lineáris marad.

Innentől azt fogom igazolni, hogy a háromszög csúcsaiba rakott, beírt körre merőleges \(\displaystyle C_A, C_B, C_C\) körök páronkénti hatványvonalai ugyanott metszik az LK egyenest.

Legyen \(\displaystyle D_A\) az a pont, ahol a \(\displaystyle C_B, C_C\) körök hatványvonala metszi az LK egyenest, s.í.t, ciklikusan. A lemma miatt elég megmutatnom, hogy a

\(\displaystyle \frac{LD_A}{KD_A} = \frac{(BL^2-CL^2)-(BD_B^2-CD_B^2)}{(BK^2-CK^2)-(BD_B^2-CD_B^2)}\)

érték fix, nem változik az A,B,C ciklikus permutációjakor, azaz \(\displaystyle (D_A,K,L) = (D_B,K,L) = (D_C,K,L)\). (Szerintem ebből nem csak a szakaszok nagysága adódik, hanem hogy ugyanolyan irányba esik \(\displaystyle D_A,D_B,D_C\).)

Legyenek a körök sugarai \(\displaystyle r_A,r_B,r_C\). Mivel L a hiperbolák metszéspontja, így az AL,BL,CL távolságok ezeknek egy l-el való eltoltja (páronkénti különbségeik megegyeznek), \(\displaystyle AL,BL,CL = l+r_A, l+r_B, l+r_C\), és K-ra ugyanez: \(\displaystyle AK,BK,CK = k+r_A, k+r_B, l+k_C\).

Mivel \(\displaystyle D_A\) rajta van a B, C középpontú, érintkező körök hatványvonalán így \(\displaystyle (BD_B^2-CD_B^2) = r_B^2 - r_C^2\), ciklikusan.

Ezt beírva a fenti képletbe,

\(\displaystyle \frac{(BL^2-CL^2)-(BD_B^2-CD_B^2)}{(BK^2-CK^2)-(BD_B^2-CD_B^2)} = \frac{(r_B-r_C)(2l + r_B+r_C) - (r_B-r_C)( r_B+r_C)}{ (r_B-r_C)(2k + r_B+r_C) - (r_B-r_C)( r_B+r_C)} = \frac{l}{k}\)

adódik, ami valóban független az indextől. (És ezzel azt is kiszámoltuk, hogy hol van a D pont az LK egyenesen.)

Ismét megköszönöm sakkmath fontos észrevételét, aminek alapján a feladatot az alábbiak szerint pontosítom:

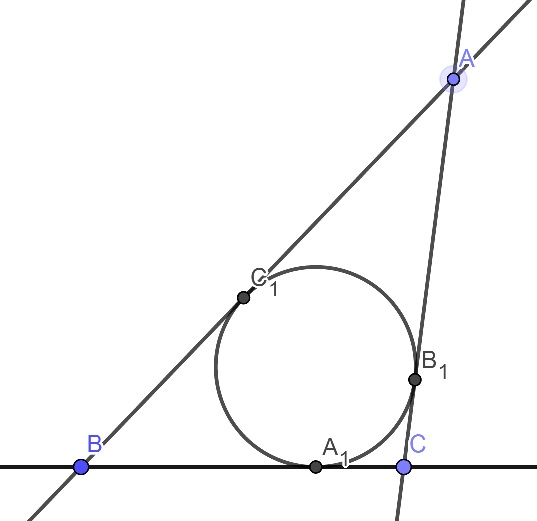
Legyen adott egy háromszög, amelynek oldalai különböző hosszúságúak! Minden csúcshoz rendeljük hozzá azt a fél hiperbolát (hiperbola ágat), amelyik átmegy a csúcson és fókuszpontjai a másik két csúccsal egyeznek meg! Bizonyítsuk be, hogy a három hiperbolaágnak van egy közös pontja!

Következzék a feladat további részének pontosítása:

Jelöljük a háromszög csúcsait a szokásnak megfelelően \(\displaystyle A\), \(\displaystyle B\) és \(\displaystyle C\)-vel! \(\displaystyle A\)-val szemben legyen a legrövidebb, \(\displaystyle C\)-vel szemben a leghosszabb oldal. Jelölje \(\displaystyle A_1\), \(\displaystyle B_1\) és \(\displaystyle C_1\) a megfelelő csúccsal szemközti oldalon a beírható kör érintési pontját! Legyen továbbá \(\displaystyle r_A\) az \(\displaystyle AB_1\) és \(\displaystyle AC_1\) szakaszok, \(\displaystyle r_B\) a \(\displaystyle BA_1\) és \(\displaystyle BC_1\) szakaszok, \(\displaystyle r_C\) pedig a \(\displaystyle CA_1\) és \(\displaystyle CB_1\) szakaszok hossza!

Ha

\(\displaystyle r_C<\frac{r_A*r_B}{(\sqrt{r_A} + \sqrt{r_B})^2} \)

akkor bizonyítsuk be, hogy ezeknek a hiperbola ágaknak van még egy - az előzőtől különböző - közös pontjuk! Bizonyítsuk be továbbá, hogy a háromszög beírható körének középpontja a két közös pontot összekötő egyenesre esik, de nem lesz a szakasz pontja!

Ha

\(\displaystyle r_C>\frac{r_A*r_B}{(\sqrt{r_A} + \sqrt{r_B})^2} \)

akkor tekintsük a hiperbolák másik ágát és bizonyítsuk be, hogy ezeknek is van egy közös pontjuk! Bizonyítsuk be továbbá, hogy a háromszög beírható körének középpontja a két közös pontot összekötő szakaszra esik!

Végül, ha

\(\displaystyle r_C=\frac{r_A*r_B}{(\sqrt{r_A} + \sqrt{r_B})^2} \)

akkor bizonyítsuk be, hogy nem létezik újabb közös pont.

A jelölések egyértelműsítése miatt közlöm az alábbi ábrát:

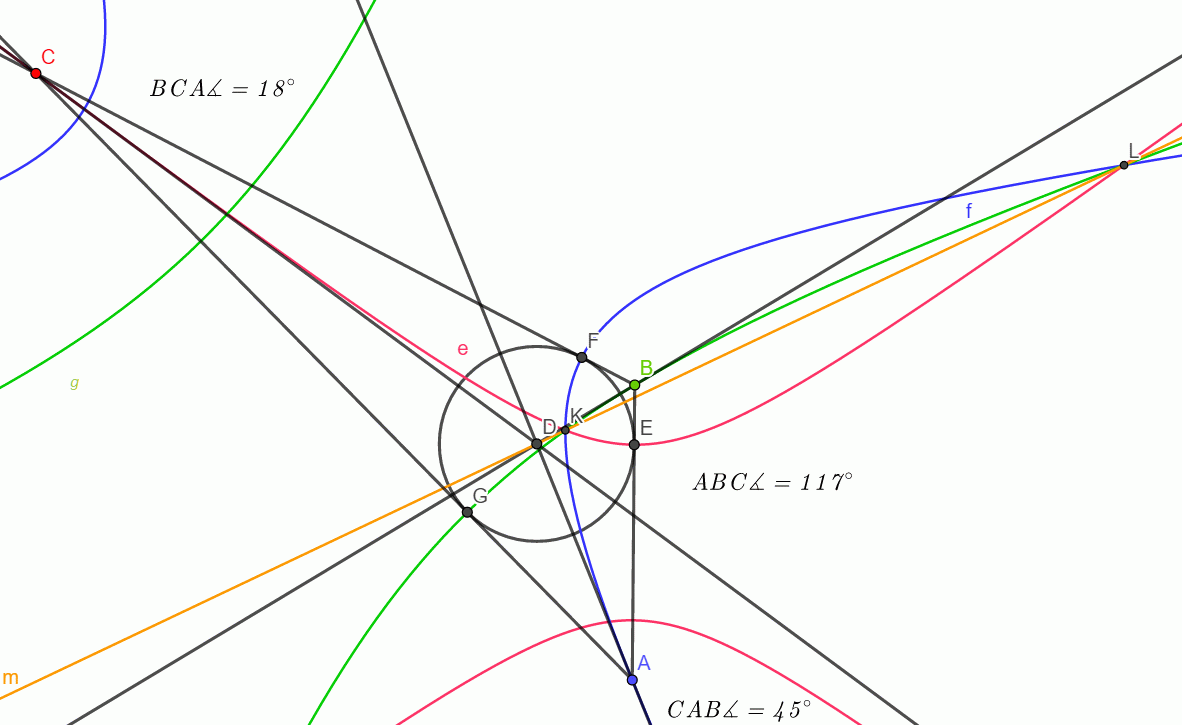
A szerkesztéshez a GeoGebra Classic 6 freeware programot használtam, melyet innen töltöttem le: www.geogebra.org/download?lang=hu.

Legyenek a háromszög szögei \(\displaystyle {45°, 117°, 18°}\). A \(\displaystyle D\)-középpontú beírt kör az \(\displaystyle {AB, BC, CA}\) oldalakat rendre az \(\displaystyle {E, F, G}\) pontokban érinti. Az \(\displaystyle {A, B, C}\) csúcsokon áthaladó \(\displaystyle {f, g, e}\) hiperbolákat rendre kék, zöld és (pirosas) püspöklila színek jelölik. A háromszögcsúcsokon áthaladó hiperbolaágak a \(\displaystyle K\) és \(\displaystyle L\) pontokban metszik egymást úgy, hogy a rajtuk átfektetett sárga színű egyenes – az ábra tanúsága szerint – áthalad a \(\displaystyle D\) ponton, miközben \(\displaystyle D\) nem pontja a \(\displaystyle KL\) szakasznak. Ha a program “kicsinyítés”- gombjának többszöri lenyomásával fokozatosan távolodunk a “rajzlaptól”, egyre erősebb a meggyőződésünk, hogy a csúcsokon át nem haladó hiperbolaágaknak nincs közös pontja. (Az ábráról egyébként újabb sejtések is leolvashatók.)

Köszönöm a helyesbítést, utána járok. Esetleg tudnál példákat küldeni az általad talált esetekre? Egyelőre nem tudom, hogy mi kerülte el a figyelmemet. Érdekelne a dinamikus szerkesztő programod is. Hozzáférhető?

Egyelőre csak dinamikus szerkesztőprogrammal vizsgálgattam a feladat különböző eseteit. Feltételezve, hogy e program nem csal, pusztán a látottakra támaszkodva, két állításodat is problematikusnak tartom.

Az egyik mondatod:

"Most tekintsük a hiperbolák másik ágát és bizonyítsuk be, hogy ezeknek is van egy közös pontjuk!"

Ez az állítás bizonyos háromszögekre igaz, ám találtam olyan háromszögeket is, ahol a másik hiperbolaágak nem konkurensek! Ilyenkor is létezett második közös pont, de ez az első ágak újabb közös pontjaként jött létre.

Feladatkitűzésed záró mondata:

"Bizonyítsuk be, hogy a háromszög beírható körének középpontja a két közös pontot összekötő szakaszra esik!"

Itt ezt a befejezést tartom jónak: (...) a két közös pontot összekötő egyenesre esik.

Indoklás az utóbbihoz: a szerkesztőprogrammal előállíthatók olyan háromszögek is, melyeknél a beírható kör középpontja nem esik a szóban forgó szakasz belsejébe.

Legyen adott egy háromszög, amelynek oldalai különböző hosszúságúak! Minden csúcshoz rendeljük hozzá azt a fél hiperbolát (hiperbola ágat), amelyik átmegy a csúcson és fókuszpontjai a másik két csúccsal egyeznek meg! Bizonyítsuk be, hogy a három hiperbolaágnak van egy közös pontja! Most tekintsük a hiperbolák másik ágát és bizonyítsuk be, hogy ezeknek is van egy közös pontjuk! Bizonyítsuk be, hogy a háromszög beírható körének középpontja a két közös pontot összekötő szakaszra esik!

Találtam egy elütést.

Téves kifejezés: \(\displaystyle -a(b+b+c)\). Javítása: \(\displaystyle -a(b+c+d)\).

(Javított és újratördelt változat.)

A [833]-as hozzászólásban megismert két feladat után következzék a Berkó Erzsébet által felfedezett, kapcsolódó, III. probléma megoldása – középiskolás módszerekkel.
III. feladat: Adott \(\displaystyle a, b, c, d\ge0\) számokra fennáll, hogy \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd=5\) \(\displaystyle (\ast).\)
Bizonyítsuk be, hogy \(\displaystyle a+b+c+d\le4\).
Megoldás: A \(\displaystyle (\ast)\) egyenlet bal oldala szimmetrikus, ezért feltehetjük, hogy \(\displaystyle d\le{b}\le{c}\le{a}\).
Tegyük fel, hogy: \(\displaystyle {a}>{\root 3\of {5}}\). Ekkor \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd>5\), ami ellentmond \(\displaystyle (\ast)\)-nak. Most tegyük fel, hogy \(\displaystyle a<1\). Ekkor \(\displaystyle d^{3},b^{3},c^{3},a^3,abcd<1\) következtében \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd<5\) adódna, ami szintén ellentmondás \(\displaystyle (\ast)\)-ra nézve. Beláttuk tehát, hogy \(\displaystyle 1\le{a}\le{\root 3\of {5}}\). A \(\displaystyle {\bf (*)}\) feltételből az is következik, hogy \(\displaystyle {a}={\root 3\of {5}}\) akkor és csakis akkor igaz, ha \(\displaystyle d=b=c=0\).

Nem állhat fenn \(\displaystyle d>1\) sem: ha \(\displaystyle d>1\) lenne, akkor \(\displaystyle d^{3},b^{3},c^{3},a^3,abcd>1\) következne, ez pedig az \(\displaystyle a^{3}+b^{3}+c^{3}+d^{3}+abcd>5\) ellentmondáshoz vezetne. Ezzel igazoltuk, hogy \(\displaystyle 0\le{d}\le{1}\). Az eddigiek ismeretében vizsgáljuk meg, hol tartózkodhat az 1-es szám az \(\displaystyle a,b,c,d\) számok sorrendjéhez viszonyítva. Nem lehet \(\displaystyle d>1\) és nem lehet \(\displaystyle a<1,\) ezért csak e három eset fordulhat elő:

\(\displaystyle 1): 0\le{d}\le{1}\le{b}\le{c}\le{a}\)
2): \(\displaystyle 0\le{d}\le{b}\le{1}\le{c}\le{a}\)
3): \(\displaystyle 0\le{d}\le{b}\le{c}\le{1}\le{a}.\)
Mindhárom elrendezésben legyen \(\displaystyle T=4-(a+b+c+d).\) Be kell bizonyítani, hogy \(\displaystyle T\ge0.\)

1) eset: \(\displaystyle 0\le{d}\le{1}\le{b}\le{c}\le{a}.\) Alkalmazzuk a következő helyettesítéseket:

\(\displaystyle d=1-x,b=y+1,c=v+1,a=z+1,\) ahol \(\displaystyle 0\le{x}\le{1}\) és \(\displaystyle y,v,z\ge0\).

A behelyettesítések után a bizonyítandó \(\displaystyle T\ge0\) egyenlőtlenség megfelelője ez lesz: \(\displaystyle T_{1}=x-(y+v+z)\ge0,\) a \(\displaystyle (\ast)\) feltétel pedig így alakul:
\(\displaystyle 0=a^{3}+b^{3}+c^{3}+d^{3}+abcd-5\Longrightarrow\)

\(\displaystyle 0=y^{3}+v^{3}+z^{3}-x^{3}+3(x^{2}+y^{2}+v^{2}+z^{2})+(yvz-xyvz)+(yv-xyv)+\)

\(\displaystyle (vz-vzx)+(yz-xyz)-(xy+xv+xz)+4(y+v+z-x)=\)

\(\displaystyle 4(y+v+z-x)-x(y+v+z)+(1-x)[yvz+yv+vz+zy]+y^{3}+v^{3}+z^{3}+\)

\(\displaystyle [x^{2}-x^{3}]+2x^{2}+3(y^{2}+v^{2}+z^{2})=4(y+v+z-x)+x^{2}+\)

\(\displaystyle [x^{2}-x(y+v+z)]+(1-x)(yvz+yv+vz+zy)+x^{2}(1-x)+y^{3}+v^{3}+z^{3}+\)

\(\displaystyle 3(y^{2}+v^{2}+z^{2})\Leftrightarrow\\ 4[x-(y+v+z)]-x[x-(y+v+z)]=\)

\(\displaystyle (1-x)(x^{2}+yvz+yv+vz+zy)+x^{2}+y^{3}+v^{3}+z^{3}+3(y^{2}+v^{2}+z^{2})\Leftrightarrow\)

\(\displaystyle (4-x)[x-(y+v+z)]=(1-x)(x^{2}+yvz+yv+vz+zy)+x^{2}+y^{3}+v^{3}+\)

\(\displaystyle z^{3}+3(y^{2}+v^{2}+z^{2})\; {(**)}.\)

Mivel \(\displaystyle x,y,v,z\ge0\) és \(\displaystyle 4-x>1-x=d\ge{0},\) következik, hogy az utóbbi, \(\displaystyle {\bf(**)}\) egyenlet jobb oldalán nemnegatív kifejezés áll. Ez azt jelenti, hogy a bal oldalán is nemnegatív kifejezésnek kell állnia. Mindent összevetve adódik, hogy \(\displaystyle T_{1}=x-(y+v+z)\ge0,\) amit bizonyítani kellett.

2) eset: \(\displaystyle 0\le{d}\le{b}\le{1}\le{c}\le{a}.\) Alkalmazzuk a következő helyettesítéseket:

\(\displaystyle d=1-x,b=1-y,c=v+1,a=z+1,\) ahol \(\displaystyle 0\le{x,y}\le{1}\) és \(\displaystyle v,z\ge0\).

A behelyettesítések után a bizonyítandó \(\displaystyle T\ge0\)

egyenlőtlenség megfelelője ez lesz: \(\displaystyle T_{2}=x+y-(v+z)\ge0,\) a \(\displaystyle (\ast)\) feltétel pedig így alakul:
\(\displaystyle 0=a^{3}+b^{3}+c^{3}+d^{3}+abcd-5\Longrightarrow\)

\(\displaystyle 0=v^{3}+z^{3}-(x^{3}+y^{3})+3(x^{2}+y^{2}+v^{2}+z^{2})-[v(x+y)+z(x+y)]+\)

\(\displaystyle [2vz-vz(x+y)]-vz+4[v+z-(x+y)]+[xy(v+1)+xyz(v+1)]=\)

\(\displaystyle -(x+y)(v+z)+vz[2-(x+y)]+2[(x-y)^{2}+xy]+[2xy+x^{2}+y^{2}]+\)

\(\displaystyle 4[v+z-(x+y)]+v^{3}+z^{3}-(x^{3}+y^{3})-vz+3[(v-z)^{2}+2vz]+\)

\(\displaystyle xy(v+1)(z+1)\Leftrightarrow4[x+y-(v+z)]=[(x+y)^{2}-(x+y)(v+z)]-\)

\(\displaystyle (x+y)[(x-y)^{2}+xy]+2[(x-y)^{2}+xy]+vz[2-(x+y)]+xy(v+1)(z+1)\)

\(\displaystyle +v^{3}+z^{3}+3(v-z)^{2}+5vz\Leftrightarrow(x+y)[v+z-(x+y)]+4[x+y-(v+z)]=\)

\(\displaystyle [(x-y)^{2}+xy][2-(x+y)]+vz[2-(x+y)]+xy(v+1)(z+1)+v^{3}+z^{3}+\)

\(\displaystyle 3(v-z)^{2}+5vz\Leftrightarrow\)

\(\displaystyle [4-(x+y)][x+y-(v+z)]=[2-(x+y)][(x-y)^{2}+xy+vz]+\)

\(\displaystyle xy(v+1)(z+1)+v^{3}+z^{3}+3(v-z)^{2}+5vz\;(***)\).

Mivel \(\displaystyle x,y,v,z\ge0\) és \(\displaystyle 4-(x+y)>2-(x+y)=(1-x)+(1-y)=d+b\ge{0},\) következik, hogy a \(\displaystyle {\bf(***)}\) egyenletben, az egyenlőségjeltől jobbra nemnegatív kifejezés áll. Ez azt jelenti, hogy a bal oldalon is nemnegatív kifejezést kell találnunk. Mindent összevetve azt kaptuk, hogy \(\displaystyle T_{2}=x+y-(v+z)\ge0.\) Ezt kellett bizonyítani.

3) eset: \(\displaystyle 0\le{d}\le{b}\le{c}\le{1}\le{a}.\) Alkalmazzuk a következő helyettesítéseket:

\(\displaystyle d=1-x,b=1-y,c=1-v,\) ahol \(\displaystyle 0\le{x,y,v}\le{1}.\)

Az 1. esetben a \(\displaystyle {\bf (**)}\) egyenlet bal oldalán a \(\displaystyle T_{1}\) kifejezés szorzója \(\displaystyle P_{1}=4-x.\) A 2. esetben a \(\displaystyle {\bf (***)}\) egyenlet bal oldalán a \(\displaystyle T_{2}\) kifejezés szorzója \(\displaystyle P_{2}=4-(x+y).\) Ezekből megsejthető a képzési szabály, mely szerint a 3. esetben alkalmazható \(\displaystyle P_{3}\) szorzó \(\displaystyle P_{3}=4-(x+y+v)\) lehet. Itt, a 3. esetben a \(\displaystyle P_{3}\) kifejezés \(\displaystyle (b,c,d)\)-változós alakját használjuk:
\(\displaystyle P_{3}=4-(x+y+v)=1+(1-x)+(1-y)+(1-v)={\bf b+c+d+1}.\)
Legyen \(\displaystyle Q=P_{3}T=(b+c+d+1)[4-(a+b+c+d)].\) \(\displaystyle P_{3}>0\) miatt a \(\displaystyle T\ge0\) egyenlőtlenség pontosan akkor teljesül, ha \(\displaystyle Q\ge0.\) Állításunk: \(\displaystyle Q\ge0.\) Indirekt bizonyítással folytatjuk: feltesszük, hogy \(\displaystyle Q<0\), azaz \(\displaystyle Q=(b+c+d+1)[4-(a+b+c+d)]<0 \Leftrightarrow\)

\(\displaystyle 3b+3c+3d-ba-ca-da-b^{2}-2bc-2bd-c^{2}-2cd-d^{2}-a+4<0\)

\(\displaystyle \Leftrightarrow\)

\(\displaystyle 4-a+3(b+c+d)-a(b+b+c)-[b^{2}+c^{2}+d^{2}+2(bc+cd+db)]<0\)

\(\displaystyle \Leftrightarrow\)

\(\displaystyle (b+c+d)^{2}+(a-3)(b+c+d)+a-4>0.\)

Vezessük be az \(\displaystyle s=b+c+d\) új változót, ahol \(\displaystyle 0\le{s}\le{3}\). Ekkor legutóbbi egyenlőtlenségünk az \(\displaystyle s^{2}+(a-3)s+a-4>0\) alakot ölti, ahol az \(\displaystyle a\) paraméterről tudjuk, hogy \(\displaystyle 1\le{a}\le{\root 3\of {5}}\). Rögzítsük az \(\displaystyle a\) paramétert és tekintsük az \(\displaystyle f(s)=s^{2}+(a-3)s+a-4,\) az \(\displaystyle s\) változóra nézve másodfokú függvényt, ahol \(\displaystyle 0\le{s}\le{3},\) továbbá \(\displaystyle 1\le{a}\le{\root 3\of {5}}\approx1,71.\) (A megoldás végén az \(\displaystyle a\) szám az \(\displaystyle [1,\root 3\of {5}]\) intervallumon végigfutva minden olyan értéket felvehet, melyre fennáll a \(\displaystyle (\ast)\) feltétel.)
Indirekt feltevésünk szerint \(\displaystyle f>0,\) ezért az \(\displaystyle f=0\) másodfokú paraméteres egyenlet \(\displaystyle D\) diszkriminánsára teljesülnie kell, hogy \(\displaystyle D<0.\) Ezzel szemben: \(\displaystyle D=(a-3)^{2}-4(a-4)=a^{2}-10a+25=(a-5)^{2}>0\), ami azt jelenti, hogy az \(\displaystyle f=0\) egyenletnek mindig van valós megoldása, s ez ellentmond az indirekt feltevésnek. Ezzel beláttuk, hogy a \(\displaystyle Q<0\) indirekt állítás hamis volt, s ebből következik, hogy a \(\displaystyle Q\ge0\) egyenlőtlenség igaz. Utóbbival ekvivalens, hogy \(\displaystyle T\ge0,\) amit bizonyítani kellett.

Megjegyzések:

Ha a \(\displaystyle {\bf (**)}\) és \(\displaystyle {\bf (***)}\) egyenleteket felírjuk úgy, hogy \(\displaystyle x,y,v,z\) helyére a \(\displaystyle d,b,c,a\) számok alkotta, megfelelő kifejezések kerülnek, akkor – a beszorzások és egyszerűsítések után – rendre megkapjuk a kiindulási \(\displaystyle {\bf (*)}\) feltételt. (Ellenőrzés.)

Van-e valakinek eltérő, középiskolás levezetése? Főleg a 3. eset nem indirekt megoldása érdekelne (ha létezik ilyen egyáltalán).

Sajnos kimaradt az \(\displaystyle ab+cd=0\) lehetőség előzetes vizsgálata. Ezt most pótlom.

A 4. rész első, keretes szövege alatti két sort töröljük, helyére szúrjuk be az alábbi kiegészítést:

Köszönöm, ez megnyugtató.

A következőkben kiegészítem a II. feladatra adott bizonyításomat, s ezzel reflektálok a [838]-as hozzászólás egyik mondatára is.

Az a*b+c*d<=2 egyenlőtlenségben az egyenlőség akkor és csak akkor teljesül, ha a=b=c=d=1. 825-ös hozzászólásom folytatása. A koordináta-rendszerben ábrázolt szimmetrikus tartománynak (nem csak néhány pontot számoltam ki, de a múltkor erre nem reagáltam) és az x+y=2 egyenletű egyenesnek pontosan 1 közös pontja van. x=y=1 (a*b=x, c*d=y) a*b=1, c*d=1 Az a(3)+b(3)+c(3)+d(3)+a*b*c*d=5 a(3)+b(3)+c(3)+d(3)=4-re egyszerűsödik. Visszahelyettesítve korábbi egyenlőtlenségekbe a(3)+b(3)>=2, c(3)+d(3)>=2. Ezekből az jön, hogy a(3)+b(3)=c(3)+d(3)=2. Figyelembe véve, hogy a*b=c*d=1, készen vagyunk.

Első mondatok. Az egyenlőséget néztem.

Ott kezdem, hogy nemnegatív számokról írtál, de én végig csak pozitívakkal foglalkoztam. (Ez amúgy nem jellemző rám.) Ha a számok között a 0 is lehet, akkor máskor is megvalósul egyenlőség. Pl. a=0, b=c=d=köbgyök(5/3).

a+b+c+d<=4 állítást én írtam. Ez igaz. Belátható ez is a Lagrange-féle multiplikátor módszerrel, ami nem középiskolás út, sajnos. Most csak annyit tudok írni, hogyha felhasználjuk, hogy a*b+c*d<=2, akkor talán könnyebb belátni középiskolás módszerekkel.Talán.Gondolom ilyenkor ez is igaz: a*d+c*b<=2.

(a+c)*(b+d)=a*b+a*d+c*b+c*d

Hátha lehet ezekből valamit kihozni.

Tudna-e segíteni valaki az alábbi két kérdésben?

1) Igaz-e, amit a 4. rész utolsó előtti sorában leírtam: "Az egyenlőtlenségben egyenlőség pontosan …"? (Ma már kétségeim vannak e két mondat helyességét illetően … .)

2) A [823]-as hozzászólás végén olvasható: "Azt is megfigyeltem, hogy az \(\displaystyle a, b, c, d \) számok összege nem lehet 4-nél több."

Ez, ebben a megfogalmazásban, sejtésnek tűnik. Be tudná valaki bizonyítani, hogy \(\displaystyle a+b+c+d\le4\) ?

Végül a 4. rész:

A 3. rész: