Fórum: nem euklideszi geometria

Több mint 12 hónap eltelte után megint foglalkozni kezdtem a paralelogrammás feladattal. A megoldások itt vannak a 99-101 sorszám alatt, amelyek a számomra per pillanat kissé misztikusnak tűnnek, főleg a gyökös emeletes tört jellege miatt. Viszont az emeletes törtek sokszor a kezelhetőség rovására igen gyakran elő jönnek a nem euklideszi geometriák trigonometriájában, de egy-két jól megválasztott áthidaló megoldással révbe érkezhetünk. Azt tudjuk, hogy a koszinusztételek és a szinusztétel teljes bevetése egy megoldhatatlannak tűnő egyenletrendszerhez vezeti a feladat megoldóját. A másik út amit marcius8 is követett egy kis transzformációval eljutni <φ, ψ, ω>-hoz és innen egy pár tétel alkalmazásával a megoldáshoz is. Kaphatnánk-e egy kis segítséget, hogy milyen tételeket alkalmazhatunk vagy, ha ez nem lehetséges, akkor milyen mennyiségeket takarnak az ismétlődő gyökös mennyiségek?

Aki az előző két hozzászólásomban felírt térfogatképleteket lényegesen egyszerűbb alakban, vagy könnyebben számolhatóbb formában fel tudja írni, annak nagyon szépen megköszönöm.

A térfogatszámítás során nagyon fontos az elemi tetraéder térfogatának ismerete. Ugyanis egy poliéder mindig feldarabolható tetraéderekre, és minden tetraéder feldarabolható elemi tetraéderekre, tehát egy poliéder mindig feldarabolható elemi tetraéderekre, ekkor a poliéder térfogata egyenlő az így keletkezett elemi tetraéderek térfogatának összegével.

Elemi tetraédernek nevezzük az olyan tetraédert, amelynek van két egymásra merőleges kitérő helyzetű éle, és van egy olyan éle, amely ezt a két kitérő helyzetű egymásra merőleges élt köti össze, és merőleges erre a két élre. Ekkor ennek a tetraédernek minden lapja derékszögű háromszög.

Adott a \(\displaystyle \lambda\) paraméterű elliptikus térben egy elemi tetraéder.

Legyen ennek az elemi tetraédernek három páronként egymásra merőleges éle \(\displaystyle u_1\), \(\displaystyle u_2\), \(\displaystyle v\), amelyekre teljesül, hogy a \(\displaystyle v\) egyik végpontjából az \(\displaystyle u_1\) él indul ki, a \(\displaystyle v\) él másik végpontjából az \(\displaystyle u_2\) él indul ki.

Ekkor a tetraéder \(\displaystyle v\) élére illeszkedő oldallapsíkok merőlegesek egymásra. Ekkor a tetraéder \(\displaystyle u_1\) és \(\displaystyle u_2\) éle egymáshoz viszonyítva kitérő helyzetű és egymásra merőleges.

Ekkor a tetraéder \(\displaystyle u_1\) élére illeszkedő oldallapsíkok nem merőlegesek egymásra. Ekkor a tetraéder \(\displaystyle u_2\) élére illeszkedő oldallapsíkok nem merőlegesek egymásra.

Legyen \(\displaystyle \omega_1\) az \(\displaystyle u_1\) élre illeszkedő oldallapok hajlásszöge. Legyen \(\displaystyle \omega_2\) az \(\displaystyle u_2\) élre illeszkedő oldallapok hajlásszöge.

Legyen \(\displaystyle w\) ennek az elemi tetraédernek az az éle, amelyik a tetraéder \(\displaystyle u_1\), \(\displaystyle u_2\) éleinek azon végpontjait köti össze, amelyeket nem tartalmazza a tetraéder \(\displaystyle v\) éle. Ekkor a tetraéder \(\displaystyle v\) és \(\displaystyle w\) éle egymáshoz képest kitérő helyzetűek. Ennek a tetraédernek a \(\displaystyle w\) élére illeszkedő oldallapsíkok nem mindig merőlegesek egymásra, legyen ezeknek az oldallapsíkoknak a hajlásszöge \(\displaystyle \psi\).

Legyen \(\displaystyle \delta\) az a mennyiség, amelyre teljesül a következő összefüggés:

\(\displaystyle \tg(\frac{\delta}{\lambda})=\frac{\tg(\frac{u_1}{\lambda})*\tg(\frac{u_2}{\lambda})}{\sin(\frac{v}{\lambda})}\)

Továbbá ekkor teljesül a következő összefüggés is:

\(\displaystyle \cos(\frac{w}{\lambda})=\cos(\frac{u_1}{\lambda})\cos(\frac{u_2}{\lambda})\cos(\frac{v}{\lambda})\)

Ennek a tetraédernek a \(\displaystyle V\) térfogatát a következő képlettel lehet kiszámolni:

\(\displaystyle V=-\frac{\lambda^3}{2}\int_{x=0}^{x=\arctan\bigg(\frac{\sin\frac{v}{\lambda}}{\tg\frac{u_1}{\lambda}}\bigg)} \rm{arc tg}\big(tg\frac{\delta}{\lambda}* \tg(x)\big)dx-\frac{\lambda^3}{2}\int_{x=0}^{x=\arctan\bigg(\frac{\sin\frac{v}{\lambda}}{\tg\frac{u_2}{\lambda}}\bigg)} \rm{arc tg}\big(tg\frac{\delta}{\lambda}* \tg(x)\big)dx+\frac{\lambda^3}{2}\int_{x=0}^{x=\arctan\bigg(\frac{\tg\frac{w}{\lambda}}{\tg\frac{\delta}{\lambda}}\bigg)} \rm{arc tg}\big(tg\frac{\delta}{\lambda}* \tg(x)\big)dx \)

A térfogatszámítás során nagyon fontos az elemi tetraéder térfogatának ismerete. Ugyanis egy poliéder mindig feldarabolható tetraéderekre, és minden tetraéder feldarabolható elemi tetraéderekre, tehát egy poliéder mindig feldarabolható elemi tetraéderekre, ekkor a poliéder térfogata egyenlő az így keletkezett elemi tetraéderek térfogatának összegével.

Elemi tetraédernek nevezzük az olyan tetraédert, amelynek van két egymásra merőleges kitérő helyzetű éle, és van egy olyan éle, amely ezt a két kitérő helyzetű egymásra merőleges élt köti össze, és merőleges erre a két élre. Ekkor ennek a tetraédernek minden lapja derékszögű háromszög.

Adott a \(\displaystyle \lambda\) paraméterű hiperbolikus térben egy elemi tetraéder.

Legyen ennek az elemi tetraédernek három páronként egymásra merőleges éle \(\displaystyle u_1\), \(\displaystyle u_2\), \(\displaystyle v\), amelyekre teljesül, hogy a \(\displaystyle v\) egyik végpontjából az \(\displaystyle u_1\) él indul ki, a \(\displaystyle v\) él másik végpontjából az \(\displaystyle u_2\) él indul ki.

Ekkor a tetraéder \(\displaystyle v\) élére illeszkedő oldallapsíkok merőlegesek egymásra. Ekkor a tetraéder \(\displaystyle u_1\) és \(\displaystyle u_2\) éle egymáshoz viszonyítva kitérő helyzetű és egymásra merőleges.

Ekkor a tetraéder \(\displaystyle u_1\) élére illeszkedő oldallapsíkok nem merőlegesek egymásra. Ekkor a tetraéder \(\displaystyle u_2\) élére illeszkedő oldallapsíkok nem merőlegesek egymásra.

Legyen \(\displaystyle \omega_1\) az \(\displaystyle u_1\) élre illeszkedő oldallapok hajlásszöge. Legyen \(\displaystyle \omega_2\) az \(\displaystyle u_2\) élre illeszkedő oldallapok hajlásszöge.

Legyen \(\displaystyle w\) ennek az elemi tetraédernek az az éle, amelyik a tetraéder \(\displaystyle u_1\), \(\displaystyle u_2\) éleinek azon végpontjait köti össze, amelyeket nem tartalmazza a tetraéder \(\displaystyle v\) éle. Ekkor a tetraéder \(\displaystyle v\) és \(\displaystyle w\) éle egymáshoz képest kitérő helyzetűek. Ennek a tetraédernek a \(\displaystyle w\) élére illeszkedő oldallapsíkok nem merőlegesek egymásra, legyen ezeknek az oldallapsíkoknak a hajlásszöge \(\displaystyle \psi\).

Legyen \(\displaystyle \delta\) az a mennyiség, amelyre teljesül a következő összefüggés:

\(\displaystyle \th(\frac{\delta}{\lambda})=\frac{\th(\frac{u_1}{\lambda})*\th(\frac{u_2}{\lambda})}{\sh(\frac{v}{\lambda})}\)

Továbbá ekkor teljesül a következő összefüggés is:

\(\displaystyle \ch(\frac{w}{\lambda})=\ch(\frac{u_1}{\lambda})\ch(\frac{u_2}{\lambda})\ch(\frac{v}{\lambda})\)

Ennek a tetraédernek a \(\displaystyle V\) térfogatát a következő képlettel lehet kiszámolni:

\(\displaystyle V=+\frac{\lambda^3}{2}\int_{x=0}^{x=\arctan\bigg(\frac{\sh\frac{v}{\lambda}}{\th\frac{u_1}{\lambda}}\bigg)} \rm{arc th}\big(th\frac{\delta}{\lambda}* \tg(x)\big)dx+\frac{\lambda^3}{2}\int_{x=0}^{x=\arctan\bigg(\frac{\sh\frac{v}{\lambda}}{\th\frac{u_2}{\lambda}}\bigg)} \rm{arc th}\big(th\frac{\delta}{\lambda}* \tg(x)\big)dx-\frac{\lambda^3}{2}\int_{x=0}^{x=\arctan\bigg(\frac{\th\frac{w}{\lambda}}{\th\frac{\delta}{\lambda}}\bigg)} \rm{arc th}\big(th\frac{\delta}{\lambda}* \tg(x)\big)dx \)

Legyenek egy húrnégyszög oldalai ebben a sorrendben a \(\displaystyle \lambda\) paraméterű hiperbolikus síkon: \(\displaystyle a\), \(\displaystyle b\), \(\displaystyle c\), \(\displaystyle d\). A húrnégyszög \(\displaystyle e\) átlója az \(\displaystyle a\) és \(\displaystyle b\) oldalak közös végpontját és a \(\displaystyle c\) és \(\displaystyle d\) oldalak közös végpontját köti össze. A húrnégyszög \(\displaystyle f\) átlója az \(\displaystyle b\) és \(\displaystyle c\) oldalak közös végpontját és a \(\displaystyle d\) és \(\displaystyle a\) oldalak közös végpontját köti össze.

Ekkor a következő összefüggések teljesülnek:

\(\displaystyle \sh(\frac{e}{2\lambda})=\sqrt{\frac{\big(\sh(\frac{a}{2\lambda})\sh(\frac{c}{2\lambda})+\sh(\frac{b}{2\lambda})\sh(\frac{d}{2\lambda})\big)\big(\sh(\frac{a}{2\lambda})\sh(\frac{b}{2\lambda})+\sh(\frac{c}{2\lambda})\sh(\frac{d}{2\lambda})\big)}{\big(\sh(\frac{a}{2\lambda})\sh(\frac{d}{2\lambda})+\sh(\frac{b}{2\lambda})\sh(\frac{c}{2\lambda})\big)}}\)

\(\displaystyle \sh(\frac{f}{2\lambda})=\sqrt{\frac{\big(\sh(\frac{a}{2\lambda})\sh(\frac{c}{2\lambda})+\sh(\frac{b}{2\lambda})\sh(\frac{d}{2\lambda})\big)\big(\sh(\frac{a}{2\lambda})\sh(\frac{d}{2\lambda})+\sh(\frac{b}{2\lambda})\sh(\frac{c}{2\lambda})\big)}{\big(\sh(\frac{a}{2\lambda})\sh(\frac{b}{2\lambda})+\sh(\frac{c}{2\lambda})\sh(\frac{d}{2\lambda})\big)}}\)

Ezt a két összefüggést összeszorozva adódik a Ptolemaiosz-tétel:

\(\displaystyle \sh(\frac{e}{2\lambda})\sh(\frac{f}{2\lambda})=\sh(\frac{a}{2\lambda})\sh(\frac{c}{2\lambda})+\sh(\frac{b}{2\lambda})\sh(\frac{d}{2\lambda})\)

Legyen \(\displaystyle R\) a húrnégyszög köré írt kör sugara.

\(\displaystyle \sh(\frac{R}{\lambda})=\sqrt{\frac{4\big(\sh(\frac{a}{2\lambda})\sh(\frac{b}{2\lambda})+\sh(\frac{c}{2\lambda})\sh(\frac{d}{2\lambda})\big)\big(\sh(\frac{a}{2\lambda})\sh(\frac{c}{2\lambda})+\sh(\frac{b}{2\lambda})\sh(\frac{d}{2\lambda})\big)\big(\sh(\frac{a}{2\lambda})\sh(\frac{d}{2\lambda})+\sh(\frac{b}{2\lambda})\sh(\frac{c}{2\lambda})\big)}{\big(-\sh(\frac{a}{2\lambda})+\sh(\frac{b}{2\lambda})+\sh(\frac{c}{2\lambda})+\sh(\frac{d}{2\lambda})\big)\big(+\sh(\frac{a}{2\lambda})-\sh(\frac{b}{2\lambda})+\sh(\frac{c}{2\lambda})+\sh(\frac{d}{2\lambda})\big)\big(+\sh(\frac{a}{2\lambda})+\sh(\frac{b}{2\lambda})-\sh(\frac{c}{2\lambda})+\sh(\frac{d}{2\lambda})\big)\big(+\sh(\frac{a}{2\lambda})+\sh(\frac{b}{2\lambda})+\sh(\frac{c}{2\lambda})-\sh(\frac{d}{2\lambda})\big) }}\)

Legyen \(\displaystyle s\) a húrnégyszög kerületének fele, és legyen \(\displaystyle T\) a húrnégyszög területe.

\(\displaystyle \tg(\frac{T}{4\lambda^2})=\sqrt{\frac{\sh(\frac{s-a}{2\lambda})\sh(\frac{s-b}{2\lambda})\sh(\frac{s-c}{2\lambda})\sh(\frac{s-d}{2\lambda})}{\ch(\frac{s-a}{2\lambda})\ch(\frac{s-b}{2\lambda})\ch(\frac{s-c}{2\lambda})\ch(\frac{s-d}{2\lambda})-\sh(\frac{s-a}{2\lambda})\sh(\frac{s-b}{2\lambda})\sh(\frac{s-c}{2\lambda})\sh(\frac{s-d}{2\lambda})}}\)

Javítom az előbbi (#100) hozzászólásomat!!!!

Legyen a paralelogramma a \(\displaystyle \lambda\) paraméterű elliptikus síkon. Legyen a paralelogramma átlóinak kisebb hajlásszöge 90°-\(\displaystyle \omega\), és legyen a paralelogramma átlóinak nagyobb hajlásszöge 90°+\(\displaystyle \omega\).

Legyen a paralelogramma két szemközti szögének nagysága \(\displaystyle \gamma_1=\varphi-\psi\), és legyen a paralelogramma másik két szemközti szögének nagysága \(\displaystyle \gamma_2=\varphi+\psi\), ahol \(\displaystyle \gamma_1\le\gamma_2\), és \(\displaystyle 0\le\psi\le\varphi\) egyenlőtlenségek teljesülnek. Ekkor teljesülnek a \(\displaystyle \varphi=\frac{\gamma_2+\gamma_1}{2}\) és a \(\displaystyle \psi=\frac{\gamma_2-\gamma_1}{2}\) összefüggések is. Mivel elliptikus síkon van a paralelogramma, ezért \(\displaystyle \gamma_1+\gamma_2>\pi\) egyenlőtlenség teljesül.

Legyenek a paralelogramma oldalai \(\displaystyle a\), illetve \(\displaystyle b\), ahol \(\displaystyle a\) nem nagyobb, mint \(\displaystyle b\). Ekkor a paralelogramma \(\displaystyle a\) és \(\displaystyle b\) oldalai a következőképpen számolhatóak ki:

\(\displaystyle \cos(\frac{a}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}+2}{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)      \(\displaystyle \cos(\frac{b}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}-2}{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)

Megjegyzés: A paralelogramma \(\displaystyle T\) területe a következő képlettel számítható ki:

\(\displaystyle T=\lambda^2((2\gamma_1+2\gamma_2)-2\pi)=\lambda^2(4\varphi-2\pi)\Rightarrow\varphi=\frac{\pi}{2}+\frac{T}{4\lambda^2}\)

Ezt felhasználva, a paralelogramma \(\displaystyle a\) és \(\displaystyle b\) oldalai a következőképpen számolhatók ki:

\(\displaystyle \cos(\frac{a}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}+2}{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)      \(\displaystyle \cos(\frac{b}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}-2}{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)

Érdekes feladat megszerkeszteni ezt a paralelogrammát az \(\displaystyle \omega\), \(\displaystyle \gamma_1\), \(\displaystyle \gamma_2\) szögek ismeretében.

Legyen a paralelogramma a \(\displaystyle \lambda\) paraméterű elliptikus síkon. Legyen a paralelogramma átlóinak kisebb hajlásszöge 90°-\(\displaystyle \omega\), és legyen a paralelogramma átlóinak nagyobb hajlásszöge 90°+\(\displaystyle \omega\).

Legyen a paralelogramma két szemközti szögének nagysága \(\displaystyle \gamma_1=\varphi-\psi\), és legyen a paralelogramma másik két szemközti szögének nagysága \(\displaystyle \gamma_2=\varphi+\psi\), ahol \(\displaystyle \gamma_1\le\gamma_2\), és \(\displaystyle 0\le\psi\le\varphi\) egyenlőtlenségek teljesülnek. Ekkor teljesülnek a \(\displaystyle \varphi=\frac{\gamma_2+\gamma_1}{2}\) és a \(\displaystyle \psi=\frac{\gamma_2-\gamma_1}{2}\) összefüggések is. Mivel elliptikus síkon van a paralelogramma, ezért \(\displaystyle \gamma_1+\gamma_2>\pi\) egyenlőtlenség teljesül.

Legyenek a paralelogramma oldalai \(\displaystyle a\), illetve \(\displaystyle b\), ahol \(\displaystyle a\) nem nagyobb, mint \(\displaystyle b\). Ekkor a paralelogramma \(\displaystyle a\) és \(\displaystyle b\) oldalai a következőképpen számolhatóak ki:

\(\displaystyle \cos(\frac{a}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}+2}{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)      \(\displaystyle \cos(\frac{b}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}-2}{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)

Megjegyzés: A paralelogramma \(\displaystyle T\) területe a következő képlettel számítható ki:

\(\displaystyle T=\lambda^2((2\gamma_1+2\gamma_2)-2\pi)=\lambda^2(4\varphi-2\pi)\Rightarrow\varphi=\frac{\pi}{2}+\frac{T}{4\lambda^2}\)

Ezt felhasználva, a paralelogramma \(\displaystyle a\) és \(\displaystyle b\) oldalai a következőképpen számolhatók ki:

\(\displaystyle \ch(\frac{a}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}+2}{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)      \(\displaystyle \ch(\frac{b}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}-2}{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)

Érdekes feladat megszerkeszteni ezt a paralelogrammát az \(\displaystyle \omega\), \(\displaystyle \gamma_1\), \(\displaystyle \gamma_2\) szögek ismeretében.

Legyen a paralelogramma a \(\displaystyle \lambda\) paraméterű hiperbolikus síkon. Legyen a paralelogramma átlóinak kisebb hajlásszöge 90°-\(\displaystyle \omega\), és legyen a paralelogramma átlóinak nagyobb hajlásszöge 90°+\(\displaystyle \omega\).

Legyen a paralelogramma két szemközti szögének nagysága \(\displaystyle \gamma_1=\varphi-\psi\), és legyen a paralelogramma másik két szemközti szögének nagysága \(\displaystyle \gamma_2=\varphi+\psi\), ahol \(\displaystyle \gamma_1\le\gamma_2\), és \(\displaystyle 0\le\psi\le\varphi\) egyenlőtlenségek teljesülnek. Ekkor teljesülnek a \(\displaystyle \varphi=\frac{\gamma_2+\gamma_1}{2}\) és a \(\displaystyle \psi=\frac{\gamma_2-\gamma_1}{2}\) összefüggések is. Mivel hiperbolikus síkon van a paralelogramma, ezért \(\displaystyle \gamma_1+\gamma_2<\pi\) egyenlőtlenség teljesül.

Legyenek a paralelogramma oldalai \(\displaystyle a\), illetve \(\displaystyle b\), ahol \(\displaystyle a\) nem nagyobb, mint \(\displaystyle b\). Ekkor a paralelogramma \(\displaystyle a\) és \(\displaystyle b\) oldalai a következőképpen számolhatóak ki:

\(\displaystyle \ch(\frac{a}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}-2}{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)      \(\displaystyle \ch(\frac{b}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}+2}{\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\varphi)}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)

Megjegyzés: A paralelogramma \(\displaystyle T\) területe a következő képlettel számítható ki:

\(\displaystyle T=\lambda^2(2\pi-(2\gamma_1+2\gamma_2))=\lambda^2(2\pi-4\varphi)\Rightarrow\varphi=\frac{\pi}{2}-\frac{T}{4\lambda^2}\)

Ezt felhasználva, a paralelogramma \(\displaystyle a\) és \(\displaystyle b\) oldalai a következőképpen számolhatók ki:

\(\displaystyle \ch(\frac{a}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}-2}{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)      \(\displaystyle \ch(\frac{b}{\lambda})=\frac{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}+\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}+2}{\sqrt{\frac{\ctg^2(\omega)}{\sin^2(\frac{T}{4\lambda^2})}+1}-\sqrt{\frac{\ctg^2(\omega)}{\cos^2(\psi)}+1}}\)

Érdekes feladat megszerkeszteni ezt a paralelogrammát az \(\displaystyle \omega\), \(\displaystyle \gamma_1\), \(\displaystyle \gamma_2\) szögek ismeretében.

Nagyon szépen köszönöm gyula60, hogy érdemben foglalkoztál a problémával!!!!!

Igen, ezt a képletet más alakban ismerem. Csak úgy vezetem le, hogy először az "x/2", "y/2", "a" oldalú háromszög "a" oldalára írom fel a koszinusztételt, másodszor az "x/2", "y/2", "b" oldalú háromszög "b" oldalára írom fel a koszinusztételt, végül ezt a két koszinusztételt összeadom. Közben felhasználom, hogy a felírt koszinusztételekben az "x/2" és az "y/2" oldalak által bezárt szögek összege 180°, így ezeknek a szögeknek a koszinuszai egymás ellentettjei. Ez az összefüggés megfelel annak az euklideszi síkon érvényes összefüggésnek, hogy a paralelogramma oldalainak négyzetösszege egyenlő az átlóinak négyzetösszegével. De ezzel együtt is még egy kezelhetetlen egyenlettel találkoztam. Tisztelettel: marcius8.

Rugalmas anyagból lehetséges gömbi, illetve hiperbolikus szövetet létrehozni. Gömbi szövet például egy sapka, hiperbolikus szövetet egyelőre nem nagyon árulnak, korallhoz hasonló sálat lehet venni, meg mondjuk ágytakaró készítéséhez itt egy tutorial: geometrygames.org/HyperbolicBlanket/

Kérdésem: van-e annak értelme, hogy 3 dimenziós hiperbolikus anyagot hozzunk létre? Ha nem is fér el, el tudunk-e képzelni valamit, amire azt mondhatjuk, hogy na ez egy hiperbolikus tömb. Nagyon puha és képlékeny anyagból. Például milyen jelenséget produkálna, várnánk el tőle?

A hiperbolikus síkon sokat segíthet a következő összefüggés:

\(\displaystyle (ch(a)+ch(b))^2 = (ch(x)+1)(ch(y)+1)\)

Ahol a és b a szóban forgó paralelogramma szomszédos oldalai és x, y a megfelelő átlók és ch(x) a koszinusz hiperbolikusz függvény. Az oldalak hajlásszöge az átlók mentén még felbontható két parciálisra. Ezek egyikére kétféleképpen is felírható az oldalakra vonatkozó koszinusztétel. Így nyerhető a fenti összefüggés.

Cayley-Klein modellben legyen \(\displaystyle k\) az abszolút kúpszelet (a modell határköre). Tekintsünk egy tetszőleges \(\displaystyle ABC\) háromszöget, legyen \(\displaystyle P\) tetszőleges további pont. A vizsgált Ceva-tulajdonságú egyenesek ekkor \(\displaystyle PA\), \(\displaystyle PB\), \(\displaystyle PC\). Legyenek a \(\displaystyle BC\), \(\displaystyle CA\), \(\displaystyle AB\) oldalegyenesek \(\displaystyle k\)-ra vonatkozó pólusai rendre \(\displaystyle A_1\), \(\displaystyle B_1\), \(\displaystyle C_1\); valamint a \(\displaystyle PA\), \(\displaystyle PB\), \(\displaystyle PC\) egyenesek \(\displaystyle k\)-ra vonatkozó pólusai rendre \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\).

Ekkor az új háromszög oldalai tetszőleges \(\displaystyle A_2\), \(\displaystyle B_2\), \(\displaystyle C_2\)-n áthaladó egyenesek. Legyen ez az új háromszög \(\displaystyle A'B'C'\), úgy, hogy \(\displaystyle C_2\in A'B'\), \(\displaystyle B_2\in A'C'\), \(\displaystyle C_2\in A'B'\). Azt kell belátnunk, hogy ekkor \(\displaystyle A'A_1\), \(\displaystyle B'B_1\), \(\displaystyle C'C_1\) konkurrens egyenesek.

A bizonyítandó ekvivalens azzal, hogy az \(\displaystyle A'B'C'\) és \(\displaystyle A_1B_1C_1\) háromszögek pontra nézve perspektívek, így a Desargues-tétel megfordítása miatt elég azt belátnunk, hogy tengelyre nézve perspektívek.

Ehhez vizsgáljuk először az \(\displaystyle A'B'\cap A_1B_1\) metszéspontot. Ennek a polárisát keressük meg.
- \(\displaystyle A_1B_1\) pólusa \(\displaystyle C\).
- Mivel \(\displaystyle A'B'\) tartalmazza \(\displaystyle C_2\), \(\displaystyle A'B'\) pólusa rajta van \(\displaystyle C_2\) polárisán, azaz \(\displaystyle PC\)-n.
Ez azt jelenti, hogy \(\displaystyle A_1B_1\) pólusát \(\displaystyle A'B'\) pólusával összekötő egyenes (tehát \(\displaystyle A'B'\cap A_1B_1\) polárisa) éppen \(\displaystyle PC\).

Hasonlóan látható, hogy \(\displaystyle B'C'\cap B_1C_1\) polárisa \(\displaystyle PA\) és \(\displaystyle A'C'\cap A_1C_1\) polárisa \(\displaystyle PB\). Mivel ezek konkurrensek, a vizsgált metszésponok (a konkurrens polárisok pólusai) kollineárisak. Tehát \(\displaystyle A'B'C'\) és \(\displaystyle A_1B_1C_1\) tengelyre nézve perspektívek, és ezt kellett belátnunk.

Euklideszi síkon ha adottak az a,b,c, és a',b',c' irányok, akkor ezek egyszerre Ceva-tulajdonságúak egymásra nézve.

Értve ez alatt azt, hogy egy a,b,c irányú oldalakkal rendelkező ABC háromszög csúcsaiba állítva a',b',c' irányú egyeneseket ezek egy ponton mennek át pontosan akkor, ha ez az a',b',c' oldalirányú A'B'C' háromszögre is teljesül.

Ez az állítás hiperbolikus síkon ahogy nézem nem igaz, vagy nem sikerült jól lefordítanom.

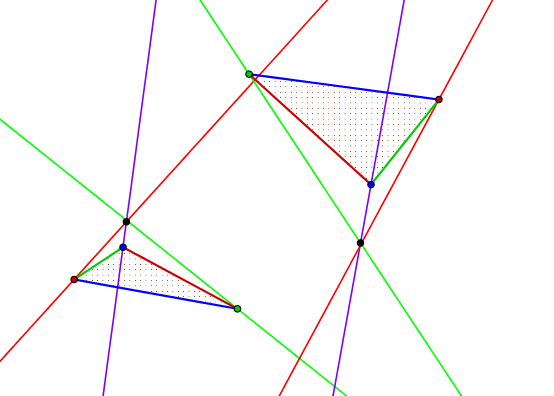
Igaz viszont az, hogy ha ABC háromszöghöz a',b',c' egyenesek Cevák, akkor egy, a',b',c' egyenesekre merőleges oldalú háromszöghöz az a,b,c egyenesekre merőleges egyenesek Cevák. (Euklideszi esetben ez az A'B'C' háromszög és a csúcsaiba állított egyenesek 90 fokos elforgatását jelentené, ez egybevágóság, speciálisan az egy ponton átmenést megtartja, lásd ábra.)

Bizonyítsd be az állítást.

(ha a metszéspont nem jön létre, akkor a három egyenes párhuzamos vagy közös merőlegessel rendelkezik)

Nem-euklideszi geometria: Paralelogramma olyan négyszög, amelyre a következő tulajdonságok teljesülnek: 1. Középpontosan szimmetrikus. 2. Szemközti oldalak egyforma hosszúak. 3. Szemközti szögek egyforma nagyságúak. 4. Átlók felezik egymást.

Az euklideszi geometriában a paralelogrammának két további tulajdonsága is van: 5. Szemközti oldalak párhuzamosak. 6. Szomszédos szögek összege 180°. Ez a két tulajdonság a nem- euklideszi geometriában nem teljesülhet.

Én legalábbis ezt értem paralelogramma alatt.

Paralelogramma alatt itt középpontosan szimmetrikus négyszöget értsz, ugye?

Akkor én is mondok egy feladatot: Ismert az elliptikus vagy hiperbolikus síkon egy paralelogrammának a szögei és ismert ugyanennek a paralelogrammának az átlóinak a hajlásszöge. Mekkorák a paralelogramma oldalai?

Érdekes feladat, biztosan fogok rajta gondolkozni. Gyanítom, hogy a hiperbolikus síkon az egyenlőtlenség megfordul....

Egy gömbháromszög szögei \(\displaystyle \alpha, \beta, \gamma\), a velük szemközti oldalívek hossza \(\displaystyle a\), \(\displaystyle b\), illetve \(\displaystyle c\). Igazoljuk, hogy

\(\displaystyle a\cdot \cos\beta + b \cdot\cos\alpha < c. \)

(IMC2002/2/4; KöMaL A. 298.)

Az euklideszi síkban egyenlőség lenne.

Első "feladat":

Legyenek az \(\displaystyle S^2\) gömbön most a "pontok" az ellentétes pontpárok, a szakaszok az ellentétes szakaszpárok, egy szakasz "belső felezőpontja" a felezőpontja, a "külső felezőpontja" pedig ugyanannak a szakasz végpontjainak másik felezőpontja, amelyik nem esik rá a szakaszra (merőleges a belső felezőponttal).

BBH.: Egy tetszőleges gömbháromszög három oldalának külső felezőpontjai egy egyenesre esnek. (Ez könnyű.)

Hol van ennek az egyenesnek a "középpontja"?

BBH.: Két belső felezőpont egyenese átmegy egy külső felezőponton. (Tehát ugyanaz a konfiguráció, mint mondjuk a három kör hasonlósági pontjainál áll fenn.)

Milyen állítást kapunk a síkon, ha ezeket az állításokat levetítjük?

Milyen összefüggést kapunk, ha az ábrának vesszük a duálisát a gömbön, azaz, pontpárból merőleges főkört, főkörből merőleges pontpárt képzünk?

((Van-e ennek az állításnak analogonja \(\displaystyle S^3\)-ban tetraéderre?))

- - - - - - -

.. én nem igazán ismerek/találok jó gömbi feladatokat. Szóval szívesen veszem őket.

Talán méltatlanul van/volt hanyagolva a gömb. Az inverziók elmélete itt teljes, a három dimenziós euklideszi térben hasznos ismerni, a projektív geometria állításai is sokkal szebbek a gömb saját geometriájában, stb.

Még ha épp ezért is úgy érezzük, hogy szinte teljesen ismerjük a gömböt (a reciprocitás, proj.geo. stb eredményei révén), akármikor szembejöhet olyan feladat, amelyik véletlenül a gömbök egy "saját" tételének vetülete a síkon, ...

Az ábrán látható a szög "duplázása", vagyis a "dupla" szögnek megfelelő ív megszerkesztése.

Nyilván ez valamilyen módon additív kell legyen hogy legyen értelme a kérdésnek, ellipszisre momentán a sima szög, csak elaffinítva.

A paraboláknak is saját esetük van.

Ha a kúpszelet kör, akkor ez a szokásos szöggel egyezik meg. Ha a kúpszelet ellipszis, akkor alkalmazzunk az egész síkra egy olyan affinitást, amitől kör lesz, ez az általad definiált szöget nem változtatja meg. Ha hiperbola, akkor más a helyzet, ilyenkor ezt a szöget nem lehet visszavezetni a kör esetére, tehát két lényegesen különböző eset van. Azt nem tudom, hogy olyankor szögfelezőt hogy lehet szerkeszteni.

[S1]. Feladat (Az S engem jelöl) Érzékelik-e egy síknégyzet lakói geometriailag, ha feltekerem a világukat egy hengerré? (megváltozik-e a távolság, szög lokálisan, globálisan, az egyenesek vonalai?)

És ha rétessé tekerem fel őket, azaz, nem ugyanakkora görbülettel mindenhol?

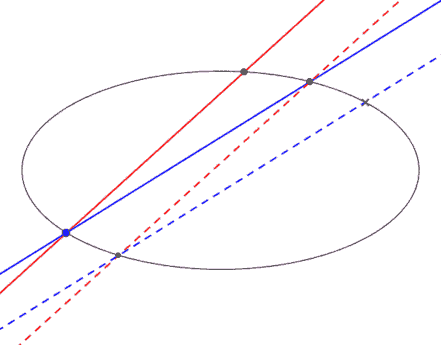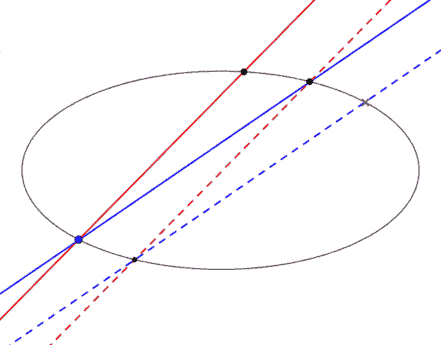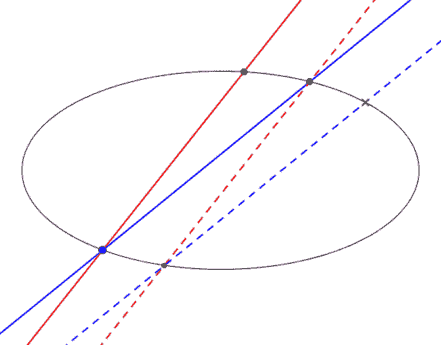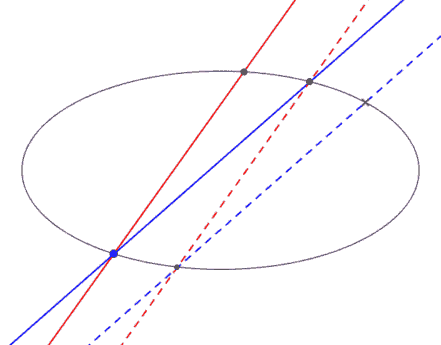
Két egyenes közti szöget definiáljuk a következőképp:

1: ha e||e' és f||f', akkor ef< = e'f'< 2: adott egy c kúpszelet, és rajta AB pontok. A kúpszelet egyik ívének minden pontjából ugyanakkora szögből látszódik AB.

(ez a két megkövetelt tulajdonság nem vezet ellentmondásra)

Kérdés: Hogyan szerkesztünk szögfelezőt minél egyszerűbben?

(ábra: ha ily módon másolok át szöget-ívet, akkor a kék pont helyzetétől függetlenül a kék szaggatott egyenes ugyanazt a pontot metszi ki c-ből)

Köszönöm az útmutatást, de a Coxeter könyvben ezek az ekvivalenciák nem szerepelnek. Tisztelettel: Bertalan Zoltán.