| [1241] BerkoErzsebet | 2025-03-13 08:07:16 |
 Mi köze van a kártyalapoknak a most lejárt trigonometrikus egyenlőtlenséghez (B. 5441.)? Ha A + B + C = pi, akkor cosA + cosB + cosC = 1 + 4*sin(A/2)sin(B/2)sin(C/2), illetve sin(A/2) + sin(B/2) + sin(C/2) = 1 + 4*sin((A+B)/4)sin((B+C)/4)sin((C+A)/4). Kell: sin((A+B)/4)sin((B+C)/4)sin((C+A)/4) >= sin(A/2)sin(B/2)sin(C/2)
A szögek összege pi/2 mindkét oldalon. Az A/2 és B/2 átlaga: (A+B)/4.
Nézzünk 3 számot: pl. 2, 4 és 6. Vegyük mindig a páronkénti átlagok szorzatát. Az összeg változatlan. A szorzat pedig tart 4*4*4=64-hez monoton növekedve.
2*4*6=48 3*5*4=60 4*4,5*3,5=63 4,25*4*3,75=63,75 ...
2 + 4 + 6 = 3 + 5 + 4 = ...
A példában persze van egy szinuszfüggvény is. Az (0; pi/2)-n monoton.
Láttam már olyan kártyás feladatot, kártyatrükköt, ahol a kártyalap is bement középre.
|
|
|
| [1239] Sinobi | 2025-03-12 22:46:16 |
 A csupa piros sor különleges a definíció szerint. (A megoldás ezzel kezd amúgy.)
Ha így nem tetszik, talán átfogalmazva jobb: "Minden kékre igaz a Feltétel" helyett "nincs olyan kék, amelyre nem igaz a Feltétel". Ez igaz a csupa piros sorra. (Akármi is legyen a feltétel.)
|
|
|
|
| [1236] Lpont | 2025-03-11 01:06:00 |
 A C.1844 feladathoz
Ha a piros főátló alatti összes mező kék, a főátló felettiek (és a főátló is) pedig pirosak, azaz a kék mezőkre i>j.
Ekkor bármely kék színű mező sorában (k-adik sor) minden piros mező a kékektől jobbra (és a főátlóban vagy a főátló felett) helyezkedik el, vagyis az l>k vagy l=k reláció teljesül.
Fentiekből l>k>j vagy l=k>j következik, azaz l>j.
Különleges csak akkor lehet ez a sor, ha (l;j) is piros, de ez a mező l>j miatt szintén a főátló alatt helyezkedik el, ahol minden mező kék színű.
Ilyen színezés elérhető, ha Laci mindig egy főátló alatti - még nem színezett -mezőt színez kékre, míg Ági a feladat feltétele miatt kénytelen annak a főátlóra vett tükörképét pirosra színezni.
Ebben az esetben Ági nem talál különleges sort, ellentétben a bizonyítandóval.
|
|
|
| [1234] marcius8 | 2025-02-23 16:00:40 |
 Az előző hozzászólásom végét javítom:
\displaystyle r^2‒d_A^2=4x*(y(z‒x)+z(y‒x))/(9a)
\displaystyle r^2‒d_B^2=4y*(z(x‒y)+x(z‒y))/(9b)
\displaystyle r^2‒d_C^2=4z*(x(y‒z)+y(x‒z))/(9c)
A feltevés miatt: \displaystyle 0<a≤b≤c azaz \displaystyle x≥y≥z>0.
Ezért \displaystyle z‒x≤0 és \displaystyle y‒x≤0, így \displaystyle 4x*(y(z‒x)+z(y‒x))/(9a)≤0, így \displaystyle r≤d_A, azaz az \displaystyle A pont az \displaystyle ABC háromszögbe írt körön kívül, vagy annak határán helyezkedik el.
Ezért \displaystyle y‒z≥0 és \displaystyle x‒z≥0, így \displaystyle 4z*(x(y‒z)+y(x‒z))/(9c)≥0, így \displaystyle r≥d_C, azaz az \displaystyle C pont az \displaystyle ABC háromszögbe írt körön belül, vagy annak határán helyezkedik el.
|
 |
| Előzmény: [1233] marcius8, 2025-02-23 15:01:50 |
|
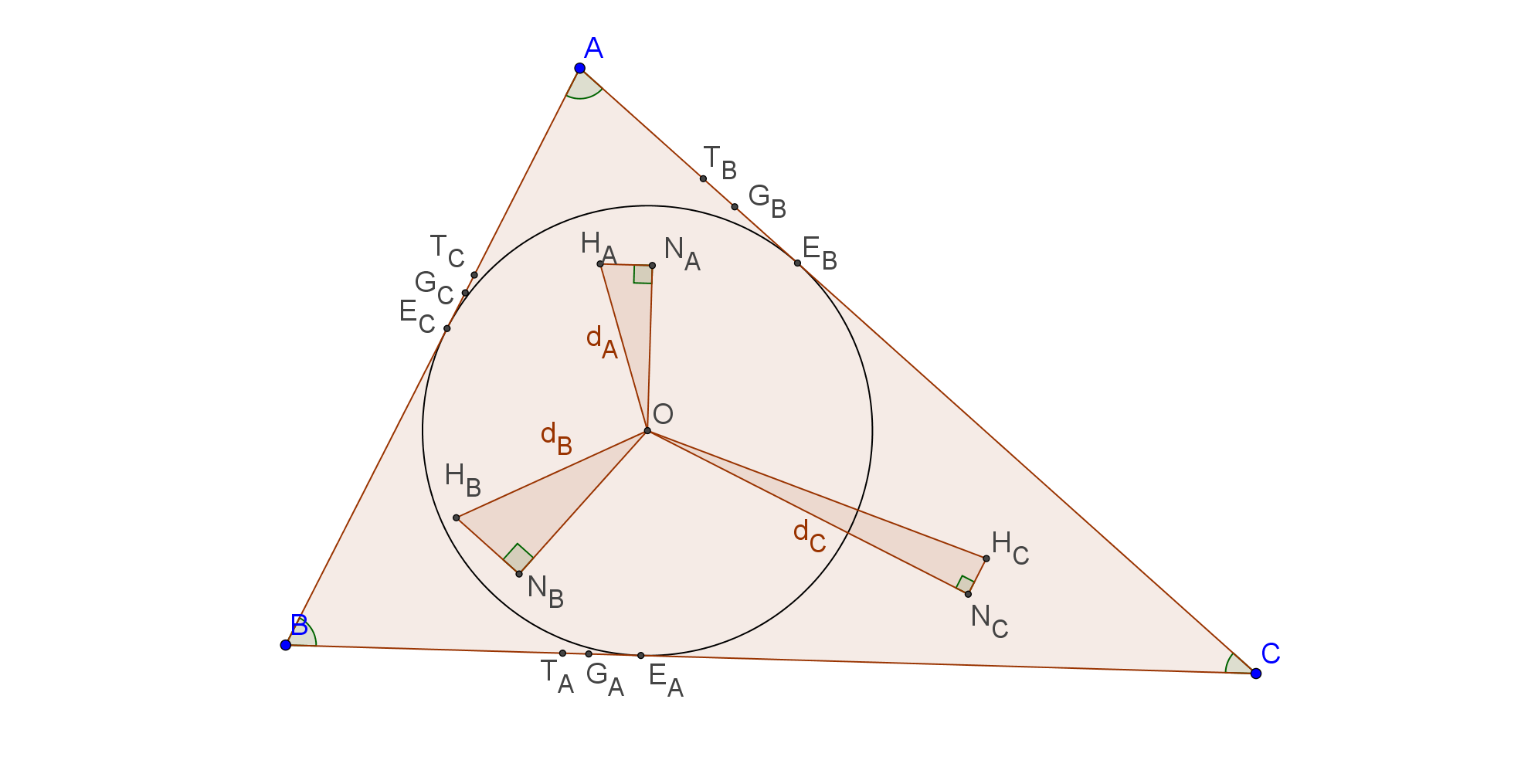
| [1233] marcius8 | 2025-02-23 15:01:50 |
 B.5435
Én a következőképpen számoltam:
Az áttekinthetőség érdekében a következőképpen fogalmazom át a feladatot:
B.5435. Az ABC háromszög beírt köre a BC=a, AC=b, AB=c oldalakat rendre az \displaystyle E_A, \displaystyle E_B, \displaystyle E_C pontokban érinti. Legyen továbbá \displaystyle H_A, \displaystyle H_B, \displaystyle H_C pontok rendre az \displaystyle AE_A, \displaystyle BE_B és \displaystyle CE_C szakaszok A-hoz, B-hez, illetve C-hez közelebbi harmadolópontja. Mutassuk meg, hogy a \displaystyle H_A, \displaystyle H_B, \displaystyle H_C pontok közül legalább egy a beírt kör belsejében vagy határán van.
A megoldáshoz felhasználom, hogy az \displaystyle a, \displaystyle b, \displaystyle c pozitív számok pontosan akkor lehetnek egy háromszög oldalai, ha vannak olyan \displaystyle x, \displaystyle y, \displaystyle z pozitív számok, melyekre teljesül, hogy \displaystyle a=y+z, \displaystyle b=x+z, \displaystyle c=x+y. Ez az állítás a háromszög-egyenlőtlenség felhasználásával könnyen igazolható. Továbbá ekkor ha \displaystyle s a háromszög kerületének fele, akkor \displaystyle x=s-a, \displaystyle y=s-b, \displaystyle z=s-c és ekkor \displaystyle s=x+y+z. Továbbá ekkor \displaystyle a≤b≤c pontosan akkor teljesül, ha \displaystyle x≥y≥z. A továbbiakban így használom az \displaystyle a=y+z, \displaystyle b=x+z, \displaystyle c=x+y helyettesítéseket, és felteszem, hogy \displaystyle 0<a≤b≤c, azaz \displaystyle x≥y≥z>0. Ekkor bebizonyítom, hogy \displaystyle H_C biztosan az \displaystyle ABC háromszögbe írt körön belül vagy annak határán helyezkedik el, \displaystyle H_A biztosan az \displaystyle ABC háromszögbe írt körön kívül vagy annak határán helyezkedik el. Az könnyen látható, hogy szabályos háromszög esetén a \displaystyle H_A, \displaystyle H_B, \displaystyle H_C pontok mindegyike az \displaystyle ABC háromszögbe írt kör kerületén van.
Legyenek α, β, γ az ABC háromszög \displaystyle a, \displaystyle b, \displaystyle c oldalaival szemközti szögei. Legyen \displaystyle t az \displaystyle ABC háromszög területe.
Legyenek \displaystyle T_A, \displaystyle T_B, \displaystyle T_C pontok az \displaystyle ABC háromszög \displaystyle A, \displaystyle B, \displaystyle C csúcsainak az \displaystyle a, \displaystyle b, \displaystyle c oldalaira eső merőleges vetületei.
Legyenek \displaystyle m_A=AT_A, \displaystyle m_B=BT_B, \displaystyle m_C=CT_C az \displaystyle ABC háromszög \displaystyle a, \displaystyle b, \displaystyle c oldalaihoz tartozó magasságai.
Legyenek \displaystyle G_A, \displaystyle G_B, \displaystyle G_C pontok a \displaystyle H_A, \displaystyle H_B, \displaystyle H_C pontoknak az \displaystyle a, \displaystyle b, \displaystyle c oldalaira eső merőleges vetületei.
Legyen \displaystyle O az \displaystyle ABC háromszögbe írt \displaystyle k kör középpontja, és legyen \displaystyle r=\sqrt{x*y*z/s} ennek a körnek a sugara.
Legyenek \displaystyle N_A, \displaystyle N_B, \displaystyle N_C pontok rendre a \displaystyle H_A, \displaystyle H_B, \displaystyle H_C pontoknak az \displaystyle E_AO, \displaystyle E_BO, \displaystyle E_CO egyenesekre eső merőleges vetületei.
Ekkor a következő számolásokat lehet elvégezni (kevésbé részletezve):
\displaystyle T_AE_A=x*|z‒y|/(z+y), innen: \displaystyle N_AH_A=G_AE_A=2*T_AE_A/3=(2x|z‒y|)/(3(z+y)).
\displaystyle T_BE_B=y*|x‒z|/(x+z), innen: \displaystyle N_BH_B=G_BE_B=2*T_BE_B/3=(2y|x‒z|)/(3(x+z)).
\displaystyle T_CE_C=z*|y‒x|/(y+x), innen: \displaystyle N_CH_C=G_CE_C=2*T_CE_C/3=(2x|y‒x|)/(3(y+x)).
\displaystyle m_A=2t/a=2*\sqrt{s*x*y*z}/a, innen: \displaystyle H_AG_A=2/3*m_A=4/3*\sqrt{s*x*y*z}/a. \displaystyle m_B=2t/b=2*\sqrt{s*x*y*z}/b, innen: \displaystyle H_BG_B=2/3*m_B=4/3*\sqrt{s*x*y*z}/b. \displaystyle m_C=2t/c=2*\sqrt{s*x*y*z}/c, innen: \displaystyle H_CG_C=2/3*m_C=4/3*\sqrt{s*x*y*z}/c.
\displaystyle ON_A=|N_AE_A‒OE_A|=|N_AE_A‒r|=|H_AG_A‒r|=((3*x+s)*t)/(3*s*a). \displaystyle ON_B=|N_BE_B‒OE_B|=|N_BE_B‒r|=|H_BG_B‒r|=((3*y+s)*t)/(3*s*b). \displaystyle ON_C=|N_CE_C‒OE_C|=|N_CE_C‒r|=|H_CG_C‒r|=((3*z+s)*t)/(3*s*c).
A \displaystyle H_A pont \displaystyle d_A=OH_A távolsága az \displaystyle O ponttól a \displaystyle H_AN_AO derékszögű háromszögből (\displaystyle ON_A, \displaystyle N_AH_A befogók, \displaystyle d_A=OH_A átfogók): \displaystyle d_A=\sqrt{ON_A^2+H_AO^2}
A \displaystyle H_B pont \displaystyle d_B=OH_B távolsága az \displaystyle O ponttól a \displaystyle H_BN_BO derékszögű háromszögből (\displaystyle ON_B, \displaystyle N_BH_B befogók, \displaystyle d_B=OH_B átfogók): \displaystyle dB=\sqrt{ON_B^2+H_BO^2}
A \displaystyle H_C pont \displaystyle d_C=OH_C távolsága az \displaystyle O ponttól a \displaystyle H_CN_CO derékszögű háromszögből (\displaystyle ON_C, \displaystyle N_CH_C befogók, \displaystyle d_C=OH_C átfogók): \displaystyle d_C=\sqrt{ON_C^2+H_CO^2}
Elvégezve a számolásokat:
\displaystyle d_A=\sqrt{x(+1ayz+4xbz+4xyc)/(9sa)}
\displaystyle d_B=\sqrt{y(+4ayz+1xbz+4xyc)/(9sb)}
\displaystyle d_C=\sqrt{z(+4ayz+4xbz+1xyc)/(9sc)}
\displaystyle r^2‒d_A^2=4x*(y(z‒x)+z(y‒x))/(9a)
\displaystyle r^2‒d_B^2=4y*(z(x‒y)+x(z‒y))/(9b)
\displaystyle r^2‒d_C^2=4z*(x(y‒z)+y(x‒z))/(9c)
A feltevés miatt: \displaystyle 0<a≤b≤c azaz \displaystyle x≥y≥z>0.
Ezért \displaystyle z‒x≤0 és \displaystyle y‒x≤0, így \displaystyle 4x*(y(z‒x)+z(y‒x))/(9a)≤0, így \displaystyle r≤d_A, azaz az \displaystyle A pont az \displaystyle ABC háromszögbe írt körön kívül, vagy annak határán helyezkedik el.
Ezért \displaystyle y‒z≥0 és \displaystyle x‒z≥0, így \displaystyle z*(x(y‒z)+y(x‒z))/(9c)≥0, így \displaystyle r≥d_C, azaz az \displaystyle C pont az \displaystyle ABC háromszögbe írt körön belül, vagy annak határán helyezkedik el.
|
|
| [1232] marcius8 | 2025-01-19 19:56:49 |
 Még mindig a B.5429 feladattal vagyok:
Segédtétel: Ha az \displaystyle M, \displaystyle M_1, \displaystyle M_2, \displaystyle K, \displaystyle L pontok közül az \displaystyle M pont rajta van az \displaystyle M_1 és \displaystyle M_2 pontok által meghatározott egyenesen, akkor a következő összefüggés teljesül: \displaystyle [MM_1K][MM_2L]=[MM_1L][MM_2K]
Segédtétel bizonyítása: Legyen \displaystyle m_1=MM_1, \displaystyle m_2=MM_2, ,legyen \displaystyle k a \displaystyle K pont távolságsa az \displaystyle M_1M_2 egyenestől, legyen \displaystyle l az \displaystyle L pont távolsága az \displaystyle M_1M_2 egyenestől.
Ekkor \displaystyle [MM_1K]=\frac{m_1k}{2}, \displaystyle [MM_2L]=\frac{m_2l}{2}, \displaystyle [MM_1L]=\frac{m_1l}{2}, \displaystyle [MM_2K]=\frac{m_2k}{2} teljesülnek.
Ezeket az összefüggéseket beírva a bizonyítandó \displaystyle [MM_1K][MM_2L]=[MM_1L][MM_2K] összefüggésbe, egyenlőség adódik.
Segédtétel (Pascal-tétel): Az \displaystyle A, \displaystyle B, \displaystyle C, \displaystyle D, \displaystyle E, \displaystyle F pontok pontosan akkor vannak egy kúpszeleten, ha az \displaystyle AC és \displaystyle BD egyenesek \displaystyle U metszéspontja, \displaystyle AF és \displaystyle ED egyenesek \displaystyle V metszéspontja, \displaystyle BF és \displaystyle EC egyenesek \displaystyle W metszéspontja egy egyenesen vannak.
A feladat állításának bizonyítása:
Az \displaystyle C, \displaystyle A, \displaystyle U, \displaystyle W, \displaystyle B pontok között az \displaystyle C, \displaystyle A, \displaystyle U pontok egy egyenesen vannak, ezért \displaystyle [CAW][CUB]=[CAB][CUW].
Az \displaystyle F, \displaystyle A, \displaystyle V, \displaystyle B, \displaystyle E pontok között az \displaystyle F, \displaystyle A, \displaystyle V pontok egy egyenesen vannak, ezért \displaystyle [FAB][FVE]=[FAE][FVB].
Az \displaystyle B, \displaystyle D, \displaystyle U, \displaystyle C, \displaystyle W pontok között az \displaystyle B, \displaystyle D, \displaystyle U pontok egy egyenesen vannak, ezért \displaystyle [BDC][BUW]=[BDW][BUC].
Az \displaystyle B, \displaystyle F, \displaystyle W, \displaystyle V, \displaystyle D pontok között az \displaystyle B, \displaystyle F, \displaystyle W pontok egy egyenesen vannak, ezért \displaystyle [BFV][BWD]=[BFD][BWV].
Az \displaystyle E, \displaystyle D, \displaystyle V, \displaystyle F, \displaystyle C pontok között az \displaystyle E, \displaystyle D, \displaystyle V pontok egy egyenesen vannak, ezért \displaystyle [EDF][EVC]=[EDC][EVF].
Az \displaystyle C, \displaystyle E, \displaystyle W, \displaystyle A, \displaystyle V pontok között az \displaystyle C, \displaystyle E, \displaystyle W pontok egy egyenesen vannak, ezért \displaystyle [CEA][CWV]=[CEV][CWA]
Az \displaystyle W, \displaystyle U, \displaystyle V, \displaystyle C, \displaystyle B pontok között az \displaystyle W, \displaystyle U, \displaystyle V pontok egy egyenesen vannak, ezért \displaystyle [WUC][WVB]=[WUB][WVC] (Pascal-tétel: \displaystyle U, \displaystyle V, \displaystyle W pontok egy egyenesen vannak.)
Összeszorozva az egyenleteket:
\displaystyle [CAW][CUB]*[FAB][FVE]*[BDC][BUW]*[BFV][BWD]*[EDF][EVC]*[CEA][CWV]*[WUC][WVB]
\displaystyle = [CAB][CUW]*[FAE][FVB]*[BDW][BUC]*[BFD][BWV]*[EDC][EVF]*[CEV][CWA]*[WUB][WVC]
Mivel a kúpszelet nem elfajuló (parabola, ellipszis, hiperbola), ezért egyik háromszög területe sem 0. Így ha az egyenlet mindkét oldalán ugyanannak a háromszögnek a területe van, akkor ezzel a területtel lehet egyszerűsíteni. Elvégezve a lehetséges egyszerűsítéseket:
\displaystyle [ABC]*[CDE]*[EFA]*[BDF]=[BCD]*[DEF]*[FAB]*[ACE]
És ez éppen a bizonyítandó állítás. Ez a bizonyítás csak nem elfajuló kúpszeletek esetén jó.
|
|
| [1230] marcius8 | 2025-01-19 16:38:58 |
 B.5429. Megpróbálom homogén koordinátákkal ezt a megoldást.
Az \displaystyle A(x_A,y_A,z_A), \displaystyle B(x_B,y_B,z_B), \displaystyle C(x_C,y_C,z_C), \displaystyle D(x_D,y_D,z_D), \displaystyle E(x_E,y_E,z_E), \displaystyle F(x_F,y_F,z_F) pontok esetén a következő determinánst értelmezem:
\displaystyle [ABCDEF]=\det\begin{pmatrix} x_A^2&y_A^2&z_A^2&x_Ay_A&x_Az_A&y_Az_A\\
x_B^2&y_B^2&z_B^2&x_By_B&x_Bz_B&y_Bz_B\\
x_C^2&y_C^2&z_C^2&x_Cy_C&x_Cz_C&y_Cz_C\\
x_D^2&y_D^2&z_D^2&x_Dy_D&x_Dz_D&y_Dz_D\\
x_E^2&y_E^2&z_E^2&x_Ey_E&x_Ez_E&y_Ez_E\\
x_F^2&y_F^2&z_F^2&x_Fy_F&x_Fz_F&y_Fz_F\\\end{pmatrix}
Az \displaystyle A(x_A,y_A,z_A), \displaystyle B(x_B,y_B,z_B), \displaystyle C(x_C,y_C,z_C), \displaystyle D(x_D,y_D,z_D), \displaystyle E(x_E,y_E,z_E), \displaystyle F(x_F,y_F,z_F) pontok pontosan akkor vannak ugyanazon a kúpszeleten, ha a \displaystyle [ABCDEF]=0 egyenlet teljesül:
Továbbá legyen \displaystyle P(x_P,y_P,z_P), \displaystyle Q(x_Q,y_Q,z_Q), \displaystyle R(x_R,y_R,z_R) pontok esetén \displaystyle [PQR] a következő kifejezés:
\displaystyle [PQR]=1/2*det\begin{pmatrix} x_P&y_P&z_P \\ x_Q&y_Q&z_Q \\ x_R&y_R&z_R\\ \end{pmatrix}
Derive programmal kiszámoltattam, hogy a következő egyenlőség teljesül:
\displaystyle [BCD]⋅[DEF]⋅[FAB]⋅[ACE]-[ABC]⋅[CDE]⋅[EFA]⋅[BDF]=\frac{[ABCDEF]}{16}
Ezen számolás szerint az \displaystyle A, \displaystyle B, \displaystyle C, \displaystyle D, \displaystyle E, \displaystyle F pontosan akkor vannak egy kúpszeleten, ha a következő egyenlet teljesül:
\displaystyle [ABC]⋅[CDE]⋅[EFA]⋅[BDF]=[BCD]⋅[DEF]⋅[FAB]⋅[ACE]
Ezen bizonyítás szerint a kúpszelet lehet elfajuló is.
Annyi kérdésem van, hogy a "Derive"-s számolást "szépen" hogyan lehet elvégezni?
Amúgy a feladat nagyon tetszett, nagyon érdekes volt a feladat állítása, és nagyon tetszett a Kömal-ban közölt második megoldás.
|
|
| [1229] Tashi | 2025-01-12 18:44:58 |
 The theorem you are looking for is the Dedekind-Kummer theorem, also called Dedekind's criterion – I submitted a quite short solution to A. 892 using this theorem. It seems to be one of the most important theorems (both from mathematical and historical POV) taught in introductory Number Fields courses.
|
| Előzmény: [1224] marcius8, 2024-12-12 13:37:10 |
|
| [1228] BerkoErzsebet | 2025-01-12 01:13:29 |
 B. 5429. Egyik megoldásomban először arra jutottam, hogy elég 3 kúpszeletre belátni az állítást: origó középpontú 1 sugarú kör, y = x*x egyenletű parabola, illetve y = 1/x (x nem 0) hiperbola. Területaránytartó leképezésekkel bármelyik kúpszelet ezek egyikébe vihető. Kör. Én is a T=(abc)/(4R) képletet használtam. Háromszögterületet 3x3-as determinánsból számolok, ha adott a háromszög 3 csúcspontja. Ha A(a, a*a), B(b, b*b), C(c, c*c), akkor a háromszög területének (kétszerese) (c-b)*(a-b)*(a-c) (vagy az ellentettje). Könnyen kijött, mert a 3x3-as determináns Vandermonde determináns. A hiperbolánál majdnem ugyenez, csak le kell osztani (abc)-vel. Parabolánál, hiperbolánál mindkét oldalon ugyanazok vannak. (Körnél is.) Ezek után könnyen találtam 12 pontot, és 10-10 háromszöget, ahol hasonló állítást tudtam felírni. Úgy csináltam, hogy a 12 pont tisztességesen keveredjen, barátkozzon, tehát nem úgy, hogy 12=6+6.
|
|
|
| [1226] Lpont | 2024-12-12 16:18:04 |
 kieg: természetesen az átlagolandó számok mind pozitívak, mivel ABC hegyesszögű, a szögek koszinuszai pozitívak, így bármely két oldal négyzetösszege nagyobb a harmadik négyzeténél a koszinusz-tétel szerint.
|
| Előzmény: [1225] Lpont, 2024-12-12 15:18:58 |
|
| [1225] Lpont | 2024-12-12 15:18:58 |
 B.5418. egy lehetséges másik megoldása vázlatosan:
Vegyük a bizonyítandó egyenlőtlenség mindkét oldalának reciprokát, szorozzunk 3-mal, majd a bal oldalra alkalmazzuk a harmonikus és számtani közepek között egyenlőtlenséget.
Ekkor a jól ismert összefüggéshez jutunk, miszerint a háromszög oldalainak négyzetösszege kisebb vagy egyenlő, mint a köré írható kör sugara négyzetének kilencszerese.
|
|
| [1224] marcius8 | 2024-12-12 13:37:10 |
 A.892. Legyen \displaystyle \omega=\sqrt[3]{2}. Nevezzük Kömal-racionálisoknak a \displaystyle \bf{Q}(\omega) számokat, és nevezzük kömal-egészeknek a \displaystyle \bf{Z}(\omega) alakú számokat. Ekkor az \displaystyle a+b\omega+c\omega^2 alakú számok normája éppen az \displaystyle a^3+2b^3+4c^3-6abc. Ezek után arra gondoltam, hogy \displaystyle \bf{Z}(\omega)-ban mennyire lehet számelméletet összehozni, van-e ott is számelmélet alaptétele, hogyan lehet jellemezni a \displaystyle \bf{Z}(\omega)-beli prímeket vagy felbonthatatlanokat? És ezek után ezt a feladatot meg lehet-e oldani a \displaystyle \bf{Z}(\omega)-beli számelmélet alaptételével? Persze, lehet, hogy rossz az elképzelésem, de amikor megláttam ezt a feladatot, rögtön ezekre gondoltam.
|
|
| [1223] S.Ákos | 2024-11-16 00:21:17 |
 Egyszeruen lathato, hogy barmilyen haromszogre letezik kivulrol erinto kor. Hasznald a hivatalos megoldasbeli inverziot egy altalanos haromszogben, azt hogy harom egymast erinto kort egy kor vagy csak belulrol vagy csak kivulrol erint es hogy egy inverzio kozeppontjat nem tartalmazo kor kepe inverzio kozeppontjat nem tartalmazo kor. Az, hogy mikor van csak 1 mindharmat erinto kor (es egy egyenes, ami mindharmat erinti) es mikor van 2 mindharmat kivulrol erinto, a Descartes (kissing circles) tetelbol olvashato le, es az elobbi a tipikus bevezeto sangaku-feladat kicsit mashogy elmondva.
|
| Előzmény: [1222] marcius8, 2024-11-14 20:47:29 |
|
| [1222] marcius8 | 2024-11-14 20:47:29 |
 Még mindig a B.5410-es feladaton pampogok. Tehát a tetszőleges \displaystyle ABC háromszög \displaystyle A, \displaystyle B, \displaystyle C csúcsaiba megszerkesztjük az \displaystyle r_A=s-a, \displaystyle r_B=s-b, \displaystyle r_C=s-c sugarú \displaystyle k_A, \displaystyle k_B, \displaystyle k_C köröket, amelyek kívülről érintik egymást. Milyen egyszerű feltételt lehet adni arra, hogy létezzen olyan \displaystyle k_{kölső} kör, amely kívülről érinti a \displaystyle k_A, \displaystyle k_B, \displaystyle k_C köröket?
|
|
| [1221] S.Ákos | 2024-11-14 19:19:53 |
 Hasznos ezeknel a feladatoknal, ha nevet is rendelunk hozza, Soddy-koroknek hivjak ezeket. Az ilyen sangaku-szeru feladatoknal a Descartes-tetelt is erdemes lehet ismerni (bar joval kisebb korben alkalmazhato, mint az inverzio, 4 egymást paronkent erinto kor nem szerepel annyira gyakran).
|
| Előzmény: [1220] marcius8, 2024-11-14 18:35:15 |
|
| [1220] marcius8 | 2024-11-14 18:35:15 |
 B.5410 feladatban Geogebra programot csináltam tetszőleges \displaystyle ABC háromszögre:
\displaystyle s=\frac{+a+b+c}{2}
\displaystyle r_A=s-a, \displaystyle k_A=kör(\displaystyle A, \displaystyle r_A),
\displaystyle r_B=s-b, \displaystyle k_B=kör(\displaystyle B, \displaystyle r_B),
\displaystyle r_C=s-c, \displaystyle k_C=kör(\displaystyle C, \displaystyle r_C),
\displaystyle rrrr=0+r_A^2*r_B^2+r_B^2*r_C^2+r_C^2*r_A^2-2r_Ar_Br_C(r_A+r_B+r_C)
\displaystyle r_{belső}=r_Ar_Br_C(0-2(r_Ar_Br_Cs)^{1/2}+(r_Br_C+r_Cr_A+r_Ar_B))/rrrr
\displaystyle r_{külső}=r_Ar_Br_C(0-2(r_Ar_Br_Cs)^{1/2}-(r_Br_C+r_Cr_A+r_Ar_B))/rrrr
\displaystyle x_A=A*(1,0), \displaystyle y_A=A*(0,1) az \displaystyle A csúcs \displaystyle x és \displaystyle y koordinátája.
\displaystyle x_B=B*(1,0), \displaystyle y_B=B*(0,1) a \displaystyle B csúcs \displaystyle x és \displaystyle y koordinátája.
\displaystyle x_C=C*(1,0), \displaystyle y_C=C*(0,1) a \displaystyle C csúcs \displaystyle x és \displaystyle y koordinátája.
\displaystyle t=2x_A(y_B-y_C)+2x_B(y_C-y_A)+2x_C(y_A-y_B), ez az \displaystyle ABC háromszög előjeles területének négyszerese.
\displaystyle ux=a*b*(x_A-x_B)+b*c(x_B-x_C)+c*a(x_C-x_A)
\displaystyle uy=a*b*(y_A-y_B)+b*c(y_B-y_C)+c*a(y_C-y_A)
\displaystyle vx=2a*(x_B-x_C)+2b*(x_C-x_A)+2c*(x_A-x_B)
\displaystyle vy=2a*(y_B-y_C)+2b*(y_C-y_A)+2c*(y_A-y_B)
\displaystyle wx=(x_A^2+y_A^2)*(x_B-x_C)+(x_B^2+y_B^2)*(x_C-x_A)+(x_C^2+y_C^2)*(x_A-x_B)
\displaystyle wy=(x_A^2+y_A^2)*(y_B-y_C)+(x_B^2+y_B^2)*(y_C-y_A)+(x_C^2+y_C^2)*(y_A-y_B)
\displaystyle x_{belső}=(+r_{belső}*vy-uy+wy)/t,
\displaystyle y_{belső}=(-r_{belső}*vx+ux-wx)/t,
\displaystyle P_{belső}=(x_{belső}, y_{belső}),
\displaystyle k_{belső}=kör(\displaystyle P_{belső}, r_{belső}),
\displaystyle x_{külső}=(-r_{külső}*vy-uy+wy)/t,
\displaystyle y_{külső}=(+r_{külső}*vx+ux-wx)/t,
\displaystyle P_{külső}=(x_{külső}, y_{külső}),
\displaystyle k_{külső}=kör(\displaystyle P_{külső}, r_{külső}),
|
|
| [1219] marcius8 | 2024-11-14 17:32:49 |
 A B.5409 feladatban először arra gondoltam, hogy mennyi az \displaystyle A*B események valószínűsége. Először arra gondoltam, hogy ha \displaystyle A és \displaystyle B események egymástól függetlenek lennének, akkor igazából elég csak az \displaystyle A és \displaystyle B események valószínűségét kiszámolni. De kiderült, hogy az \displaystyle A és \displaystyle B események nem lehetnek függetlenek. Legyen az \displaystyle A*B esemény valószínűsége \displaystyle k/32!, ahol \displaystyle k az \displaystyle A*B esemény "kedvező eseteinek" száma, azaz \displaystyle k egész szám. Ha \displaystyle A és \displaystyle B események függetlenek lennének, akkor a \displaystyle p(A*B)=p(A)*p(B) egyenlőségből, továbbá a \displaystyle p(A)=\frac{(8!)^4(4!)^8}{32!}, \displaystyle p(B)=\frac{(4!)^8(8!)^4}{32!}, és a \displaystyle p(A*B)=\frac{k}{32!} egyenlőségekből \displaystyle k=\frac{(8!)^4(4!)^8*(4!)^8(8!)^4}{32!} összefüggés következne, ami nem lehet, mert a \displaystyle k egész szám, ugyanakkor a \displaystyle \frac{(8!)^4(4!)^8*(4!)^8(8!)^4}{32!} tört nem lehet egész szám, mert a nevezőben olyan szorzat van, amelyben van pl. 31-es prímtényező, és a számlálóban olyan szorzat van, amelyben nincs a 31-es prímtényező. Amit viszont nagyon szeretnék tudni, az az, hogy akkor mennyi a \displaystyle p(A*B) valószínűség, előre is köszönöm mindenki segítségét.
|
|
| [1218] marcius8 | 2024-11-14 17:06:11 |
 A B.5413 feladatot vaddisznó módjára, azaz mindenféle gondolkodás nélkül csak számolással csináltam. Az \displaystyle MS^2−IS^2−IM^2>0.egyenlőtlenségben a háromszög \displaystyle a, \displaystyle b, \displaystyle c oldalainak segítségével kiszámoltam az \displaystyle MS^2, \displaystyle IS^2, \displaystyle IM^2 mennyiségeket. Bár ezek nem igazán egyszerűek voltak, az \displaystyle MS^2−IS^2−IM^2 mennyiségre a következő kifejezés adódott, ahol \displaystyle s a háromszög félkerülete:
\displaystyle MS^2−IS^2−IM^2=\frac{+(s-a)(b-c)^2+(s-b)(c-a)^2+(s-c)(a-b)^2}{3s}
Ebből az összefüggésből az \displaystyle MS^2−IS^2−IM^2>0 egyenlőtlenség nyilvánvalóan adódik. Geogebrával ellenőriztem ezt az eredményt.
A megoldásban közölt megjegyzés szerint: így végül \displaystyle MO^2, \displaystyle IO^2, \displaystyle IM^2 mindegyikére elegáns formula adható \displaystyle R, \displaystyle r, \displaystyle ϱ segítségével, ahol \displaystyle R a háromszög köré írt kör sugara, \displaystyle r a háromszögbe írt kör sugara, \displaystyle ϱ a talpponti háromszögbe írt kör sugara. Ha lesz szabadidőm, megpróbálom megtalálni ezeket az összefüggéseket.
|
|
| [1217] Lpont | 2024-11-13 15:48:19 |
 A C.1825. feladat honlapon olvasható megoldása talán kiegészíthető néhány diszkussziós mondattal arra az esetre, ha a kisebbik kör belülről érinti a nagyobbikat.
|
|
| [1216] Sinobi | 2024-10-14 18:57:01 |
 Fizikában is gyakran hasznos ha valós számokkal számolsz. Ha eddig direkt elkerülted a tanárod tanácsára, érdemes lehet visszarakni a repertoárodba. A valós számoknak van egy csomó jó tulajdonságuk, amiket ki tudsz használni időről időre. Például téridő geometriában, amit említettél, össze lehet adni az időt a távolsággal, anélkül hogy a dimenziókat és a mértékegység váltó jeleket végig cipelned kéne minden egyes képletben. Legyen S egy inerciarendszer, jelölje t,x,y,z a pozíciókhoz tartozó valós számokat, stb.
Amúgy igen, B.5402-t ha megnézi egy fizikus, annak a "háromszög oldalainak hosszúsága" nem egy valós szám, hanem egy hosszúság dimenziójú mennyiség, így a "tegyük fel hogy fennáll" egyenlet soha nem áll fenn, és a feladat triviális.
|
|








