Beszámoló a 42. Nemzetközi Matematikai Diákolimpiáról

Az idei Nemzetközi Matematikai Diákolimpiát Washingtonban, az Egyesült Államok fővárosában rendezték meg július 1. és 14. között 83 ország 473 diákjának részvételével. Az országok általában hattagú csapatokkal vettek részt, ha a csapatlétszám ennél kisebb volt, az alábbi felsorolásban az országnév után zárójelben jelzem a versenyzők számát. A résztvevők listája:

Albánia (5), Amerikai Egyesült Államok, Argentína, Ausztrália, Ausztria, Azerbajdzsán (3), Belgium, Belorusszia, Bosznia-Hercegovina, Brazília, Bulgária, Ciprus, Csehország, Dánia, Dél-Afrika, Dél-Korea, Ecuador, Észtország, Finnország, Franciaország, Fülöp-szigetek, Görögország, Grúzia, Guatemala (3), Hollandia, Hongkong, Horvátország, India, Indonézia, Irán, Írország, Izland, Izrael, Japán, Jugoszlávia, Kanada, Kazahsztán, Kína, Kirgizisztán (5), Kolumbia, Kuba, Kuvait (4), Lengyelország, Lettország, Litvánia, Luxemburg (2), Macao, Macedónia, Magyarország, Malajzia, Marokkó, Mexikó, Moldova (5), Mongólia, Nagy-Britannia, Németország, Norvégia, Olaszország, Oroszország, Örményország (5), Paraguay (5), Peru, Portugália, Románia, Spanyolország, Sri Lanka (4), Svájc, Svédország, Szingapúr, Szlovákia, Szlovénia, Tajvan, Thaiföld, Törökország, Trinidad és Tobago, Tunézia, Türkmenisztán (5), Új-Zéland, Ukrajna, Uruguay (2), Üzbegisztán, Venezuela (5), Vietnam.

A versenyen szokás szerint mindkét napon négy és fél óra alatt 3-3 feladatot kellett megoldani. (A feladatokat alább közöljük.) Mindegyik feladat helyes megoldásáért 7 pont járt, így egy versenyző maximális teljesítménnyel 42 pontot szerezhetett. (Ez egyébként négy versenyzőnek sikerült: két kínainak és két amerikainak.)

Idén a feladatok meglehetősen nehéznek bizonyultak, ennek megfelelően az egyes díjak ponthatára elég alacsony volt. Aranyérmet 30-42 ponttal, ezüstérmet 20-29 ponttal, bronzérmet pedig 11-19 ponttal lehetett szerezni.

A magyar csapatból

Harangi Viktor

Csóka Endre (Debrecen, Fazekas M. Gimn., 10. o.t.) pedig 21 ponttal ezüstérmet, míg

Kovács Erika (Fazekas M. Főv. Gyak. Gimn., 11. o.t.) és

Vörös László (Győr, Révai M. Gimn., 12. o.t.) egyaránt 19 ponttal,

Csikvári Péter (Fazekas M. Főv. Gyak. Gimn., 11. o.t.) pedig 14 ponttal bronzérmet nyertek.

A hatodik versenyző,

Horváth Illés

A csapat vezetője Pelikán József (ELTE, Algebra és Számelmélet Tanszék), helyettes vezetője Dobos Sándor (Fazekas M. Főv. Gyak. Gimn.) volt.

Az országok (nem-hivatalos) pontversenyét Kína toronymagasan nyerte. Magyarország idén a 21. lett, ami rosszabb, mint az évek óta megszokott eredmények. Tudomásul kell azonban venni, hogy a mezőny egyre erősebb, és sok ország komoly összegeket áldoz a versenyzők felkészítésére.

Következzék a csapatverseny első 30 helyezettjének listája, pontszámaik feltüntetésével:

1.	Kína	225
2-3.	Oroszország és USA	196
4-5.	Bulgária és Dél-Korea	185
6.	Kazahsztán	168
7.	India	148
8.	Ukrajna	143
9.	Tajvan	141
10.	Vietnam	139
11.	Törökország	136
12.	Belorusszia	135
13.	Japán	134
14.	Németország	131
15.	Románia	129
16.	Brazília	120
17.	Izrael	113
18.	Irán	111
19-20.	Hongkong és Lengyelország	107
21.	Magyarország	104
22-23.	Argentína és Thaiföld	103
24.	Kanada	100
25.	Ausztrália	97
26.	Kuba	92
27.	Üzbegisztán	91
28.	Franciaország	88
29.	Szingapúr	87
30.	Görögország	86.

A versenyzők felkészítésében Dobos Sándor mellett oroszlánrészt vállalt Reiman István, aki ezt a munkát már több mint 40 éve csinálja. Ezúton szeretnék köszönetet mondani neki.

Az egyes versenyzők tanárai a következők voltak:

Fazakas Tünde, Táborné Vincze Márta

Csóka Endre: Balázs Tivadar, Pósa Lajos, Reiman István, Páles Zsolt

Harangi Viktor: Fazakas Tünde, Táborné Vincze Márta, Pósa Lajos

Horváth Illés: Fazakas Tünde, Táborné Vincze Márta

Kovács Erika: Fazakas Tünde, Táborné Vincze Márta, Pósa Lajos

Vörös László: Zábrádiné Schmierer Emília, Zsebők Ottó

A versenyről elmondható, hogy összességében jól rendezett volt. A vendéglátók kirándulásokat szerveztek a résztvevőknek (diákoknak többet, tanároknak kevesebbet). A záróünnepség a John F. Kennedy Kulturális Központban zajlott, aminek impozáns, új épülete közvetlenül a Potomac folyó partján fekszik.

A záróünnepség fényét nagymértékben emelte, hogy az aranyérmeseknek a díjat a világhírű matematikus, Andrew Wiles (a Fermat-tétel bizonyítója) adta át. A magyar csapatnak a záróbanketten sikerült megörökíttetnie magát Andrew Wiles társaságában.

Balról jobbra: Vörös László, Csíkvári Péter, Harangi Viktor, Pelikán József, Csóka Endre, Andrew Wiles, Dobos Sándor, Horváth Illés, Kovács Erika Renáta

A jövő évi diákolimpiát Skóciában, Glasgow-ban rendezik július 18. és 31. között.

Pelikán József

A 42. Nemzetközi Matematikai Diákolimpia feladatai

Első nap

1. Legyen az ABC hegyesszögű háromszög körülírt körének középpontja O. Legyen P az A-ból induló magasságvonal talppontja a BC oldalon.

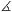Tegyük fel, hogy BCA$\displaystyle szog$ $ge$ ABC $szog$ +30^o.

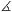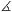Bizonyítsuk be, hogy CAB $szog$ +COP $szog$ <90^o.

2. Bizonyítsuk be, hogy

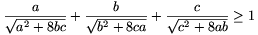
${a\over\sqrt{a^2+8bc}}+{b\over\sqrt{b^2+8ca}}+{c\over\sqrt{c^2+8ab}}\ge1$

minden a, b, c pozitív valós számra.

3. Egy matematikaversenyen 21 lány és 21 fiú vett részt.

Mindegyik versenyző legfeljebb hat feladatot oldott meg.
Mindegyik fiúhoz és mindegyik lányhoz van legalább egy olyan feladat, amelyet mindketten megoldottak.

Bizonyítsuk be, hogy van olyan feladat, amelyet legalább három lány és legalább három fiú megoldott.

Második nap

4. Legyen n egy 1-nél nagyobb páratlan egész, k₁, k₂, ..., k_n pedig adott egészek. Az 1, 2, ..., n számok mind az n! darab a=(a₁, a₂, ..., a_n) permutációjára legyen

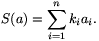
$S(a)=\sum\limits_{i=1}^nk_ia_i.$

Bizonyítsuk be, hogy van két olyan b és c permutáció, amelyekre b $ne$ c, és n! osztója (S(b)-S(c))-nek.

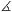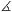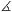5. Az ABC háromszögben legyen AP a BAC $szog$ szögfelezője, ahol P a BC oldalon van, BQ pedig az ABC $szog$ szögfelezője, ahol Q a CA oldalon van. Tudjuk, hogy BAC $szog$ =60^o és hogy AB+BP=AQ+QB.

Mik az ABC háromszög szögeinek lehetséges értékei?

6. Legyenek a, b, c, d egészek, amelyekre a>b>c>d>0. Tegyük fel, hogy

ac+bd=(b+d+a-c)(b+d-a+c).

Bizonyítsuk be, hogy ab+cd nem prímszám.

Már regisztráltál?
Új vendég vagy?