A 32. Nemzetközi Fizikai Diákolimpia feladatai

(A feladatok megoldását a novemberi számunkban közöljük.)

Kísérleti forduló

A mérési feladat kidolgozására 5 óra állt a versenyzők rendelkezésére.

Forgó folyadék

A mérés három fő részből áll:

1. A forgó folyadék szabad felszínének vizsgálata, és a nehézségi gyorsulás meghatározása.

2. A forgó folyadéknak mint optikai rendszernek a vizsgálata.

3. A folyadék törésmutatójának meghatározása.

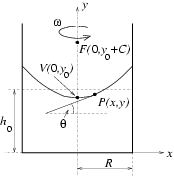
1. ábra. Definíciók: y tengely körüli állandó szögsebességű forgás esetében $\displaystyle theta$ a lejtés szöge a P(x, y) pontban; V a forgó folyadék forgásparaboloid felületének csúcspontja, F a fókusza. A folyadék eredeti magassága h₀, R pedig az edény sugara.

Ha egy folyadékkal töltött hengeres edény a középpontján átmenő függőleges tengely körül állandó $\displaystyle omega$ szögsebességgel forog, a folyadék szabad felszíne forgásparaboloid alakú lesz (1. ábra). Egyensúlyi állapotban a felület P(x, y) pontbeli érintője $\displaystyle theta$ szöget zár be a vízszintessel, úgy hogy

(1)	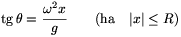$\tg\theta={\omega^2x\over g}\qquad{\rm(ha}\quad\|x\|\le R{\rm)}$

ahol R az edény sugara és g a nehézségi gyorsulás. Az is belátható, hogy $\displaystyle omega$<$\displaystyle omega$_max esetében (ahol $omega$ _max ebben a részfeladatban azt a szögsebességet jelöli, amelynél a forgó folyadék felszíne középen érinti az edény alját) az

(2)	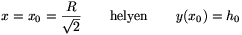$x=x_0={R\over\sqrt{2}}\qquad{\rm helyen}\qquad y(x_0)=h_0$

azaz a forgó folyadék magassága megegyezik az álló folyadék magasságával.

A forgó folyadék szabad felszíne parabola alakú, amit a következő egyenlet definiál:

(3)	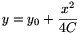$y=y_0+{x^2\over4C}$

ahol a parabola csúcspontja a V(0, y₀) pontban, fókusza pedig az F(0, y₀+C) pontban van. Ha a szimmetriatengellyel (optikai tengellyel) párhuzamos fénysugarak verődnek vissza a parabola felszínéről, akkor ezek mind átmennek az F ponton.

A mérési berendezés és tartozékai (2. ábra)

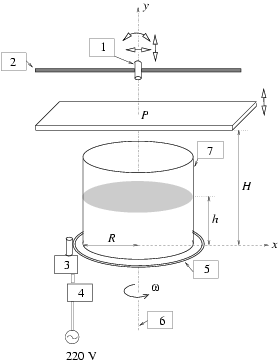
2. ábra. Kísérleti elrendezés az 1. és a 2. részfeladathoz: 1. Állványra rögzített lézer, 2. átlátszó ernyő, 3. motor, 4. motor szabályozó, 5. forgó korong, 6. forgástengely, 7. hengeres edény.

-- Glicerinnel töltött, merev, hengeres műanyag edény. Az edény oldalán és alján milliméter skála van.

-- Kis egyenáramú motorral hajtott forgó korong. A motort egy változtatható feszültségforrás működteti, ezzel lehet szabályozni a szögsebességet.

-- Átlátszó vízszintes ernyő, amelyre átlátszó vagy áttetsző milliméter skálát rakhatsz. Az ernyő helyzete függőleges és vízszintes irányban is állítható.

-- Állványra szerelt lézer. A lézer helyzete állítható. A lézer fejrésze cserélhető.

-- Másik fejrész a lézerhez.

-- Vonalzó.

-- Filctoll.

-- Stopper. (A bal gombbal lehet nullázni, a középsővel az üzemmódot beállítani, a jobb gombbal pedig indítani és leállítani a stoppert.)

-- 1000 vonal/mm-es optikai rács.

-- Buborékos vízszintező.

-- Szemüveg.

Fontos figyelmeztetések

NE NÉZZÉL KÖZVETLENÜL A LÉZERSUGÁRBA! VEDD FIGYELEMBE, HOGY A TÜKRÖZŐ FELÜLETEKRŐL VISSZAVERŐDŐ LÉZERFÉNY IS VESZÉLYES LEHET! SAJÁT BIZTONSÁGOD ÉRDEKÉBEN HASZNÁLD A RENDELKEZÉSRE BOCSÁTOTT SZEMÜVEGET!

A mérés során végig óvatosan bánj a glicerinnel teli edénnyel!

A forgó korong vízszintezve van. A buborékos vízszintezőt az ernyő vízszintezésére használd!

A mérés során az ernyőn több fényfoltot is fogsz látni, melyeket a folyadék, a levegő, az ernyő és az edény különböző határfelületein létrejövő visszaverődések és/vagy törések okoznak. Győződj meg róla, hogy a megfelelő sugarat méred-e!

A folyadék forgatásakor folyamatosan változtasd a szögsebességet, és várd meg az egyensúlyi állapot beálltát, mielőtt mérni kezdenél!

A mérés

1. rész: g Meghatározása forgó folyadék segítségével (7,5 pont)

-- Vezesd le az (1)-es egyenletet!

-- Mérd meg az edényben lévő folyadék h₀ magasságát és az edény 2R belső átmérőjét!

-- Helyezd az ernyőt a fényforrás és az edény közé! Mérd meg az ernyő és a forgó asztal közti H távolságot.

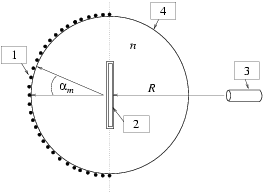
-- Állítsd be a lézert úgy, hogy a fénysugár függőlegesen lefelé mutasson, és a folyadék felszínét az edény középpontjától 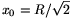$x_0=R/\sqrt{2}$ távolságra érje el!

-- Forgasd lassan a forgó asztalt! Győződj meg róla, hogy a folyadék középpontja nem éri el az edény alját!

-- Tudjuk, hogy $\displaystyle x_0=R/\sqrt{2}$ esetén a folyadék magassága az $omega$ szögsebeségtől függetlenül ugyanakkora, mint az eredeti h₀ magasság. Felhasználva ezt a tényt mérd meg ezen az x₀ helyen a $\displaystyle theta$ szöget különböző $omega$ szögsebességeknél, hogy ebből majd a g nehézségi gyorsulást meghatározhasd!

-- Foglald táblázatba az egyes $\displaystyle omega$ értékeknél mért és számított mennyiségeket!

-- Készítsd el a g meghatározásához szükséges grafikont!

-- Számítsd ki g értékét és határozd meg a mérési hibát!

-- Írd be 2R, x₀, h₀, és H értékét, valamint g mért értékét és hibáját a válaszlapra!

2. rész: Optikai rendszer

A kísérlet ezen részében a forgó folyadékot képalkotó optikai rendszernek tekintjük. Mivel a forgás szögsebessét változtatva a felület görbülete változik, az optikai eszközünk fókusztávolsága függ $\displaystyle omega$-tól. a)

A fókusztávolság vizsgálata (5,5 pont)

-- Állítsd a lézert olyan helyzetbe, hogy a lézersugár az edény tengelye mentén függőlegesen lefele haladjon! Jelöld meg azt a P pontot, ahol a fénysugár átmegy az ernyőn. Ezt a pontot az edény középpontjával összekötő egyenes a rendszer optikai tengelye.

-- Mivel a folyadék felszíne parabolatükörként viselkedik, az optikai tengellyel párhuzamosan beeső fénysugarak a visszaverődésük után az optikai tengelyt az F fókuszpontban metszik.

-- Állítsd be a forgás szögsebességét úgy, hogy a fókuszpont éppen az ernyőre kerüljön. Mérd meg ekkor a forgás $omega$ szögsebességét, valamint az ernyő és a forgó korong közötti H távolságot!

-- Ismételd meg a fenti lépéseket különböző H értékek mellett!

-- Másold át 2R és h₀ mért értékeit, valamint a különböző H értékekhez tartozó mért $omega$ -kat a válaszlapra!

-- Mérési adataidra illesztett alkalmas grafikon segítségével határozd meg, hogy milyen kapcsolat van a fókusztávolság és a szögsebesség között! b)

Az ernyőn látható ,,kép'' analízise (3,5 pont)

A mérési feladat ezen részében az optikai rendszer által létrehozott ,,képet'' kell vizsgálnod. Ezt az alábbi lépéseket követve teheted meg.

-- Az óramutató járásával ellentétesen csavarva távolítsd el a lézer fejrészét!

-- Helyezd fel (az óramutató járásával egyezően csavarva) a borítékban található új fejrészt! Így most a lézered a korábbi keskeny nyaláb helyett egy jellegzetes alakban kiinduló fényt fog kibocsátani.

-- Állítsd be a lézert oly módon, hogy a fénye nagyjából az edény közepénél, majdnem merőlegesen essék a folyadékra!

-- Helyezz egy áttetsző papírlapot az edényhez közeli helyzetben rögzített vízszintes ernyőre oly módon, hogy a lézerfény ne haladjon át a papírlapon, de a visszavert fény már igen!

-- Figyeld meg a fényforrás direkt fénye által létrehozott, valamint a még nem forgó folyadékról visszaverődött fény által létrehozott ,,kép'' méretét, valamint állását!

-- Kezdd el forgatni a folyadékot, és lassan növeld a szögsebességet egészen a feszültségforrás által elérhető legnagyobb értékig, s eközben figyeld az ernyőt! Miközben $omega$ -t növeled, több szögsebesség-intervallumot figyelhetsz meg, amelyekben a ,,kép'' jellemző tulajdonságai lényegesen különbözőek. Írd le ezeket a megfigyeléseket (egészítsd ki a válaszlap táblázatát az egyes frekvencia-intervallumokra utaló sorok hozzáadásával)!

3. rész: A törésmutató (3,5 pont)

A mérési feladat ezen részében az adott folyadék törésmutatóját határozzuk meg egy optikai rács segítségével. Ha $lambda$ hullámhosszúságú monokromatikus fény merőlegesen esik egy diffrakciós rácsra, az m-edrendű elhajlási maximum $alpha$ _m szögét megadó egyenlet:

(4)	m$\displaystyle lambda$=dsin$\displaystyle alpha$_m,

ahol d a rácsállandó. Ebben a részfeladatban egy diffrakciós rács segítségével a lézerfény hullámhosszát, majd a folyadék törésmutatóját kell meghatároznod (3. ábra).

3. ábra. Az optikai rács felülnézetben. 1. Skálázott oldalfal, 2. optikai rács tartóban, 3. lézer, 4. hengeres edény.

-- Határozd meg az optikai rács segítségével a lézerfény hullámhosszát!

-- Merítsd a rácsot az edény közepénél függőlegesen a folyadékba!

-- Irányítsd a lézert az eredeti fejrésszel úgy, hogy a fénye az edény oldalfalán keresztül merőlegesen essék a rácsra!

-- Az edény túloldalára erősített milliméter-skálán figyeld meg a keletkező elhajlási képet! Ha szükséges, végezz távolságméréseket!

-- A mérési adataid felhasználásával számítsd ki a folyadék n törésmutatóját! (A műanyag edény falának a fény útjára gyakorolt hatását elhanyagolhatod.)

Elméleti forduló

Az elméleti feladatok kidolgozására 5 óra állt a versenyzők rendelkezésére. Megoldásaikat előre elkészített VÁLASZLAPOK megfelelő rovatainak kitöltésével kellett megadniuk, elsősorban rajzok, képletek, formulák és (a feladat egyéb adatai által indokolt pontosságú) számszerű eredmények formájában. A hosszabb szöveges magyarázat mellőzését kérték a rendezők.

1. feladat.

Ez a feladat 4 független részfeladatból áll.

1.A. Klisztron

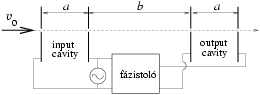
4. ábra.

A klisztron nagyon nagy frekvenciás jelek erősítésére szolgáló eszköz. A klisztron lényegében két egyforma lemezpárból (üregből) áll, melyek egymástól b távolságra vannak a 4. ábrán látható módon.

Egy kezdetben v₀ sebességű elektronsugár halad át az egész rendszeren a lemezekre vágott kicsiny lyukakon keresztül. Az erősítendő nagyfrekvenciás feszültséget egy meghatározott fáziskülönbséggel (a T periódusidő 2$\displaystyle pi$ fázisnak felel meg) rákapcsolják mindkét lemezpárra, ezáltal az üregekben vízszintes, váltakozó elektromos tér keletkezik. Azok az elektronok, amelyek akkor lépnek be a bal oldali üregbe (input cavity), amikor az elektromos térerősség vektora jobbra mutat, lelassulnak, és fordítva: a balra mutató elektromos térbe érkező elektronok felgyorsulnak. Így a továbbhaladó elektronok bizonyos távolságra összetorlódnak. Ha a jobb oldali üreg (output cavity) éppen egy torlódási pontnál van, az üregben levő elektromos tér energiát kap az elektronsugártól, feltéve, hogy az elektromos tér fázisa megfelelő.

Legyen a feszültségjel egy négyszögjel T=1,0^.10^-9 s periódusidővel váltakozva V=$\displaystyle pm$0,5 V feszültségek között! Az elektronok kezdeti sebessége v₀=2,0^.10⁶ m/s, fajlagos töltése pedig e/m=1,76^.10¹¹ C/kg. Az a távolság olyan kicsi, hogy az elektronok üregen való áthaladási ideje elhanyagolható. Számítsd ki, és add meg 4 értékes jegy pontossággal a következőket:

a) Azt a b távolságot, ahol az elektronok összetorlódnak. (1,5 pont)

b) A fázistoló által létrehozandó fáziskülönbséget. (1 pont)

1.B. Molekulák közötti távolság

Jelölje d_L a vízmolekulák közti átlagos távolságot, d_V pedig a vízgőz molekuláinak átlagos távolságát! Feltételezzük, hogy mindkét fázis 100 ^oC-os és légköri nyomású, továbbá azt, hogy a vízgőz ideális gázként viselkedik! Számítsd ki az alábbi adatok felhasználásával a d_V/d_L arányt! (2,5 pont)

Adatok:

A víz sűrűsége folyadékfázisban: $\displaystyle varrho$_L=1,0^.10³ kg/m³.

A víz móltömege: M=1,8^.10^-2 kg/mol.

A légköri nyomás: p₀=1,0^.10⁵ N/m².

Az univerzális gázállandó: R=8,3 J/mol^.K.

Az Avogadro-szám: N_A=6,0^.10²³/mol.

1.C. Egyszerű fűrészfog-generátor

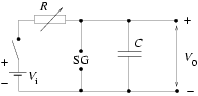
5. ábra.

Egy fűrészfog alakú feszültségjel (V₀) az 5. ábrán látható C kapacitással, R változtatható ellenállással, V_i ideális teleppel és az SG jelű szikraközzel (spark gap) állítható elő. Ez utóbbi két elektródát tartalmaz, melyek távolsága változtatható. Ha az elekródák közötti feszültség eléri a V_f kisülési (firing) feszültséget, a közöttük levő levegő átüt, így a szikraköz rövidzárként működik mindaddig, míg a rá eső feszültség nagyon kis értékre nem csökken.

a) Rajzold fel, hogyan változik a kapcsoló zárását követően a V₀ feszültség a t idő függvényében! (0,5 pont)

b) Milyen feltételnek kell teljesülnie ahhoz, hogy V₀ csaknem lineárisan változó fűrészfogjel legyen? (0,2 pont)

c) Feltéve, hogy ez a linearitási feltétel teljesül, vezesd le a jelalak T periódusidejét megadó egyszerű közelítő formulát! (0,4 pont)

d) Mit változtassunk meg (R-t és/vagy SG-t) ahhoz, hogy a fűrészfogjelnek csak a periódusideje változzék? (0,2 pont)

e) Mit változtassunk meg (R-t és/vagy SG-t) ahhoz, hogy a fűrészfogjelnek csak az amplitúdója változzék? (0,2 pont)

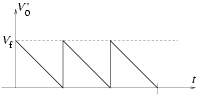
6. ábra.

f) Kapsz a korábbi eszközök mellé még egy változtatható kimenetű egyenáramú feszültségforrást is. Tervezz meg és rajzolj le egy olyan új áramkört, mellyel a 6. ábrán látható feszültség-jelalakot állíthatod elő! (1 pont)

1.D. Atomsugár

Egy atomsugarat úgy lehet előállítani, hogy bizonyos számú atomból álló gázt T hőmérsékletre hevítünk, és lehetővé tesszük, hogy az atomok a kemence falán lévő igen kicsiny (az atomok méretével összemérhető) D átmérőjű lyukon vízszintes irányban kilépjenek (7. ábra).

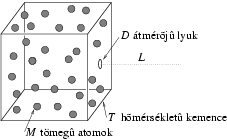
7. ábra.

Becsüld meg, mekkorára nő a sugár átmérője L hosszúságú vízszintes út megtétele után! Az atomok tömege M. (2,5 pont)

2. feladat. Kettőscsillag

a) Jól ismert, hogy a legtöbb csillag kettőscsillag-rendszernek része. A kettőscsillagok egyik típusa egy m₀ tömegű és R sugarú közönséges csillagból, valamint egy kisméretű, de sokkal nagyobb tömegű (M tömegű) neutroncsillagból áll, és ezek egymás körül keringenek. A Föld mozgását a továbbiakban mindenhol figyelmen kívül hagyhatod! Egy ilyen kettőscsillagról távcsöves megfigyelésekkel a következő információkat nyerhetjük:

-- A csillag legnagyobb szögelmozdulása 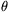$Delta$ $theta$ , míg a neutroncsillag legnagyobb szögelmozdulása $Delta$ $phi$ (8. ábra).

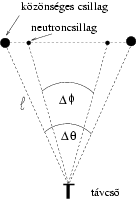
8. ábra.

-- A legnagyobb szögelmozduláshoz szükséges idő $tau$ .

-- A közönséges csillagra jellemző sugárzás vizsgálata azt mutatja, hogy a csillag felszíni hőmérséklete T, és róla a Föld felszínére felületegységenként és időegységenként P sugárzási energia érkezik.

-- Ebben a sugárzásban a kalcium színképvonalának hullámhossza $Delta$ $lambda$ értékkel különbözik a földi körülmények között szokásos $lambda$ ₀ hullámhossztól. Az eltérést a közönséges csillag gravitációs terének hatása okozza. (A számítás során a fotont h/(c $lambda$ ) effektív tömegű részecskének tekintheted.)

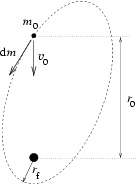
9. ábra.

1 Vezess le egy olyan kifejezést, amely a távcsöves megfigyelési adatok és univerzális állandók felhasználásával megadja a Föld és a kettőscsillag $\displaystyle ell$ távolságát. (7 pont)

b) Tegyük fel, hogy M$\displaystyle gg$m₀, és így a közönséges csillag lényegében a neutroncsillag körül kering egy r₀ sugarú körpályán. Feltesszük továbbá, hogy a közönséges csillag gázt bocsát ki magából, s ezt a gázt saját magához képest v₀ relatív sebességgel a neutroncsillag felé lövelli (9. ábra). Tudva azt, hogy a feladatban a neutroncsillag gravitációs erőtere a meghatározó, és elhanyagolva a közönséges csillag pályájának megváltozását, határozd meg azt az r_f távolságot, amennyire a gáz megközelíti a neutroncsillagot. (3 pont)

3. feladat. Magnetohidrodinamikai (MHD) generátor

Egy téglalap keresztmetszetű, vízszintes műanyag cső szélessége w, magassága h. Az önmagába záródó csőben $varrho$ fajlagos ellenállású higany található. A higanyt egy P túlnyomást biztosító szivattyú állandó v₀ sebességgel hajtja körbe. A cső két szemközti függőleges falának L hosszúságú szakaszát rézlemezek borítják (10. ábra).

Egy folyadék valóságos mozgása nagyon bonyolult, összetett jelenség. A helyzet egyszerűsítése érdekében tegyük fel a következőket:

Jóllehet a folyadék viszkózus, a sebességet tekintsük a cső teljes keresztmetszetében ugyanakkorának!

A folyadék sebessége mindig arányos a folyadékra ható eredő külső erővel.

A folyadék összenyomhatatlan.

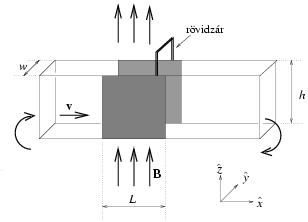
10. ábra.

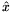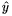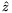A rézlapokat a folyadékon kívül rövidre zárjuk, majd folyadék rézlapokkal határolt szakaszán függőlegesen felfelé mutató, homogén B mágneses teret kapcsolunk be. Az elrendezést a 10. ábra mutatja, a megoldás során használandó $\hat x$ , $\hat y$ és $\hat z$ egységvektorokkal.

a) Határozd meg a mágneses tér által a folyadékra kifejtett erőt (L, B, h, w, $varrho$ és a megváltozott v sebesség függvényében)! (2 pont)

b) Vezess le egy olyan formulát, amely megadja a folyadék megváltozott v sebességét (v₀, P, L, B és $\displaystyle varrho$ függvényében) a mágneses tér bekapcsolása után! (3 pont)

c) Vezesd le azt a képletet, amely megadja, hogy mekkora többletteljesítményre van szüksége a szivattyúnak ahhoz, hogy az áramlás sebességét az eredeti v₀ értékre állítsa vissza! (2 pont)

d) A mágneses teret most kikapcsoljuk, és a higanyt v₀ sebességgel folyó vízzel helyettesítjük. Egy adott frekvenciájú elektromágneses hullámot küldünk végig az L hosszúságú szakaszon, az áramlással azonos irányban. A víz törésmutatója n, v₀$\displaystyle ll$c. Vezesd le azt a kifejezést, amely megadja, hogy mekkora a folyadék mozgásának járuléka a hullám L hosszúságú szakaszra eső fáziskülönbségéhez! (3 pont)

Beszámoló a 32. Nemzetközi Fizikai Diákolimpiáról

Már regisztráltál?
Új vendég vagy?