A modern matematikába, illetve a matematika XX-XXI. századi alkalmazásaiba pillanthatunk be neves egyetemi oktatók, kutatók segítségével. Mindig kedden, 16 órakor kezdődnek a diákok, tanárok és más érdeklődők számára meghirdetett programok a Fővárosi Fazekas Mihály Gimnázium Nagytermében.

Előadások ebben a tanévben:

2006. szeptember 19. Topológia
Moussong Gábor: A Poincaré sejtés

2006. november 21.
Pelikán József: Konstansok

2007. január 23. Információelmélet, kvantuminformatika
Petz Dénes: Neumann János és a kvantum bitek

2007. március 20.
Lovász László: Gumiszalagoktól algoritmusokig

2007. május 22.
Szász Domokos: A Brown mozgás matematikája

Friss információk a http://matek.fazekas.hu/portal/eloadas/ linken olvashatók. Az iskola címe: 1082, Budapest, Horváth Mihály tér 8.

Szász Domokos

A Brown mozgás matematikája

Játsszunk szabályos pénzérmével! Egy Ft-ot nyerünk, ha fejet dobunk, ugyanennyit vesztünk írás esetén. Felrajzolhatjuk a nyeremény időbeli alakulását, azaz az

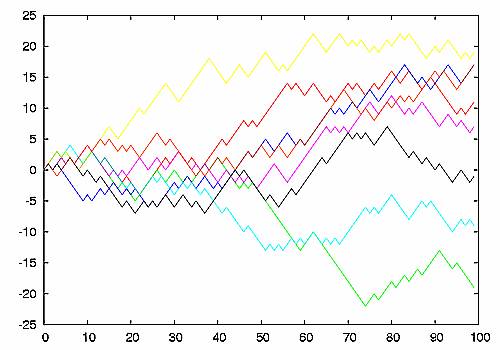
Az (n, S(n)) pontokat a síkba rajzolva és azokat szakaszokkal összekötve egyszerűnek kinéző, de igazából rendkívül gazdag viselkedésű véletlen függvényt kapunk. (Néhány realizáció látható az alábbi ábrán.) A modellt véletlen bolyongásnak nevezik és egy különlegesen érdekes történethez kapcsolódik.

Az ábra forrása: http://en.wikipedia.org/wiki/Random_walk

1827-ben Brown brit botanikus mikroszkópjával kőzetzárványba zárt folyadékot vizsgált, és azt találta, hogy abban a (nyilván élettelen!) apró részecskék kaotikus mozgást folytatnak. E rejtélyes mozgást Bachelier 1900-ban tőzsdei folyamatokkal azonosította, mígnem Einstein 1905-ben zseniális fizikai érveléssel azzal magyarázta, hogy az apró részecskéket még apróbbak - hőmozgásukból kifolyólag - folyamatosan taszigálják. 1920 és 1924 között Wiener matematikai modellt adott a Brown-mozgásra (érdekesség: a Wiener folyamat tipikus pályája sehol sem differenciálható függvény!).

Azóta is izgalmas kérdés, hogy milyen konkrét modellekben lesz egy megfigyelt részecske pályája a Wiener folyamat. Erdős és Kac 1946-ban a véletlen bolyongás megfelelően átskálázott változatára, tehát egy véletlen folyamatra igazolta a Wiener folyamathoz való konvergenciát. Máig izgalmas kutatási terület egyre reálisabb fizikai (és nemcsak vélet­lenül változó, hanem a mechanika törvényei által irányított, determinisztikus) modelleket is találni a Brown-mozgásra. E kérdésekbe vezet be az előadás.

Az atomoktól a csillagokig
Előadássorozat középiskolásoknak az ELTE Természettudományi Kar Fizikai Intézetében