Fizikából kitűzött gyakorlatok és feladatok
1997. szeptember

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat.

Mérési feladat

m. 190. Hány cm³ gáz fejlődik egyetlen pezsgőtabletta vízben való feloldása során?

XX. kerületi fizika-kémia verseny, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

FGy. 3079. Aki puszta kézzel akar diót törni, az általában két darabot fog egyszerre a markába. Miért könnyebb így feltörni a diót?

Öveges József emlékverseny, Tata

FGy. 3080. Egy nagyothalló ember házában az elektromos csengő működését egy izzólámpa világítása is jelzi. A csengőt a kerti kapunál és a bejárati ajtónál egyaránt lehet működtetni. Tervezz meg egy ilyen áramkört!

,,Keresd a megoldást!'' verseny, Szeged

FGy. 3081. Egy 100 méter széles folyó sebessége mindenütt 2 m/s. Az egyik partról elindul egy csónak, amely álló vízben 1 m/s állandó sebességgel képes haladni. Milyen messze van az a legközelebbi pont a túlsó parton, amelyet el tud érni?

Lánczos Kornél verseny, Székesfehérvár

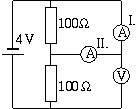
FGy. 3082. Az ábrán az I árammérő 10 mA áramot mutat, a voltmérő pedig 3 V feszültséget. Mit mutat a II. árammérő? Az árammérők egyformák, a telep belső ellenállása elhanyagolható.

Budó Ágoston verseny, Szeged

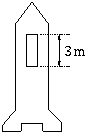
FGy. 3083. Egy űrrakéta kabinjának magassága 3 méter. A kabinban a levegő normál állapotban van. Mekkora a kabin padlózata és mennyezete közötti nyomáskülönbség:
a) indulás előtt, a kabin függőleges helyzetében?
b) indulás után, amikor a rakéta függőlegesen felfelé 40 m/s² gyorsulással emelkedik?
c) amikor az űrkabin a Föld körüli pályán kering?

Párkányi László verseny, Pécs

FF. 3084. Pontosan déli 12 órakor elindult egy bogár a toronyóra nagymutatójának forgástengelyétől, felfelé. Egyenletesen mászva a mutatón, negyedóra múlva ért a mutató végére. Mikor volt a legmagasabban?

Gidró Bonifác verseny, Révkomárom (Szlovákia)

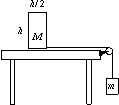
FF. 3085. Egy h magasságú, h/2 szélességű, M tömegű, homogén tömeg\-eloszlású hasábot vízszintes felületre helyezünk. A hasáb aljához egy fonalat erősítünk, melyet csigán vetünk át, és végére m tömegű testet akasztunk, majd a rendszert magára hagyjuk. A súrlódás mindenhol elhanyagolható. Mekkora m/M tömegaránynál billen meg a hasáb?

Nagy László verseny, Kazincbarcika

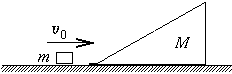
FF. 3086. Vízszintes talajon álló M tömegű lejtőre felcsúszik egy m tömegű, v₀ sebességű, kisméretű test. A súrlódás mindenhol elhanyagolható, a lejtő alja belesimul a vízszintes síkba. Mekkora maximális magasságig emelkedik fel a kis test a lejtőn?

Szilárd Leó verseny, Paks

FF. 3087. A lehulló nagy esőcseppek úgy növekednek, hogy esés közben befogják a velük ütköző kisebb cseppeket. Adj becslést arra, hogy mennyivel nő meg 10 másodperc alatt annak a 3 mm átmérőjű cseppnek a tömege, amelynek sebessége 5 m/s-ról egyenletesen 7 m/s-ra nő. Útja során a vizsgált csepp a levegőben lebegő 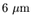sugarú cseppecskékkel találkozik. A kicsiny cseppek térbeli eloszlása egyenletes, köbcentiméterenkénti átlagos számuk kettőszáz.

Károly Ireneusz verseny, Kecskemét

FN. 3088. Egy bizonyos helikopter akkor tud lebegni, ha motorja P mechanikai teljesítményt ad le. Egy másik helikopter ennek pontosan 1/2-ére kicsinyített mása (minden lineáris mérete fele akkora). Mekkora P' mechanikai teljesítmény szükséges ahhoz, hogy ez a helikopter lebegjen?

Nemzetközi Fizikai Diákolimpia, Kanada

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1997. október 11.