Matematikából kitűzött gyakorlatok és feladatok
1997. november

Általános iskolások részére javasolt példák: C. 481., C. 482., C. 483., Gy. 3158., Gy. 3161.

A pontversenyben kitűzött C gyakorlatok

C. 481. Egy kör alakú asztalnál ülő társaság tagjai felállnak. Amikor visszaülnek, azt veszik észre, hogy mindenkinek mások a szomszédai, mint előzőleg. Hány tagú lehet a társaság?

Javasolta: Fried Ervin, Budapest

C. 482. Bizonyítsuk be, hogy ha az x, y valós számokra y³x+1<x+y³ teljesül, akkor x³y+1<y+x³.

C. 483. A Mindent vagy semmit! műveltségi vetélkedő egyik adásában hangzott el az a kérdés, hogy melyik az a síkidom, amelynek területe az átlók szorzatának a fele. ,,Deltoid'' - volt a hivatalos válasz. Vajon szükséges-e, hogy a keresett síkidom deltoid legyen?

C. 484. Adott egy egyenes körkúp 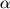félnyílásszöge. Hányadrésze a kúpba írható gömb térfogata a kúp térfogatának?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1997. december 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3158. Bizonyítsuk be, hogy ha a tízes számrendszerben felírt 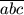szám osztható 7-tel, akkor a 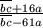tört egyszerűsíthető 7-tel.

Gy. 3159. Melyik az a legkisebb pozitív egész n, amelyre 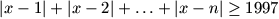teljesül minden x valós számra?

Gy. 3160. Van-e olyan különböző pozitív egészekből álló végtelen hosszú számtani sorozat, amelyben a jegyek összege is számtani sorozatot alkot?

Angol versenyfeladat

Gy. 3161. Egy összejövetelre n meghívott érkezett, közöttük Balogh úr. Rajtuk kívül ott van egy újságíró, aki Balogh úrral szeretne beszélni. Tudja, hogy Balogh urat senki sem ismeri, Balogh úr viszont mindenkit ismer. Az újságíró a meghívottak közül bárkihez odamehet, és bármelyik másikra rámutatva megkérdezheti tőle, ismeri-e.

a) Biztosan megtalálhatja-e Balogh urat n-nél kevesebb kérdéssel?

b) Hány kérdésre van szüksége, hogy megtalálja Balogh urat, ha szerencséje van?

Gy. 3162. Az a, b befogójú derékszögű háromszög átfogójának egyik végpontja köré a, a másik végpontja köré b sugarú kört rajzolunk. Bizonyítsuk be, hogy az átfogónak a két kör közös részébe eső szakasza ugyanolyan hosszú, mint a háromszögbe írt kör átmérője.

Gy. 3163. Legalább hány egyenest határoz meg a síkon n különböző, nem egy egyenesen fekvő pont?

Gy. 3164. Egy háromszög súlypontja S, magasságpontja M, beírt körének középpontja O, körülírt körének középpontja K. Ezen pontok közül valamely kettő egybeesik. Mely esetekben következik ebből, hogy a háromszög szabályos? (H)

Javasolta: Róka Sándor, Nyíregyháza

Gy. 3165. Hány olyan magasságvonala lehet egy tetraédernek, amelyik a tetraéderen kívül halad?

A pontversenyben kitűzött feladatok

F. 3196. Legyen az a_n sorozat a következő: a₀=1, a_n+1=sin a_n (n=0,1,2,...) Mutassuk meg, hogy az na_n² sorozat korlátos.

F. 3197. Egy 8x8-as sakktábla mezőin bábukat helyeztünk el úgy, hogy minden egyes sorban és oszlopban pontosan 4 bábu van. Bizonyítsuk be, hogy kiválasztható 8 bábu úgy, hogy közülük semelyik kettő nincs egy oszlopban vagy egy sorban.

F. 3198. Az a₁, a₁, ..., a_n számok különböző pozitív egészek. Bizonyítsuk be, hogy .

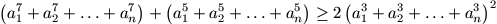F. 3199. Az ABC háromszög C-nél lévő szögét n egyenlő részre osztó egyenesek az AB oldalt a C₁, C₂, ..., C_n-1 pontokban metszik. Mutassuk meg, hogy az 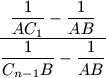tört értéke nem függ n-től.

F. 3200. Adottak az AB és a CD szakaszok. AB-t rögzítjük, CD-t pedig úgy mozgatjuk AB-vel párhuzamosan, hogy az ABCD négyszög mindig érintőtrapéz legyen. Milyen pályát ír le a mozgás során CD felezőpontja?

F. 3201. Legyen M az ABCD tetraéder egy tetszőleges belső pontja. Jelöljék rendre N, P, Q és A₁ a BCM, CDM, BDM, BCD síkoknak az AD, AB, AC, AM egyenesekkel való döféspontját. Végül messék az A-n átmenő, a BCD síkkal párhuzamos síkot az A₁N, A₁P és A₁Q egyenesek a D₁, B₁ és C₁ pontokban. Mutassuk meg, hogy a B₁C₁D₁ háromszög súlypontja A.

Javasolta: András Szilárd, Kolozsvár

A pontversenyben kitűzött nehezebb feladatok

N. 146. Igazoljuk, hogy a (0,1) intervallumba eső tetszőleges páratlan nevezőjű r racionális számhoz találhatók olyan x, y, z egészek, hogy az 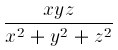törtrésze r-rel egyenlő.

N. 152. Adott a síkon véges sok, egységnyi sugarú körlemez, bármely kettő középpontjának távolsága legalább 10 egység. Igaz-e, hogy létezik olyan töröttvonal, amelynek csúcsai a körök középpontjai, minden középpont szerepel a töröttvonalon, és a vonalat alkotó szakaszoknak csak a végpontjaikat tartalmazó körökkel van közös pontja?

Javasolta: Pap Gyula, Debrecen

N. 153. Definiáljuk az 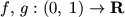függvényeket a következőképpen: , .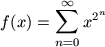

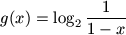a) Igazoljuk, hogy f-g korlátos.

b) Létezik-e az (f(x)-g(x)) függvénynek 1-ben bal oldali határértéke?

N. 154. Színezzük ki a sík pontjait két színnel a következőképpen: Ha [x]+[y] páros, akkor legyen az (x; y) pont fehér, ellenkező esetben pedig fekete. Tetszőleges a, b pozitív egészekre tekintsük azt a háromszöget, amelynek csúcsai a (0; 0), (0; a) és (b; 0) pontok, és legyen f(a,b) a fehér és fekete tartományok területe különbségének abszolút értéke. Mutassuk meg, hogy ha u_n a Fibonacci sorozat n-edik eleme (u₁=1, u₂=1, u_n+2=u_n+u_n+1), akkor .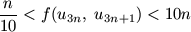

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1997. december 15.