Matematikából kitűzött gyakorlatok és feladatok
1998. november

Általános iskolások részére javasolt példák: C. 518., C. 519., Gy. 3230., Gy. 3234., Gy. 3237.

A pontversenyben kitűzött C gyakorlatok

C. 517. Átlagosan hányszor kell egy szabályos dobókockával dobni ahhoz, hogy a kapott számok összege legalább 3 legyen?

C. 518. Oldjuk meg a következő egyenletrendszert:

x²+yz=0,   v²+yz=0,   (x+v)y=2,   (x+v)z=-2.

C. 519. Egység sugarú körhöz szerkesszünk olyan négyzetet, amelynek két szomszédos csúcsa a körön van, a másik két csúcsot összekötő oldal pedig érinti a kört. Számítsuk ki a négyzet oldalait!

Fried Katalin (Budapest) javaslata alapján

C. 520. Térbeli derékszögű koordinátarendszerben egy origó középpontú gömb sugara 3 egység. Hány rácspont esik a gömb felületére?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. december 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3230. Van-e olyan természetes számokból álló a₁, a₂, ... sorozat, hogy tetszőleges k természetes számra az a₁+k, a₂+k, a₃+k, ... sorozat csak véges sok prímet tartalmaz?

Gy. 3231. Vannak-e olyan a, b, c egész számok, amelyekre az

ax²+bx+c=0   és az   (a+1)x²+(b+1)x+(c+1)=0

egyenletnek két-két egész gyöke van?

Orosz versenyfeladat

Gy. 3232. Hány olyan 100 jegyű természetes szám van, amelynek minden jegye páros és bármely két szomszédos jegyének a különbsége 2?

Gy. 3233. Bizonyítsuk be, hogy akárhogyan adunk meg 100 különböző pozitív egész számot, mindig kiválasztható közülük 98, amelyeknek az összege nem osztható a megmaradó kettő összegével. (H)

Gy. 3234. Vágjunk fel egy téglalapot 9 téglalapra úgy, hogy semelyik két téglalapot se lehessen összetenni egy újabb téglalappá.

Gy. 3235. Az AB és CD szakaszok egy síkban vannak. Szerkesszünk ebben a síkban olyan P pontot, amelyre az APB és CPD háromszögek hasonlóak, és P-nél levő szögük egyenlő.

Gy. 3236. Az ABC hegyesszögű háromszögben az A csúcsból húzott magasság talppontja T_a. Hasonlóan értelmezzük a T_b és T_c talppontokat. Bizonyítsuk be, hogy a T_aC+T_bA+T_cB szakaszok összege legalább akkora, mint a T_aT_bT_c háromszög kerülete. (H)

Árokszállási Tibor (Paks) javaslata alapján

Gy. 3237. Lehet-e egy kocka síkmetszete a) szabályos ötszög b) szabályos hatszög?

A pontversenyben kitűzött feladatok

F. 3250. Határozzuk meg azokat az f:(0, 1)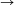R függvényeket, amelyekre:

f(x^.y)=x^.f(x)+y^.f(y).

F. 3251. Egy ping-pong versenyen bármely két versenyző pontosan egyszer játszott egymással. Egy A versenyző akkor kapott díjat, ha bármely másik B résztvevőt vagy legyőzött, vagy legyőzött valakit, aki B-t megverte. Mutassuk meg, hogy ha pontosan egy játékos kapott díjat, akkor ő mindenkit legyőzött.

Kínai versenyfeladat

F. 3252. Hányféleképpen lehet sorbarakni az 1, 2, ..., n számokat úgy, hogy az első helyen álló szám kivételével mindegyiket megelőzze legalább az egyik (eredeti sorrend szerinti) szomszédja?

F. 3253. Adott a k körvonal és rajta a P pont. Szerkesszük meg a k P-beli érintőjét egy darab egyélű vonalzó segítségével.

F. 3254. Egy transzformáció a sík P(x;y) pontjához 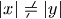esetén a pontjához 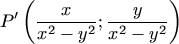pontot rendeli, |x|=|y| esetén pedig önmagát. Határozzuk meg a sík egyeneseinek a transzformációval kapott képét.

F. 3255. Egy egységsugarú gömbfelszín négy pontja köré egymást páronként nem metsző gömböket rajzoltunk. Mutassuk meg, hogy ha e gömbök sugarainak összege 2, akkor az egységgömb felszínének legalább a negyedét lefedik.

A pontversenyben kitűzött nehezebb feladatok

N. 187. Adottak egy gömb felszínén az egymástól és egymás átellenes pontjaitól különböző A, B, C és M pontok. Bizonyítsuk be, hogy ha az AM és BM főkörök merőlegesek a BC, illetve AC főkörökre, akkor a CM főkör is merőleges az AB főkörre.

N. 188. Egy fagráfot pⁿ típusúnak nevezünk, ha gyökerén kívül további n szintje van, és a legfelső szintjét kivéve minden csúcsban p-felé ágazik.

a) Egy 4ⁿ típusú gráf ,,leveleit'' (legfelső csúcsait) kiszíneztük 3k színnel. Mutassuk meg, hogy a gráf tartalmaz olyan 2ⁿ típusú részgráfot, amelynek levelei legfeljebb k színnel vannak színezve.

b) Tetszőleges k pozitív egészhez mutassunk példát olyan 4ⁿ típusú gráfra, amelynek levelei kiszínezhetők 3k+1 színnel úgy, hogy bármelyik 2ⁿ típusú részgráfjának levelein legalább k+1 szín szerepeljen.

Javasolta: Keleti Tamás, London

N. 189. Bizonyítsuk be, hogy tetszőleges a₁, ..., a_n pozitív egészekre

.

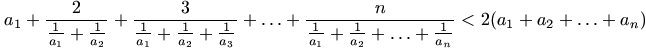N. 190. Bizonyítsuk be, hogy ha a p polinom foka legfeljebb 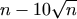, akkor

.

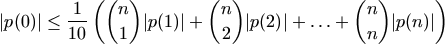A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1998. december 15.