Matematikából kitűzött gyakorlatok és feladatok
1999. április

Általános iskolásoknak javasolt feladatok: C.537, C.538, Gy. 3271, Gy. 3275, Gy. 3276.

A pontversenyben kitűzött C gyakorlatok

C. 537. Dolgozatírás közben Sanyi az órájára pillantva megállapította, hogy a dolgozatírás idejéből ötször annyi telt el, mint amennyi még hátra van. M perc múlva ez az arány már 8. Mennyi az arány újabb M perc elteltével?

C. 538. Milyen p (nem feltétlenül pozitív) prímek esetén lesz a 2p+1, 4p+1, 6p+1 kifejezések értéke is prím?

Javasolta: Kovács Ádám, Budapest

C. 539. Igazoljuk, hogy bármely hegyesszögű, egyenlő szárú háromszögben

AM=a/tg,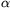

ahol szokásos módon a az alapot, A és 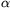az alappal szemközti csúcsot, illetve szöget, M pedig a magasságpontot jelöli.

C. 540. Vízszintes síkból kiemelkedik (az autósok bosszantására) egy 10 cm sugarú félgömb. A síkon gurul egy henger, amely palástjával a félgömbnek ütközik. Jelölje 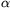a két test érintési pontjára illeszkedő közös érintősíknak a vízszintessel bezárt szögét. Legalább mekkora a henger sugara, ha 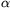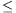30^o?

A C gyakorlatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. május 15.

A pontversenyben kitűzött gyakorlatok

Gy. 3270. Legyen n>2 páros szám. Igazoljuk, hogy 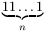semmilyen számrendszerben sem lehet prím.

Javasolta: Kovács Ádám, Budapest

Gy. 3271. Melyik tört a nagyobb, 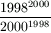vagy ?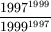

Javasolta: Bíró József, Budapest

Gy. 3272. Egy téglatest a, b, c élei egész számok, felszínének és térfogatának mérőszáma megegyezik. Mekkorák az élei, ha tudjuk, hogy ?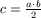

Javasolta: Kovács Ádám, Budapest

Gy. 3273. Mutassuk meg, hogy 5¹²+2¹⁰ összetett szám. (H)

Szentpétervári Matematikai Olimpia

Gy. 3274. Van három egybevágó, derékszögű háromszög alakú papírdarabunk. Ezek bármelyikét a magassága mentén kettévághatjuk. A kapott háromszögek közül valamelyiket ismét kettévághatjuk a magassága mentén, és így tovább. Mekkora lehet a befogók aránya, ha tudjuk, hogy az eljárás során mindig található két egybevágó háromszög?

Gy. 3275. Egy négyszög területét felezik az átlói. Igazoljuk, hogy együtt négy egyenlő területű részre bontják a négyszöget.

Gy. 3276. Az r sugarú k₁ kör kerületének egy O pontja a k₂ kör középpontja. A két kör metszéspontjai A és B, S pedig a k₁ belső pontja. A BS egyenes másik metszéspontja k₁-gyel T. Bizonyítsuk be, hogy ha az AOS háromszög szabályos, akkor TS=r. (H)

Gy. 3277. Adottak az a és b pozitív egész számok. Adjunk eljárást 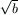megszerkesztésére, ha adott a 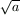hosszúságú szakasz.

Javasolta: Kovács Ádám, Budapest

A pontversenyben kitűzött feladatok

F. 3280. Bizonyítsuk be, hogy ha x₁, x₂, ..., x_n pozitív számok, akkor

.

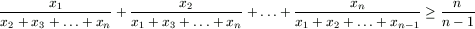F. 3281. Egy szelet csokoládét több lépésben osztunk részekre. Minden lépésben a már meglevő részek közül a legnagyobb tömegűt (ha több ilyen van, azok egyikét) osztjuk tovább úgy, hogy a kapott új darabok egyike se legyen nagyobb tömegű, mint a most tovább osztott rész fele. Igazoljuk, hogy a k-adik lépés után kapott részek mindegyike kisebb, mint az eredeti csokoládé tömegének a 2/(k+1)-edrésze.

Lovász László, Budapest

F. 3282. Milyen határok között változik x²+2xy, ha x²+y²=1?

F. 3283. Adott 2000 darab szakasz, mindegyik hossza legalább 1 egység. Akárhogyan választunk ki közülük néhányat, azokból nem szerkeszthető sokszög. Mutassuk meg, hogy a szakaszok összhossza legalább 2¹⁹⁹⁹.

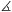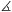F. 3284. Az ABC háromszög belsejében levő P pontra PAB=PBC=PCA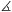=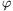. Mutassuk meg, hogy ha a háromszög szögei 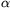, 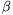és 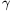, akkor

.

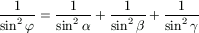F. 3285. Adott a síkon egy k körvonal és rajta kívül egy P pont. Hol helyezkednek el azon körök középpontjai, amelyek egy k-t tartalmazó gömb és egy P csúcsú egyenes körkúp érintési pontjaiként állnak elő?

A pontversenyben kitűzött nehezebb feladatok

N. 207. Az f:[0, 1]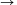[0, 1] folytonos függvényről tudjuk, hogy tetszőleges x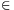[0, 1] valós számra az f(x), f(f(x)), f(f(f(x))), ... sorozat tartalmazza a 0-t. Következik-e ebből, hogy elég nagy n esetén 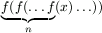azonosan 0?

N. 208. Bizonyítsuk be, hogy ha p 2-nél nagyobb prímszám, akkor létezik p-nél kisebb q prím, amelyre q^p-1-1 nem osztható p²-tel.

N. 209. Adjunk meg a síkon 6 olyan pontot, amelyek közül bármelyik kettő távolsága egész, semelyik három nincs egy egyenesen, és semelyik négy nincs egy körön.

N. 210. Mutassuk meg, hogy bármely zárt térgörbének van négy olyan pontja, amelyek egy síkban vannak. Igaz-e ez az állítás öt pontra is?

Javasolta: Róka Sándor, Nyíregyháza

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. május 15.