Fizikából kitűzött gyakorlatok és feladatok 1999. október

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 209. Állítsunk fel dominókat egymással párhuzamosan, egymástól egyenlő távolságra úgy, hogy az elsőt meglökve az egész sor ledőljön. Vizsgáljuk meg, mitől és hogyan függ a dőlési hullám sebessége! (6 pont)

Közli: Bakonyi Gábor, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3274. A tengerparton álló, 26 méter magas világítótorony tetején lévő reflektor fényét egy hajó távcsövén át 30 km-ről látták meg először . Milyen magasan volt a távcső a tenger szintje felett? (4 pont)

Közli: Radnai Gyula, Budapest

P. 3275. Milyen mélyre kell lenyomni egy úszó fahasábot a vízben, hogy az eközben végzett munka megegyezzék a hasáb vízből történő kiemeléséhez minimálisan szükséges munkával? A fa sűrűsége a víz sűrűségének k-ad része. Vizsgáljuk meg a k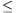2 esetet külön is! (4 pont)

Öveges József fizikaverseny országos döntője, Tata

P. 3276. Adjunk becslést az egyetemes gázállandóra a 100 ^oC-os vízgőzre vonatkozó alábbi mérési adatok felhasználásával:

p (Pa)	986	9806	98066
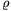(kg/m3)	0,00570	0,05705	0,578

Közli: Bakonyi Gábor, Budapest

P. 3277. Tarzan egy szikla széléről elrugaszkodva 18 m hosszú indán lendül egy másik sziklaszirt felé. A szikla tetejéről a pálya legmélyebb pontjáig 3 métert süllyed. Kibírja-e az inda a 900 N súlyú Tarzan ugrását, ha a szakítószilárdsága 1200 N? (4 pont)

Budó Ágoston verseny, Szeged

P. 3278. Két különböző nagyságú, de azonos maximális teljesítményű ellenállást sorosan vagy párhuzamosan kell kapcsolni ahhoz, hogy minél nagyobb teljesítményű lehessen a kettő együtt? (4 pont)

Közli: Gulyás János, Budapest

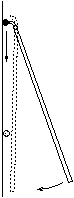P. 3279. A nehézségi gyorsulás mérésére használt egyik eszköz az ábrán látható ún. Whiting-féle deszkás inga. Igazoljuk, hogy a deszka forgástengelyétől a deszkával egyszerre indított, szabadon eső golyó becsapódása a deszka hosszának mindig ugyanannyiad részénél történik, függetlenül a deszka hosszától! Mekkora ez az arány? (4 pont)

Közli: Nagy Tibor, Szolnok

P. 3280. Csökkentsük vagy növeljük a vízgőzzel telített levegő térfogatát azért, hogy a vízgőz egy része kicsapódjék a levegőből? (4 pont)

Közli: Fári Jánosné, Szigetvár

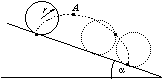P. 3281. Határozzuk meg a lejtőn csúszás nélkül legördülő karika egy pontja által leírt pálya legfelső A pontjában a görbületi sugarat! (5 pont)

Orosz feladat nyomán

P. 3282. Egy R sugarú, kör alakú vezetőt Q töltéssel elektromosan feltöltöttünk. Hogyan változik a térerősség a kör középpontján átmenő, a kör síkjára merőleges egyenes mentén? Hol éri el a legnagyobb értékét? (5 pont)

Bródy Imre verseny, Ajka

P. 3283. Egy gépkocsi mindegyik kerekének ugyanolyan erős felfüggesztő rugója van. Mennyit emelkedik meg a gépkocsi merevnek tekinthető karosszériája a kerekek felett, ha a gépkocsi a a jobb első kerekével egy 8 cm magas járdaszegélyre áll? Hogyan módosul az eredmény, ha a gépkocsi mindkét jobb oldali kerekével felhajt a járdára? Függ-e az eredmény attól, hogy hányan és hogyan ülnek a kocsiban? (6 pont)

Közli: Gnädig András, Budapest (Olimpiai válogatóverseny, 1999.)

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 1999. november 11.