Matematikából kitűzött gyakorlatok és feladatok
1999. október
Figyelem! A pontverseny feltételei a tavalyi évhez képest megváltoztak. Kérjük, olvassa el a versenykiírást!
 |
A C pontversenyben kitűzött (könnyebb) gyakorlatok |
C. 550. Egy horgász a napi zsákmánya össztömegének 35%-át kitevő három legnagyobb halat a mélyhűtőbe tette. A három legkisebb halat, amelyek együttesen a megmaradt rész 5/13-át tették ki, elvitte a macska, a többit pedig megfőzték ebédre. Hány halat fogott a horgász?
Javasolta: Dobos Sándor, Budapest
C. 551. Határozzuk meg az x2+y2=x, 2xy=y egyenletrendszer összes megoldását.
Javasolta: Fried Ervin, Budapest
C. 552. Az ábrán látható két kör középpontja 5 cm-re van egymástól, sugaraik hossza 3 cm és 4 cm. Mekkora a két satírozott terület különbsége?
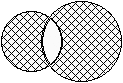
C. 553. Egy 20 cm magas, 10 cm átmérőjű henger "meghízott". Magassága és alapjai nem változtak, alkotója viszont 1 mm-rel megnyúlt, és így két egybevágó csonkakúppá formálódott. Hány százalékkal nőtt a henger térfogata?
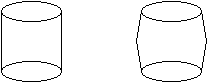
C. 554. Mutassuk meg, hogy van olyan a szám, hogy log2x+log3x=logax teljesül minden pozitív x-re.
 |
A B pontversenyben kitűzött feladatok |
B. 3302. Egy jegypénztárnál nyolcan állnak sorba. Négyüknél egy-egy 100 Ft-os, a másik négynél egy-egy 200 Ft-os van, sorrendjük véletlenszerű. A jegy ára 100 Ft, a kassza kezdetben üres. Mindenki egy jegyet szeretne vásárolni. A lehetséges sorrendek hányadrésze olyan, hogy a pénztáros fennakadás nélkül ki tudja adni a jegyeket? (3 pont)
B. 3303. Egy 5 cm széles papírcsíkot gyűrődés nélkül áthajtunk az ábra szerint.
Milyen kicsi lehet a kétszer lefedett, satírozott rész területe? (4 pont)
B. 3304. Meg lehet-e számozni egy kocka éleit az 1, 2, 3,..., 11, 12 számokkal úgy, hogy mindegyik csúcsban ugyanannyi legyen az ide befutó élekre írt számok összege? (4 pont)
Javasolta: Reményi Gusztáv, Budapest
B. 3305. Sándor Mátyás esetéből okulva, a hazafiak vezére egy egyenletet küldött barátainak:
2x2+4xy+7y2-12x-2y+N=0.
A titkos üzenet az volt, hogy a hónap N. napján legyen a felkelés. A hazafiak gyakran mondogatták, hogy a felkelés az egyetlen megoldás. Ez jellemzte N-et is: az egyenletet egyetlen (x,y) valós számpár elégítette ki. Mennyi N értéke? (4 pont)
B. 3306. Az egységnyi területű ABC háromszög AB oldalán a harmadolópontok legyenek D és E, az AC oldalán a felezőpont pedig F. A CB egyenesét az FE egyenes G-ben, az FD egyenes H- ban metszi. Határozzuk meg az FGH háromszög területét. (3 pont)
B. 3307. Határozzuk meg az ábrán látható MAN, MBN, MCN, MDN, MEN szögek összegét, ha tudjuk, hogy PA=AB=BC=CD=DE. (3 pont)
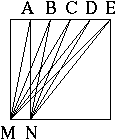
Orosz versenyfeladat
B. 3308. Hány olyan ikerprím számpár van, amelyek összege prímhatvány? (Ikerprímnek nevezünk két prímszámot, ha a különbségük 2.) (4 pont)
Javasolta: Kovács Ádám, Budapest
B. 3309. Egy kocka minden lapján kijelöltük a középvonalak negyedelőpontjait. Hogyan aránylik a pontok által meghatározott test térfogata a kocka térfogatához? (4 pont)
B. 3310. Mutassuk meg, hogy az (x2+y2)3=27x2y2 egyenletű görbe belefoglalható egy 4 egység oldalú négyzetbe. (5 pont)
B. 3311. Igazoljuk, hogy ha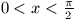 
, akkor
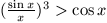
(5 pont).
Kovács Ádám (Budapest) ötletéből
 |
A pontversenyben kitűzött nehezebb feladatok |
A. 218. Határozzuk meg azokat a folytonos
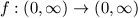függvényeket, amelyekre tetszőleges x, y pozitív számok
esetén
.
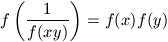A. 219. A H ponthalmaz a sík 2n pontját tartalmazza, közülük semelyik három nem esik egy egyenesre. Ha P és Q két különböző H-beli pont, és H-nak pontosan ugyanannyi pontja esik a PQ egyenes két oldalára, akkor a PQ szakaszt felező szakasznak hívjuk. Bizonyítsuk be, hogy ha a felező szakaszok száma n, akkor közülük bármelyik kettő metszi egymást.
Javasolta: Solymosi József, Budapest
A. 220. Jelöljük tetszőleges pozitív egész n számra S(n)-nel az n jegyeinek összegét tízes számrendszerben. Igazoljuk, hogy
.
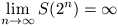A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
Bolyai János Matematikai Társulat (KöMaL feladatok); Budapest, Pf. 433. 1371
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)