Fizikából kitűzött gyakorlatok és feladatok 1999. december

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 211. Egy rosszul elzárt vízcsapból lecseppenő cseppek látszólag egyenlő időközönként követik egymást. Figyeljük meg hosszabb időn keresztül ezt a jelenséget! Milyen módon jellemezhetjük az időközök különbözőségét? (6 pont)

Közli: Rajkovits Zsuzsa, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

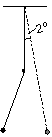P. 3295. Egy fonálinga lengés közben egy szögbe ütközik, amikor áthalad a függőleges egyensúlyi helyzeten. A szög éppen a fonál felénél helyezkedik el. Hány százalékkal rövidebb idő alatt tér vissza ilyenkor az inga az eredeti, 2^o-kal kitérített helyzetébe, mint ha nem lenne ott a szög? (3 pont)

Közli: Bordy Csongor, Bonyhád, Petőfi S. Evangélikus Gimn.

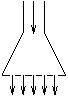P. 3295. Egy zuhanyrózsán 18 kör alakú, 2 mm átmérőjű lyuk van. A zuhanyrózsához vezető, 10 mm átmérőjű csövön 0,5 m/s sebességgel áramlik a víz. Mekkora sebességgel jön ki a víz a lyukakon? Változik-e a víz mozgási energiája? Nő vagy csökken? Adjunk magyarázatot! (4 pont)

Angol feladat nyomán

P. 3296. Van N darab különféle rugónk. Ha ezeket sorba kapcsoljuk, 52 N/m direkciós erejű rugót kapunk. Ha párhuzamosan kapcsoljuk a rugókat, akkor az eredő direkciós erő 1872 N/m lesz. Legfeljebb mekkora lehet N értéke? (4 pont)

Közli: Münz Márton, Budapest, Alternatív Közgazdasági Gimn.

P. 3297. Más gravitációs hatástól mentes környezetben két 1 kg-os ólomgolyó indul el egymás felé a tömegvonzás következtében. Mennyi idő múlva ütköznek össze, ha elinduláskor a golyók középpontjainak távolsága 1 méter volt? (Az ólom sűrűsége 11 340 kg/m³.) (4 pont)

Közli: Kóbor János, Miskolc

P. 3298. Kezdetben 7 liter térfogatú, 10⁵ Pa nyomású, 0 ^oC-os levegővel egy hőerőgépben olyan körfolyamatot végeztetünk, amely két izobár és két izochor szakaszból áll. A körfolyamat során a levegő sohasem hidegebb 0 ^oC-nál, és a gép által végzett munka 500 J. Legfeljebb mekkora lehet ennek a gépnek a termodinamikai hatásfoka? (5 pont)

Közli: Varga István, Békéscsaba

P. 3299. Egy síkkondenzátor egyik lemeze Q töltésű, másik lemeze töltetlen. A lemezek távolsága d, területe A.

a) Mekkora a kondenzátor feszültsége?

b) Mekkora és milyen irányú erő hat a 2. fémlemezre, ha az ábra szerint egy vezetékkel összekapcsoljuk a vele párhuzamos, azonos területű 3. fémlemezzel? (4 pont)

Közli: Kotek László, Pécs

P. 3300. Növelhetjük-e az akkumulátor által táplált fogyasztón (pl. egy autó indítómotorján) átfolyó áramot úgy, hogy az akkumulátorral párhuzamosan kapcsolunk egy vele megegyező elektromotoros erejű galvánelemet? (3 pont)

Közli: Radnai Gyula, Budapest

P. 3301. Egyrétegű szolenoid tekercset készítünk adott d átmérőjű, 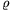fajlagos ellenállású fémhuzalból úgy, hogy egy r sugarú papírhengerre tekerjük, egymáshoz szorosan illeszkedő (szigetelt) menetekkel. A kész tekercset R belső ellenállású áramforráshoz kapcsoljuk. Hány menetesre készítsük a tekercset, hogy a mágneses tér által raktározott energia maximális legyen? (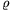=1,78^.10^-8  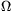m; R=1,2 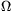; d= mm; r=3 cm.) (5 pont)

Közli: Légrádi Imre, Sopron

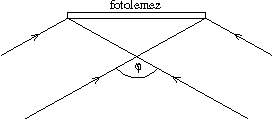P. 3302. Holografikus rácsot úgy készítenek, hogy egy párhuzamos lézernyalábot két egyenlő intenzitású nyalábra osztanak, majd 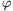szögben interferenciát hoznak létre egy fényérzékeny lemez felületén.

Mekkora szögben találkozott a két nyaláb, ha az így elkészült optikai rácsot merőlegesen megvilágítva éppen megfigyelhetjük másodrendben a teljes látható színképet? A rács előállításához 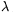₀=632 nm-es He--Ne lézert használtak. (A látható színképtartomány 380 nm-től 760 nm-ig terejed.) (5 pont)

Budó Ágoston verseny, Szeged

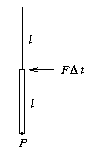P. 3303. Egy m tömegű, l hosszúságú homogén rúd az ábrán látható módon van felfüggesztve egy l hosszú fonálra. A rúd felső végét egy kicsiny Ft erőlökés éri. Írjuk le a rúd legalsó P pontjának mozgását! (6 pont)

Közli: Balogh Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. január 11.