Matematikából kitűzött gyakorlatok és feladatok
2000. február

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 570. Határozzuk meg azokat a háromjegyű prímszámokat, amelyekben a számjegyek szorzata 189.

C. 571. Egy kertben álló négyzet alapú kutyaház oldala 1,2 m hosszú. Az egyik sarkától 30 cm-re, a bejáratával azonos oldalon a kutyaház külső falához kötötték ki a kutyát egy 3 méteres lánccal. Mekkora területen mozoghat a kutya?

C. 572. A 6 cm sugarú körbe írt szabályos hatszög és beírt négyzet egy-egy oldala párhuzamos. Számítsuk ki a kör azon részének területét, amely a hatszög és a négyzet párhuzamos oldala között van és nem tartalmazza a kör középpontját.

C. 573. Határozzuk meg mindazokat az n pozitív egész számokat, amelyekre

1²+2²+...+n²=1+2+...+(2n-1)+2n.

C. 574. Milyen összefüggésnek kell fennállnia egy téglatest élei között ahhoz, hogy kettévágható legyen két egybevágó, az eredetihez hasonló téglatestre?

A B pontversenyben kitűzött feladatok

B. 3342. Határozzuk meg azokat a pozitív egész számokat, amelyekre n²-19n-99 négyzetszám. (3 pont)

Amerikai feladat

B. 3343. Az ABC háromszög AB oldalának felezőpontja F. Az AFC háromszög súlypontja S₁, a BFC háromszög súlypontja S₂. Az AS₁ egyenes a BC oldalt a P₁ pontban, a BS₂ egyenes az AC oldalt a P₂ pontban metszi. Igazoljuk, hogy az S₁S₂P₁P₂ négyszög paralelogramma. (3 pont)

B. 3344. Tekintsük azokat a természetes számokat, amelyek osztóinak számát megkapjuk úgy, hogy a prímtényezős felbontásukban szereplő prímszámok szorzatából kivonjuk a hatványkitevők szorzatát. Ilyen például a 25 és a 600 is. Bizonyítsuk be, hogy végtelen sok ilyen szám van. (4 pont)

B. 3345. Egy egyfordulós, körmérkőzéses focibajnokságon 9 csapat indult. Az Alsórákosi STC csapata 5 győzelmet aratott és 3 vereséget szenvedett. Lehetséges-e, hogy ezek után a csapat csak 7. lett? (A győzelemért 3, a döntetlenért 1-1 pont jár, azonos pontszám esetén a sorrendet a gólkülönbség dönti el.) (4 pont)

B. 3346. Száz darab súlyt, melyek egyenként rendre 1, 2, ..., 100 gramm tömegűek, úgy helyeztünk el egy kétkarú mérleg két serpenyőjébe, hogy a mérleg egyensúlyban van. Bizonyítsuk be, hogy a serpenyőkből elvehetünk két-két súlyt úgy, hogy a mérleg továbbra is egyensúlyban maradjon. (5 pont)

Tournament of Towns, 1999.

B. 3347.  Tekintsünk egy négyszöget     (a) a csúcsaiból álló pontnégyesnek;(b) homogén lemeznek. Milyen négyszögek esetén esik egybe a kétféle alakzat súlypontja? (4 pont)

Javasolta: Bogdán Zoltán, Cegléd

B. 3348. Határozzuk meg az 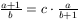egyenlet egész megoldásait. (4 pont)

Javasolta: Fried Ervin, Budapest

B. 3349. Mutassuk meg, hogy a p^p=q^q egyenletnek végtelen sok olyan pozitív racionális megoldása létezik, ahol p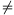q. (5 pont)

Javasolta: Lóczi Lajos, Budapest

B. 3350. Adott egy téglatest és a belsejében egy P pont. Tükrözzük P-t a téglatest minden lapjára. A hat tükörkép által meghatározott konvex test térfogata a P pont mely helyzetében lesz a legnagyobb? (3 pont)

B. 3351. Adott a térben legalább négy körvonal úgy, hogy középpontjaik közül semelyik 4 nincs egy síkban. Igaz-e, hogy ha bármely két körvonalhoz létezik őket tartalmazó gömbfelület, akkor létezik olyan gömbfelület is, amelyik mindegyik körvonalat tartalmazza? (5 pont)

A pontversenyben kitűzött nehezebb feladatok

A. 230. Határozzuk meg azokat az a egész számokat, amelyekre

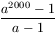
négyzetszám.

A. 231. Bizonyítsuk be, hogy ha egy összefüggő egyszerű gráfban minden csúcs foka legalább 3, akkor tartalmaz olyan kört, amelynek éleit elhagyva a gráf összefüggő marad.

Javasolta: Kiss Tamás, Budapest

A. 232. Mutassunk példát olyan konvex poliéderre, amelynek legalább 2000 csúcsa van, nincs 1/2-nél rövidebb éle, ugyanakkor belefér egy egységnyi sugarú gömbbe.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. március 16.