Fizikából kitűzött gyakorlatok és feladatok 2000. május

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 216.  ,,Miképp fejthetni meg azt, hogy a delejes acélrúd hatása a rúd közepe táján semmi, a rúd végei felé pedig mindinkább növekszik? - kérdezte Jedlik Ányos egy vizsgán 1871-ben.

Mérjük meg egy iskolai rúdmágnes környezetében a B mágneses indukció irányát, és szemléltessük a mágneses mezőt B-vonalakkal. (6 pont)

Közli: Radnai Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3344. A kerékpárdinamó vízszintes forgó tárcsája az R sugarú kerék tengelyétől r távolságra, pontosan a tengely fölött ér hozzá a kerékhez. A tárcsa és a kerék csúszás nélkül gördülnek egymáson, s a kerék is csúszás nélkül gördül a talajon. Mekkora sebességgel halad előre a tárcsának az érintkezéssel átellenes pontja, ha a kerékpár v sebességgel halad? (5 pont)

Lánczos Kornél verseny, Székesfehérvár

P. 3345. Egy 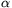=30^o-os hajlásszögű lejtőn lévő, m=6 kg tömegű, r=0,1 m sugarú tömör hengert a palástjához rögzített fonál segítségével tartunk egyensúlyban. A henger a lejtőn nem csúszik meg.

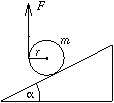
a) Mekkora F erővel tudjuk egyensúlyban tartani a hengert, ha a fonalat függőlegesen tartjuk?

b) Milyen irányban kell húzni a fonalat, hogy a lehető legkisebb erővel tarthassuk a hengert? Mekkora ez az erő?

c) Legalább mekkorának kell lennie a súrlódási együtthatónak az a), illetve b) esetben? (5 pont)

Közli: Kotek László, Pécs

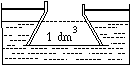P. 3346. Egy csonkakúp-palást alakú, lefelé szélesedő edény fenéklapjához elhanyagolható súlyú, jól illeszkedő korongot szorítunk, majd az edényt az ábrán látható víztartályba merítjük, és a palástjánál fogva a tartályhoz rögzítjük. A kiszorított víz térfogata 1 dm³. Ezután a korongra egy 1 kg-nál kicsit nagyobb tömegű jégdarabot helyezünk. Mi történik, ha a jég elolvad? (Az olvadó jég nem ér hozzá az edény oldalához.) (5 pont)

Közli: Gálfi László, Budapest

P. 3347. Legalább hányszorosa legyen a fonálinga végén lévő, pontszerűnek tekinthető test tömege a fonál tömegének, hogy az inga lengésideje legfeljebb 1 %-kal térjen csak el a matematikai inga lengésidejétől? (4 pont)

Közli: Simon Péter, Pécs

P. 3348. Az ábrán látható hosszú, vízszintes sínpárt R ellenállással hidaljuk át. A sínek távolsága l, elektromos ellenállásuk elhanyagolható. A sínpáron súrlódás nélkül csúszhat egy m tömegű, l hosszúságú vezető rúd, függőleges, B indukciójú homogén mágneses térben.

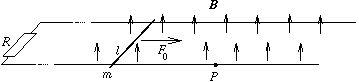
A vezető rúdra már hosszú ideje F₀ nagyságú erőt fejtünk ki, melynek hatására állandósult sebességgel csúszik. Egy bizonyos P pontnál a külső erőhatást megszüntetjük. Mekkora utat tesz meg a vezető rúd a P ponttól a megállásig? (5 pont)

Varga István, Békéscsaba feladata alapján

P. 3349. Egymástól jó távol helyezkedik el két egyforma szupravezető gyűrű. Az egyik (A) gyűrűben I₀ erősségű áram folyik, a másikban (B) nem folyik áram. A két gyűrűt lassan közelítjük egymáshoz. Mekkora áram fog folyni A-ban, amikor a másik gyűrűben I₁ erősségű áram folyik? (Egy szupravezető gyűrű által körülfogott mágneses fluxus értéke nem változhat meg.) (5 pont)

Közli: Bodor András, Budapest

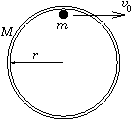P. 3350. Vízszintes asztallapon fekvő M tömegű, r sugarú vékony, keskeny abroncs belsejében, az abroncshoz érintkezve áll egy m tömegű kis test. Hogyan fog mozogni az abroncs középpontja, ha a kis testet érintő irányú, v₀ nagyságú kezdősebességgel elindítjuk? Mennyi idő múlva és hol lesz újra zérus az abroncs sebessége? (A súrlódás mindenütt elhanyagolható.) (5 pont)

Közli: Gnäadig Péter, Budapest

P. 3351. v₀ sebességgel, súrlódás nélkül mozgó m tömegű pontszerű test rugalmasan ütközik a k rugóállandójú rugóval összekapcsolt két, egyenként M tömegű, pontszerű testből álló R rendszerrel.

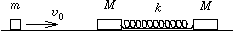
a) Legalább mekkora legyen a m/M arány, hogy egy második ütközés is létrejöjjön az m tömegű test és az R rendszer között?

b) Legfeljebb mennyi idő telik el a két ütközés között? (6 pont)

Francia felvételi feladat (École Normale Superieure, Párizs)

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. június 11.