A 2000 szeptemberi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 242. Egy 5x5x10-es téglatestben adott 2001 pont. Bizonyítsuk be, hogy ki tudunk közülük választani kettőt, amelyek távolsága kisebb, mint 0,7.

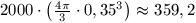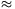Megoldásvázlat. Rajzoljunk mindegyik pont köré egy 0,35 sugarú gömböt. Ezek térfogatának összege . Ha a téglatest lapsíkjait 0,35 egységgel kijjebb toljuk, akkor ez tartalmazza az összes gömböt. A kibővített téglatest térfogata 5,7^.5,7^.10,7347,6, ami kisebb a gömbök térfogatának összegénél. Ezért a gömbök nem lehetnek diszjunktak. Ha viszont valamelyik két gömb egymásba lóg, akkor ezek középpontjainak távolsága kisebb, mint 0,7.

A. 243. Határozzuk meg mindazokat a p és q prímszámokat, amelyekre alkalmas n>1 esetén

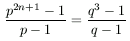Javasolta: Fried Ervin, Budapest

Megoldásvázlat. A jobboldalon egyszerűsítve, mindkét oldalból 1-et kivonva majd beszorozva

p(pⁿ-1)(pⁿ+1)=(p-1)q(q+1).

Ha q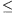pⁿ-1 lenne, akkor a baloldal tényezőnként nagyobb lenne a jobboldalnál, ami ellentmondás. Tehát q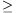pⁿ; mivel azonban q prím, pⁿ pedig összetett, ebből következik, hogy q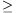pⁿ+1.

Mivel q prím, a baloldalon valamelyik tényező osztható q-val. Az előbiek alapján ez csak úgy lehetséges, ha q=pⁿ+1. Ezt behelyettesítve kapjuk, hogy

p(pⁿ-1)=(p-1)(pⁿ+2), azaz pⁿ-3p+2=0.

Ebből p|2, p=2, n=2, végül q=pⁿ+1=5.

A. 244. Egy számsorozatot nevezzünk Fibonacci-típusúnak, ha a harmadiktól kezdve mindegyik eleme az előző kettő összege. Bizonyítsuk be, hogy a pozitív egész számok halmaza felbontható olyan Fibonacci-típusú végtelen sorozatok uniójára, amelyek közül semelyik kettőnek nincs közös eleme.

Javasolta: Énekes Béla, Tolna

1. megoldás. Definiálunk egy f: N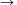N függvényt. Ez a függvény minden számhoz az illető számot tartalmazó sorozat következő elemét fogja rendelni.

Legyen f(1)=2. Ha f(1), ..., f(n-1) már definiálva van, akkor vizsgáljuk meg, hogy az n szám előáll-e függvényértékként. Ha n=f(m) valamilyen m-re, akkor vegyük a legkisebb ilyet, és legyen f(n)=n+m. Ha az n nem áll elő függvényértékként, akkor pedig legyen f(n)=f(n-1)+1. Az első néhány érték:

f(1)=2
f(2)=2+1=3	mert 2=f(1)
f(3)=3+2=5	mert 3=f(2)
f(4)=5+1=6
f(5)=5+3=8	mert 5=f(3)
f(6)=6+4=10	mert 6=f(4)
f(7)=10+1=11
f(8)=8+5=13	mert 8=f(5)
f(9)=13+1=14
f(10)=10+6=16	mert 10=f(6)
f(11)=11+7=18	mert 11=f(7)
...

Minden olyan n számra, ami nem áll elő f értékeként, vegyük az n, f(n), f(f(n)), ... sorozatot. Ez Fibonacci-típusú, mert f definíciója szerint f(f(x))=f(x)+x tetszőleges x-re:

1235813...

4610162642...

71118294776...

914233760...

...

A konstrukció miatt minden pozitív egész szerepel legalább egy sorozatban. Ha még azt is bebizonyítjuk, hogy f szigorúan monoton, akkor azt is garantáljuk, hogy a sorozatoknak nincs közös eleme.

I. lemma. Minden n-re f(n)>n. Ez indukcióval azonnal kijön. Ha n=f(m), akkor f(n)=n+m>n. Ha n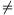f(m), akkor f(n)=f(n-1)+1>(n-1)+1=n.

II. lemma. Az f függvény szigorúan monoton nő. Szintén indukció; n<10-re már láttuk. Ha n nem áll elő f(m) alakban, akkor f(n)=f(n-1)+1>f(n-1). Ha n=f(m), akkor az I. lemma miatt csak m<n lehetséges, és az indukciós feltevés szerint csak egy ilyen m létezik. Legyen k=f(m-1). Erre persze k<n. A k+1, k+2, ..., n-1 számok az f(m-1)=k és f(m)=n függvényértékek közé esnek, ezért nem értékei f-nek. Ezért

f(k)=k+(m-1)	mert k=f(m-1),
f(k+1)=f(k)+1=k+m,
f(k+2)=f(k+1)+1=k+m+1,
...
f(n-1)=f(n-2)+1=n+m-2.
f(n)=n+m,	mert n=f(m).

Ebben az esetben is f(n)>f(n-1). Az f függvény tehát szigorúan monoton nő.

2. megoldás. Az előző megoldáshoz hasonlóan ismét egy olyan f: N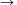N függvényt definiálunk, amely szigorúan monoton nő és teljesül rá az f(f(n))=f(n)+n függvényegyenlet.

Legyen 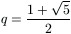a q²=q+1 egyenlet pozitív gyöke, és legyen tetszőleges n pozitív egészre f(n) a qn-hez legközelebbi egész szám. Erre a föggvényre is teljesül, hogy f(n)>n, mert qn)>n+.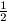

A szigorú monotonitás is igaz, mert qn és q(n+1) különbsége nagyobb, mint 1, így a q(n+1)-hez legközelebbi egész nagyobb, mint a qn-hez legközelebbi egész.

Végül tetszőleges n pozitív egészre

|f(f(n))-f(n)-n|=|f(f(n))-qf(n)+(q-1)f(n)-q(q-1)n|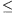

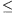|f(f(n))-qf(n)|+(q-1)|f(n)-qn|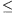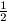+(q-1)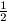^.<1, amiből f(f(n))-f(n)-n=0.

3. megoldás. Ismeretes, hogy minden pozitív egészt egyértelműen fel lehet írni olyan Fibonacci-számok összegeként, amelyek mind különbözők, és szomszédosak sincsenek közöttük, például 17=1+3+13. Tekintsünk egy tetszőleges pozitív egészt, amelynek felírásában az 1 szerepel. Ha ebbenn az összes tagot kicseréljük a rákövetkező Fibonacci számra, akkor egy újabb számot kapunk, illetve ezt a felírást ismételgetve pedig egy Fibonacci típusú sorozatot:

1+3+132+5+213+8+345+13+55...

Ha ezt minden lehetséges kezdőelemre megtesszük, végtelen sok Fibonacci-típusú sorozatot kapunk. Minden pozitív egész n-et pontosan az egyik sorozat tartalmaz, mert az n felírását visszacsúsztatva egyértelműen meghatározható az n-et tartalmazó sorozat kezdőeleme; például a 100=3+8+89 számot az 1+2+34=37 kezdőelemű sorozat tartalmazza.

1, 2, 3, 5, 8, 13, 21, ...

4=1+3, 7=2+5, 11=3+8, 18=5+13, 29=8+21, ...

6=1+5, 10=2+8, 16=3+13, 26=5+21, 42=8+34, ...

9=1+8, 15=2+13, 24=3+21, 39=5+34, 63=8+55, ...

12=1+3+8, 20=2+5+13, 32=3+8+21, 52=5+13+34, ...

...

Zsbán Ambrus és Csíkvári Péter dolgozata alapján

Megjegyzés. A cikkel kapcsolatban rövidesen cikk is megjelenik a KöMaL-ban.

Már regisztráltál?
Új vendég vagy?