Fizikából kitűzött gyakorlatok és feladatok 2000. október

Beküldhető a mérési feladat és legfeljebb 5 (szabadon választható) elméleti feladat (lásd a versenykiírást).

Mérési feladat

M. 218. Készítsünk mágneses ingát! Két mágneskorong egyikét rögzítsük az asztalon, a másikat függesszük fel felette úgy, hogy egyensúlyi helyzetben elég közel legyenek egymáshoz, vonzó helyzetben. Mérjük meg a kitérített ingára ható vonzóerőt a kitérítési szög függvényében! (6 pont)

Közli: Bakonyi Gábor, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok

P. 3364. A marokkói Kalid Kanussi 1999. október 24-én a chicagói maratoni versenyen 2 óra 5 perc 42 másodperc alatt tette meg a 42 195 méter hosszú távot.
a) Hány méterrel ,,maradt le'' a sportoló a 2 órás álomcsúcsot jelentő rekordtól? (Tételezzük fel, hogy állandó nagyságú sebességgel futotta végig a távot.)
b) Mennyivel kellett volna növelnie az átlagsebességét, hogy a napjainkban még hihetetlen csúcsot elérje? (3 pont)

Közli: Kopcsa József, Debrecen (Hatvani István fizikaverseny)

P. 3365. Egy délután Vivi telefonál Péternek, hogy neki már megérkezett a KöMaL októberi száma. Péter elindul Vivihez, s percenként 120 lépést tesz meg. Rögtön visszafordul, és a KöMaL-t olvasva percenként már csak 60 lépést tesz meg, egészen hazáig. Hány lépésre lakik Vivi Pétertől, ha a teljes menetidő oda-vissza 30 perc? (3 pont)

Közli: Simon Péter, Pécs (Dischka Győző fizikaverseny)

P. 3366. Egymással érintkező, R sugarú merev gömbök alkotta köbös kristályrács-modellben mekkora annak a gömbnek a sugara, amely ebben a szerkezetben a gömbök közötti térrészben még elfér? (3 pont)

Zemplén Győző fizikaverseny, Nagykanizsa

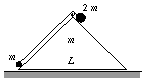
P. 3367. Egy m tömegű, egyenlő szárú derékszögű háromszög keresztmetszetű fahasáb súrlódásmentesen csúszhat a vízszintes felületen. A hasábra az ábrán látható módon fonállal összekötött m és 2m tömegű, pontszerűnek tekinthető testeket helyezünk. A fahasáb alapjának hossza L=54 cm. A súrlódás, valamint a fonál és a csiga tömege elhanyagolható.
A fonállal összekötött testeket egy adott pillanatban elengedjük.
a) Mekkora úton mozdul el a fahasáb, amíg a 2m tömegű test a fahasáb aljára ér?
b) Határozzuk meg a testek és a fahasáb sebességét a 2m tömegű test leérkezésének pillanatában! (6 pont)

Közli: Kotek László, Pécs (Párkányi László fizikaverseny)

P. 3368. Egy literes fazékban, amelynek alja éppen 1 dm² területű, fél liter víz van. Mekkora munkát végzünk, ha egy 0,5 dm² keresztmetszetű, magas főzőpoharat talpával lefelé lassan lenyomunk a fazék fenekére? (A pohár tömege elhanyagolható.) (4 pont)

Károly Ireneusz fizikaverseny, Pécs

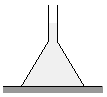
P. 3369. Egy tölcsérbe az ábra szerinti helyzetben 1 dm³ vizet töltünk. Az asztalon a tölcsér által letakart terület 2 dm², a víz magassága 1,2 dm. Legalább mekkora legyen a tölcsér tömege, hogy ne emelkedjék fel az alátámasztási felületről? (4 pont)

Kalamár Csaba emlékverseny, Nagykanizsa

P. 3370. Egy gyakorlott gyöngyhalász h₁ mélységig úszik lefelé, onnan már úszás nélkül is tovább süllyed. A fenékre érve a derekához köt egy, a tartalmával együtt m tömegű, a víznél kétszer nagyobb átlagsűrűségű kosarat, majd elkezd felfelé úszni. Amikor h₂ távol van a vízfelszíntől, nem kell tovább tempóznia, anélkül is felemelkedik. Mekkora a gyöngyhalász tüdejének térfogata? (Merülése közben sehol nem fúj ki levegőt magából.) (5 pont)

Közli: Bodor András, Budapest

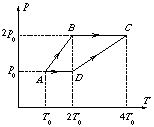P. 3371. Az ábrán ugyanazon N₂ gáz két állapotváltozását láthatjuk nyomás-hőmérséklet grafikonon. Az A állapotban a gáz térfogata V₀.
a) Ábrázoljuk az ABC és az ADC állapotváltozást nyomás-térfogat grafikonon!
b) Melyik folyamatban vesz fel több hőt a gáz?
c) Határozzuk meg a két úton felvett hő arányát! (4 pont)

Nagy László fizikaverseny, Kazincbarcika

P. 3372. Két 30 V méréshatárú voltmérő és egy 1 mA méréshatárú ampermérő van sorbakötve egy telepre. Az egyik voltmérő 12 V-ot, a másik 19 V-ot jelez, az árammérő 0,4 mA-t mutat. Vizsgáljuk meg, mi történik, ha valamelyik műszert rövidre zárjuk! Mit mutatnak ekkor a műszerek? Károsodik-e valamelyikük? (4 pont)

Közli: Radnai Gyula, Budapest

P. 3373. A Naprendszer adatait felhasználva mutassuk meg, hogy az 1999. augusztus 11-i teljes napfogyatkozáskor a Hold árnyéka kb. kétszeres hangsebességgel futott át Magyarországon. (4 pont)

Közli: Korpássy Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. november 13.