Matematikából kitűzött gyakorlatok és feladatok
2000. október

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött (könnyebb) gyakorlatok

C. 595. Melyek azok a háromjegyű számok, amelyek egyenlők a számjegyeik faktoriálisainak összegével?

C. 596. Oldjuk meg a valós számok halmazán az 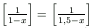egyenletet. ([a], az a egész része az a-nál nem nagyobb egészek legnagyobbika.)

C. 597. Bizonyítsuk be, hogy egy derékszögű háromszögben a beírt és körülírt kör középpontjának távolsága a körülírt kör sugarának legalább a (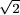-1)-szerese.

C. 598. Van-e 2000 olyan pozitív egész szám, hogy egyikük sem osztható semelyik másikkal, de bármelyikük négyzete osztható az összes többi számmal?

Javasolta: Ábrány Miklós, Ukrajna

C. 599. Egy egyenes kúp alapkörének sugara R, magassága egységnyi. A kúpot az alapjától h távolságra elmetsszük az alapjával párhuzamos síkkal. A levágott kúpot tükrözzük a metsző síkra, majd a csonkakúpból a közös részt eltávolítjuk. Mekkora az így kapott test térfogata?

A B pontversenyben kitűzött feladatok

B. 3392. Adott 25 edény, űrtartalmuk rendre 1,2,...,25 liter. Hányféleképpen választható ki közülük tíz úgy, hogy bármely két kiválasztott edény felhasználásával kimérhető legyen 1 liter víz? (Korlátlan mennyiségű víz áll rendelkezésre, és egyik edényből a másikba is lehet töltögetni.) (4 pont)

Javasolta: Kozma László, Székelyudvarhely

B. 3393. Mekkora az ABC háromszög és az A'B'C' háromszög területének aránya, ha az AA', BB', CC' szakaszok felezőpontjai rendre B', C', A'? (3 pont)

B. 3394. Bizonyítsuk be, hogy pontosan akkor szerkeszthető a, b és c hosszúságú oldalakkal háromszög, ha az a, b, c pozitív valós számokra teljesül, hogy (a²+b²+c²)²>2(a⁴+b⁴+c⁴). (3 pont)

B. 3395. Szerkesszük meg az A₁A₂A₃A₄A₅ ötszöget, ha adott az A_i pontnak az A_i+1 pontra vonatkozó tükörképe (i=1,...,5,A₆:=A₁). (3 pont)

B. 3396. Oldjuk meg az xy+yz+zx-xyz=2 egyenletet, ha x, y és z pozitív egész számok. (4 pont)

B. 3397. ABC egy hegyesszögű háromszög, a KLMN pedig egy olyan téglalap, hogy N az AC szakaszra, K és L pedig az AB szakaszra illeszkedik. Toljuk el a KLMN téglalapot az AC-vel párhuzamosan úgy, hogy M' a BC szakaszra kerül. Így kapjuk a K'L'M'N' téglalapot. Mutassuk meg, hogy CL' és AB metszéspontját az AM és CB metszéspontjával összekötő egyenes merőleges az AB egyenesre. (4 pont)

B. 3398. Az ABCD pontok úgy helyezkednek el a térben, hogy az AB és CD szakaszok hossza 4 egység, míg a BC és DA szakaszok hossza 5 egység. Jelölje az AC és BD szakaszok hosszának négyzetét rendre x és y. Ábrázoljuk a koordináta-rendszerben az így adódó x,y számpárok halmazát. (4 pont)

Javasolta: Hraskó András, Budapest

B. 3399. Adott a síkon két kör, e és f, rajtuk kívül pedig a P pont. A P -ből egy-egy érintőt húzunk a két körhöz, ezek érintési pontja E és F. Bizonyítsuk be, hogy azoknak a szakaszoknak az aránya, amelyeket a két kör metsz ki az EF egyenesből, nem függ attól, hogy melyik két érintőt rajzoltuk meg. (5 pont)

Az e havi lapban a B.3400. feladat téves, 3401. sorszámmal jelent meg.
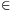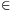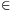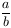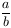
B. 3400. Adott d egész számra legyen S_d={x ²+dy²:x,y Z} . Tegyük fel, hogy a S_d és b S_d olyanok, hogy b prím és egész. Bizonyítsuk be, hogy ekkor 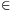S_d. (5 pont)

Javasolta: Csörnyei Marianna, London

B. 3401. Egy nagy, önkiszolgáló raktárban rengeteg árut tárolnak legfeljebb 1 tonnás csomagokban. Van egy 3 és egy 4 tonnás teharautónk. Szerződést akarunk kötni, amelyben vállaljuk, hogy a raktárból egy fordulóval legalább N tonna árut szállítunk el. Mekkora N legnagyobb értéke? (5 pont)

Arany D. versenyfeladat (2000) nyomán

A pontversenyben kitűzött nehezebb feladatok

A. 245. Autónkkal egy kör alakú autópályán kell körbehaladnunk. A pálya mentén bizonyos helyeken benzinkutak vannak, az ezekben található összes üzemanyag két kör megtételére elég. Igazoljuk, hogy a benzinkutak közül kiválasztható legalább egy, amelytől bármelyik irányba elindulva oda visszajuthatunk.

A. 246. Határozzuk meg az összes olyan x,y,z,w valós számnégyest, amelyre

x+y+z+w=x⁷+y⁷+z⁷+w⁷=0.

Shay Gueron, Haifa

A. 247. Igazoljuk, hogy az egységnégyzet oldalegyenesein nincs olyan pont, amely mind a négy csúcstól racionális távolságra van.

Kovács Ádám, Budapest

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

A beküldési határidő: 2000. november 15.