A 2000. novemberi B-jelű matematika feladatok megoldása

Megoldásvázlat. Jelölje l₁, l₂, f₁ és f₂ az első, ill. a második iskolába járó lányok átlagát, ill. az első és a második iskolába járó fiúk átlagát. Hasonlóan jelölje a megfelelő iskolába járó megfelelő nemű gyerekek létszámát L₁, L₂, F₁ ill. F₂. A feladat állítása szerint \(\displaystyle {{l_1}\over{L_1}}=76\), ebből l₁=76L₁. Hasonlóan f₁=71F₁, l₁=90L₂, f₂=81F₂. Ezt a négy állítást felhasználva \(\displaystyle 79={{f_1+f_2}\over{F_1+F_2}}=71+{{10F_2}\over{F_1+F_2}}\), tehát \(\displaystyle 8={{10F_2}\over{F_1+F_2}}\), amiből F₂=4F₁. Hasonlóan \(\displaystyle 3={{5L_1}\over{L_1+F_1}}\), amiből L₁=3/2F₁. Végül az utolsó állítást felhasználva \(\displaystyle 3={{9L_2}\over{L_2+F_2}}\), amiből az előzőek felhasználásával L₂=2F₁. A kérdésre tehát a válasz: \(\displaystyle {{l_1+l_2}\over{L_1+L_2}}={{76L_1+90L_2}\over{L_1+L_2}}=76+{{14L_2}\over{L_1+L_2}}=76+{{14\cdot2F_1}\over{3/2F_1+2F_1}}=84\), azaz a lányok átlaga 84 volt.

B. 3403. Bizonyítsuk be, hogy ha az a, b, c valós számokra 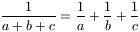, akkor 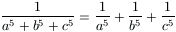. (3 pont)

Javasolta: Székelyhidi Tamás, Ercsi

Megoldásvázlat. Tudjuk, hogy \(\displaystyle {1\over{a+b+c}}={1\over a}+{1\over b}+{1\over c}\). Tehát a, b, \(\displaystyle c\neq0\). Az egyenlet mindkét oldalát abc(a+b+c)-vel megszorozva, majd átrendezve kapjuk, hogy (a+b)(a+c)(b+c)=0. Ebből az következik, hogy a szorzat egyik tényezője 0. A szimmetria miatt feltehető, hogy a+b=0, azaz a=-b. Ekkor viszont a⁵=-b⁵, tehát a bizonyítandó egyenlőség baloldalán és jobboldalán is kiesik az a-t, ill. b-t tartalmazó két tag, a maradék pedig \(\displaystyle {1\over{c^5}}={1\over{c^5}}\) azonosság.

B. 3404. Egy 10 egység élű kocka egyik csúcsából kiinduló három élének végpontja A, B és C. Az ABC síkkal párhuzamos S₁ és S₂ síkok a kockát három részre osztják, melyek térfogatának aránya 251:248:251. Mekkora a két sík távolsága? (5 pont)

Megoldásvázlat. Tekintsük az ABC síkhoz közelebbi metsző síkot, és használjuk az ábra betűzéseit. A síknak a kockából 1004/3 egység térfogatú darabot kell levágnia. Mivel az ABCD tetraéder térfogata ennél kisebb, 1000/6 egység, ezért 10<x<15.

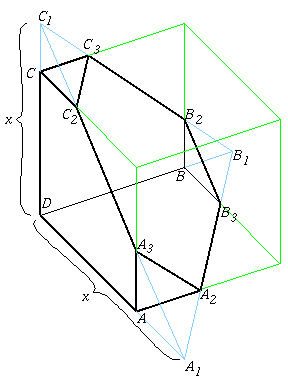
A levágott darab térfogatát úgy számoljuk ki, hogy az A₁B₁C₁D tetraéder térfogatából kivonjuk az AA₁A₂A₃, BB₁B₂B₃ és CC₁C₂C₃ tetraéderek térfogatát. Így a következő egyenletet kapjuk:

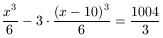
x³-45x²+450x-496=0

(x-31)(x²-14x+16)=0.

A (10,15) intervallumba egyetlen gyök esik: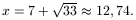

A két sík távolsága pedig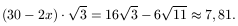

B. 3405. Van öt golyónk. Kilenc mérést hajthatunk végre egy egykarú mérlegen, amelyen egyszerre egy vagy két golyó súlyát mérhetjük meg. Megtörténhet azonban, hogy a kilenc mérés egyikének az eredményét tévesen jegyezzük föl. Megtudhatjuk-e ennek ellenére mind az 5 golyó súlyát? (4 pont)

Javasolta: Surányi László, Budapest

Megoldásvázlat. Jelölje az öt golyót rendre a, b, c, d illetve e. Legyen a kilenc mérés sorra ab, ac, ad, ae, bc, bd, be, cd, a. Ebből a kilenc mérésből mind az öt golyó súlyát meg tudjuk állapítani.

B. 3406. Egy sokszög csúcsainak halmaza olyan (x,y) koordinátájú pontokból áll, amelyekre x és y pozitív egészek, továbbá x|2y+1 és y|2x+1. Mekkora lehet legfeljebb a sokszög területe? (4 pont)

Javasolta: Mihalovics Sándor, Esztergom

Megoldásvázlat. I. eset: x=2y+1. Ekkor y|2(2y+1)+1=4y+3, amiből következik, hogy y|3. Tehát y=1 vagy y=3. Az első esetben x=3, a második esetben x=7.

II. eset: y=2x+1. Ekkor az első esethez hasonlóan kijön, hogy x=1 és y=3 vagy x=3 és y=7.

III. eset: x<2y+1 és y<2x+1.

Tudjuk, hogy d|z esetén, amennyiben \(\displaystyle d\neq z\), akkor \(\displaystyle d\leq\sqrt z\), és ezért d\(\displaystyle ge\)4 esetén \(\displaystyle d\leq{d\over2}\). Ez alapján \(\displaystyle x\leq{{2y+1}\over2}\), azaz x-y\(\displaystyle le\)1/2. Hasonlóan y-x\(\displaystyle le\)1/2, tehát x-y=0. Ekkor x|2x+1 miatt x csak 1 lehet, és ugyanígy y is 1.

Öt pontot kaptunk, melyeket a koordinátarendszerben ábrázolva az általuk meghatározott terület is könnyen kiszámítható: \(\displaystyle t=6^2-2\cdot{{2\cdot4}\over2}-{{4\cdot4}\over2}=20\).

B. 3407. Arnold, Bendegúz, Cézár, Dorottya, Egon és Ferdinánd szerepjátékhoz készülődik. Még nem döntötték el, melyikük legyen a kalandmester. (Ebben a játékban egyikük a kalandmester, a többiek alkotják a csapatot.) A kalandmester személyéről sorsolással kívánnak dönteni, ehhez a játékban használt 10 oldalú ,,dobókockával'' dobnak a következőképpen:

Előre meghatározott sorrendben mindenki egyszer dob a kockával. Az lesz a kalandmester, aki először 1-est, vagy 2-est dob. Ha a kör végére nincs meg a kalandmester, akkor újra kezdik ugyanebben a sorrendben a dobásokat mindaddig, amíg valaki 1-est vagy 2-est nem dob.

Dorottya még sohasem vezetett ebben a társaságban játékot, és most nagyon szeretne. A fiúk udvariasak és megengedik neki, hogy megválassza azt, hogy hányadiknak dob. Te mit javasolnál Dorottyának? (3 pont)

Javasolta: Pogány Gyula, Szolnok

Megoldásvázlat. Annak a valószínűsége, hogy az első játékos lesz a kalandmester \(\displaystyle {2\over{10}}\). Annak a valószínűsége, hogy a 2.: \(\displaystyle (1-{2\over{10}})\cdot{2\over{10}}\). Annak a valószínűsége, hogy az n. dobásnál jön ki először az 1-es vagy a 2-es: \(\displaystyle (1-{2\over{10}})^{n-1}\cdot{2\over{10}}\). Tehát minden körben, ha addig nem dobtak sem 1-est, sem 2-est, az első játékosnak van erre a legnagyobb esélye. Így Dorottya, ha kalandmester szeretne lenni, dobjon elsőnek.

B. 3408. Egy szabályos 2n oldalú sokszög minden csúcsára egy-egy egész számot írunk úgy, hogy a szomszédos csúcsokra írt számok különbsége 1. Nevezzük hegyszámnak azokat a számokat, amelyek nagyobbak mindkét szomszédjuknál és völgyszámnak azokat, amelyek kisebbek mindkét szomszédjuknál. Bizonyítsuk be, hogy a hegyszámok összegéből a völgyszámok összegét levonva n-et kapunk. (5 pont)

Javasolta: Hraskó András, Budapest

Megoldásvázlat.

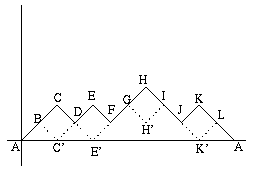
1. eset: A C pontot hajtjuk le. Ekkor a változások: k-(k-1) helyett (k-1)-(k-2), de mivel mindkettő 1, ezért az összegben nincs változás.

2. eset: Az E pontot hajtjuk le. Ekkor a változások: k-2(k-1) helyett -(k-2), amik egyenlőek.

3. eset: A H pontot hajtjuk le. A változások: k+1 helyett 2k-(k-1)=k+1.

4. eset: A K pontot hajtjuk le. Ez ugyanazt az eredményt adja, amit az 1. esetben kaptunk.

Tehát egy ``lehajtás'' sem változtat az eredményen. Ugyanígy az sem, ha egy völgyszámot hajtunk föl. Föl- és lehajtásokkal pedig véges sok lépésben elérhető az az állapot, amikor mindig 1-gyel nőnek, majd 1-gyel csökkennek a szomszédos csúcsokra írt számok (természetesen az A csúcsra írt számot nem változtatjuk meg). Ekkor az A csúcsra írt számot m-mel jelölve a keresett különbség valóban n^.(m+1)-nm=n.

B. 3409. Tükrözzük az y=x² parabolát az (1;1) pontra. Mi a tükörkép egyenlete? (3 pont)

Megoldásvázlat. A tükörkép egy lefele álló parabola lesz, melynek maximumpontja megegyezik az y=x² egyenletű parabola minimumpontjának, a (0,0) pontnak az (1,1) pontra vonatkozó tükörképével. Ez a pont a (2,2), és így a kapott parabola egyenlete y=-(x-2)²+2.

B. 3410. Egy három méter magas nagy festmény függ a falon, alsó széle egy méterrel van a néző szemmagassága felett. A kép látványa annál élvezhetőbb, minél nagyobb az a függőleges szög, amelyben látszik. Milyen távolságból nézve lesz ez a szög a lehető legnagyobb? (4 pont)

Megoldásvázlat.

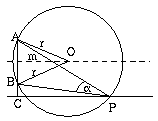
Vegyünk egy, a kép síkjára merőleges síkmetszetet. Jelölje A és B a metszeten a kép két szélét, P pedig azt a pontot, ahonnan nézzük. Rajzoljuk meg az ABP köré írható kört. Ennek középpontját O-val jelölve a kerületi- középponti szögek tétele miatt \(\displaystyle \alpha={{AOB\measuredangle}\over2}\). Tehát \(\displaystyle alpha\) akkor a lehető legnagyobb, ha \(\displaystyle AOB\measuredangle\) a lehető legnagyobb, azaz, ha O a lehető legközelebb van AB egyeneséhez, de AO nem kisebb, mint O és CP egyenes távolsága.

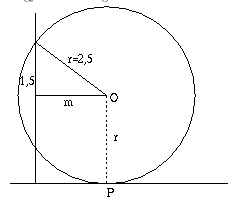
Ez a távolság (3+1)-3/2=2,5=r. Ekkor \(\displaystyle CP=m=\sqrt{r^2-(3/2)^2}=\sqrt{2,5^2-1,5^2}=2\) a Pitagorasz-tétel miatt. Tehát 2 méteres távolságból nézve lesz a szög a lehető legnagyobb.

B. 3411. Legalább hány oldalú az a szabályos sokszög, amely körülírt körének területét 1 ezreléknél kisebb hibával közelíti? (4 pont)

Megoldásvázlat. Az r sugarú kör területe t_k=r²\(\displaystyle pi\), a beleírt n oldalú szabályos sokszögé pedig \(\displaystyle t_n=n\cdot1/2\cdot r^2\cdot\sin{{2\pi}\over n}\). Az a kérdés, hogy mely n-re lesz \(\displaystyle {{t_k-t_n}\over{t_k}}\leq0.001\). Átalakítva: 0,999t_k\(\displaystyle le\)t_n, ami n=81 esetén még nem, n=82 esetén pedig már teljesül. Tehát legalább 82 oldalú sokszögről van szó.