Matematikából kitűzött gyakorlatok és feladatok
2000. november
Kérjük, olvassa el a versenykiírást.
 |
A C pontversenyben kitűzött (könnyebb) gyakorlatok |
C. 600. Személygépkocsival utazunk Budapestről Kassa felé állandó sebességgel. Meglátunk egy kilométert jelző táblát, amin egy kétjegyű szám van. Fél óra múlva olyan táblához érünk, amelyen az előbbi számjegyek állnak fordított sorrendben. Újabb 30 perc múlva olyan táblához érünk, amelyen a két eddigi számjegyen kívül még egy 0 is van. Mekkora sebességgel haladunk?
C. 601. Oldjuk meg a következő egyenletet:
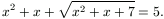
Javasolta: Gyanta Nándor, Budapest
C. 602. Legkevesebb hány egységkockából lehet összerakni egy nagy kockát úgy, hogy belül legyen a kis kockáknak több, mint a fele?
C. 603. Határozzuk meg az f(x)=(x2+x+1)/(x2+1) függvény értékkészletét.
C. 604. Az ABC háromszög beírt körének középpontja O, területe pedig t. Mutassuk meg, hogy
2t=AO2sin +BO2sin
+BO2sin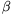 +CO2sin
+CO2sin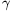 .
.
Javasolta: Mihalovics Sándor, Esztergom
 |
A B pontversenyben kitűzött feladatok |
B. 3402. Két iskola diákjai egy teszten a következő eredményt érték el:
B. 3403. Bizonyítsuk be, hogy ha az a, b,
c valós számokra 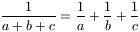 , akkor
, akkor 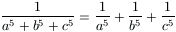 . (3 pont)
. (3 pont)
Javasolta: Székelyhidi Tamás, Ercsi
B. 3404. Egy 10 egység élű kocka egyik csúcsából kiinduló három élének végpontja A, B és C. Az ABC síkkal párhuzamos S1 és S2 síkok a kockát három részre osztják, melyek térfogatának aránya 251:248:251. Mekkora a két sík távolsága? (5 pont)
B. 3405. Van öt golyónk. Kilenc mérést hajthatunk végre egy egykarú mérlegen, amelyen egyszerre egy vagy két golyó súlyát mérhetjük meg. Megtörténhet azonban, hogy a kilenc mérés egyikének az eredményét tévesen jegyezzük föl. Megtudhatjuk-e ennek ellenére mind az 5 golyó súlyát? (4 pont)
Javasolta: Surányi László, Budapest
B. 3406. Egy sokszög csúcsainak halmaza olyan (x,y) koordinátájú pontokból áll, amelyekre x és y pozitív egészek, továbbá x|2y+1 és y|2x+1. Mekkora lehet legfeljebb a sokszög területe? (4 pont)
Javasolta: Mihalovics Sándor, Esztergom
B. 3407. Arnold, Bendegúz, Cézár, Dorottya, Egon és Ferdinánd szerepjátékhoz készülődik. Még nem döntötték el, melyikük legyen a kalandmester. (Ebben a játékban egyikük a kalandmester, a többiek alkotják a csapatot.) A kalandmester személyéről sorsolással kívánnak dönteni, ehhez a játékban használt 10 oldalú ,,dobókockával'' dobnak a következőképpen:
Előre meghatározott sorrendben mindenki egyszer dob a kockával. Az lesz a kalandmester, aki először 1-est, vagy 2-est dob. Ha a kör végére nincs meg a kalandmester, akkor újra kezdik ugyanebben a sorrendben a dobásokat mindaddig, amíg valaki 1-est vagy 2-est nem dob.
Dorottya még sohasem vezetett ebben a társaságban játékot, és most nagyon szeretne. A fiúk udvariasak és megengedik neki, hogy megválassza azt, hogy hányadiknak dob. Te mit javasolnál Dorottyának? (3 pont)
Javasolta: Pogány Gyula, Szolnok
B. 3408. Egy szabályos 2n oldalú sokszög minden csúcsára egy-egy egész számot írunk úgy, hogy a szomszédos csúcsokra írt számok különbsége 1. Nevezzük hegyszámnak azokat a számokat, amelyek nagyobbak mindkét szomszédjuknál és völgyszámnak azokat, amelyek kisebbek mindkét szomszédjuknál. Bizonyítsuk be, hogy a hegyszámok összegéből a völgyszámok összegét levonva n-et kapunk. (5 pont)
Javasolta: Hraskó András, Budapest
B. 3409. Tükrözzük az y=x2 parabolát az (1;1) pontra. Mi a tükörkép egyenlete? (3 pont)
B. 3410. Egy három méter magas nagy festmény függ a falon, alsó széle egy méterrel van a néző szemmagassága felett. A kép látványa annál élvezhetőbb, minél nagyobb az a függőleges szög, amelyben látszik. Milyen távolságból nézve lesz ez a szög a lehető legnagyobb? (4 pont)
B. 3411. Legalább hány oldalú az a szabályos sokszög, amely körülírt körének területét 1 ezreléknél kisebb hibával közelíti? (4 pont)
 |
A pontversenyben kitűzött nehezebb feladatok |
A. 248. Hányféleképpen lehet egy n-elemű halmaz hatványhalmazát két diszjunkt részre: az I és H halmazokra bontani úgy, hogy a következő feltételek egyszerre teljesüljenek?
a) tetszőleges a, b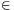 I esetén
a
I esetén
a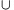 b
b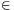 I és
a
I és
a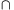 b
b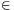 I;
I;
b) tetszőleges a, b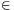 H esetén
a
H esetén
a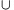 b
b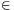 H és
a
H és
a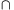 b
b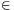 H;
H;
c) tetszőleges a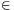 I, b
I, b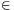 H esetén a
H esetén a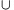 b
b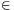 I és a
I és a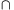 b
b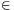 H.
H.
(Egy halmaz hatványhalmazának az összes részhalmazainak halmazát nevezzük.)
Javasolta: Csirmaz Előd, Budapest
A. 249. Legyenek a, b, c, t pozitív számok és abc=1. Igazoljuk, hogy
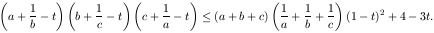
A. 250. Tekintsük a Hanoi tornyai néven közismert játék négytornyos változatát: n darab különböző méretű korong egymásra van helyezve nagyság szerint sorban úgy, hogy alul van a legnagyobb, felül a legkisebb. A korongokat egy másik helyre kell áthelyezni a következő szabályok betartásával:
Bizonyítsuk be, hogy a szükséges minimális lépésszám legalább 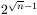 és kisebb, mint
és kisebb, mint 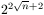 .
.
Énekes Béla (Tolna) ötletéből
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
Bolyai János Matematikai Társulat (KöMaL feladatok); Budapest, Pf. 433. 1371
illetve
megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

