A 2001. májusi B-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

B. 3462. Milyen n-ekre érhető el, hogy a 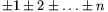alakú összegek között szerepeljen a 100? (3 pont)

Megoldás. Az első n darab természetes szám öszege $\displaystyle S_n={{n(n+1)}\over2}$. Mivel S_n értékét mindig egy szám kétszeresével csökkentjük, ezért a 100-at csak páros S_n-ből kiindulva érhetjük el. S₁₃=91 még kevés, S₁₄=105 páratlan, viszont S₁₅=120, így ha az összegben a 10 előjelét negatívra változtatjuk, akkor pont 100 lesz az eredmény: 1+2+3+4+5+6+7+8+9-10+11+12+13+14+15=100. S₁₆=136, 8+10=36/2, így 1+2+3+4+5+6+7-8+9-10+11+12+13+14+15+16=100. Bármely négy egymást követő egész szám előjele változtatható úgy, hogy az így kapott négy szám összege 0 legyen: a-(a+1)-(a+2)+(a+3)=0, így ha n=4k+15 vagy n=4k+16 ($\displaystyle k\geq0$), akkor meg tudjuk változtatni az előjeleket a kívánt módon.

Ha n=4k+1, akkor $\displaystyle S_n={{(4k+1)(4k+2)}\over2}=(4k+1)(2k+1)$, ami páratlan. Ha n=4k+2, akkor $\displaystyle S_n={{(4k+2)(4k+3)}\over2}=(2k+1)(4k+3)$, ez is páratlan, ezekre az n-ekre tehát nem kaphatunk 100-at.

Összegezve: pontosan akkor kaphatunk 100-at, ha n=4k ($\displaystyle k\geq4$), vagy ha n=4k+3 $\displaystyle (k\geq3)$.

B. 3463. Egy félkör alakú szivaccsal, amelynek átmérője 20 cm, végigtöröljük egy szoba padlójának egy sarkát úgy, hogy az átmérő két végpontja folyamatosan érinti a szoba derékszöget bezáró két falát. Mekkora területet töröl fel eközben a szivacs? (3 pont)

Megoldás. Az AB átmérőjű félkörív a szivacs. Ha A az x tengelyen, B az y tengelyen mozog, akkor az AB átmérőjű kör átmegy O-n. Ezért az O középpontú, 20 cm sugarú negyedkörön kívüli pontok nem érhetők el a szivaccsal. Az O középpontú, 10 cm sugarú negyedkör belső pontjai lefedhetők az x, ill. y tengelyen nyugvó félkörökkel. Ha a P pont a két negyedkör között van, akkor azzal a félkörrel fedhető le O, amelyhez tartozó teljes kör egyik átmérője tartalmazza OP-t.

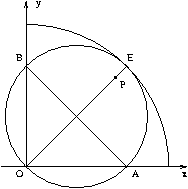
B. 3464. Hány olyan n-jegyű szám van, amelyben a számjegyek összege 9n-8? (4 pont)

Megoldás. Ha minden számjegy 9-es, akkor a számjegyek összege 9n. Ennél 8-cal kisebb számot úgy érhetünk el, ha bizonyos számjegyeket lecsökkentünk, de úgy, hogy a csökkentések összege 8 legyen. Ezt a feladatot tekinthetjük úgy is, mintha az n darab 9-esből kellene kiválasztani 8-at úgy, hogy egy számjegy többször is szerepelhet, és egy számjegy kiválasztása annak 1-gyel való csökkentését jelenti. Ez n elem 8-adrendű ismétléses kombinációja, azaz 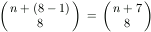olyan n-jegyű szám van, amelyben a számjegyek összege 9n-8.

B. 3465. Az egységoldalú ABCD négyzet AB oldalán lévő E és az F pontokra $\displaystyle AE={1\over n}$ és $\displaystyle BF={1\over m}$, ahol m és n pozitív egész számok. A B pontból kiinduló, AB-vel 30^o-os szöget bezáró egyenes érinti az EF, mint átmérő fölé, a négyzet belsejébe rajzolt félkört. Határozzuk meg az m és n értékét. Van-e a kapott számpárok között olyan, amely mellett a félkör érinti az AC átlót is? (3 pont)

Javasolta: Bíró Bálint, Eger

Megoldás. Ha n=1, akkor E a B pontba kerül, így a félkör érintője a BC oldalegyenes lesz, nem pedig a kívánt egyenes.

Ha m=1, $\displaystyle n\neq1$, akkor

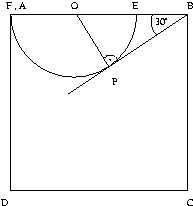
az OPB derékszögű, 30^o-os háromszögből $\displaystyle {{OB}\over{OP}}=2$, és így AO=OE=OP miatt AO=OE=EB=1/3. Ezek szerint AE=2/3=1/n, tehát n nem egész, ami nem lehet.

Ha m=n=2 akkor E és F egybeesik, tehát nem jön létre kör. Így feltehetjük, hogy m és n közül az egyik legalább 2, a másik pedig 2-nél nagyobb.

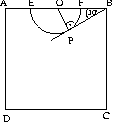
Az első esethez hasonlóan $\displaystyle {{OB}\over{OP}}=2$, valamint OF=OP, amiből EO=OF=FB, s ezért $\displaystyle 1/m=FB={1\over3}EB={1\over3}(1-AE)={1\over3}(1-1/n)$. Ebből $\displaystyle m=3+{3\over{n-1}}$. Mivel m egész, ezért n-1|3. Figyelembe véve, hogy n pozitív, ebből n=4 vagy n=2 adódik. Az első esetben m=4, a másodikban m=2.

I. eset

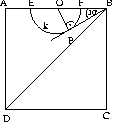
Ha az AC átló érinti k-t, akkor a BD átló is érinti. Viszont ekkor a B pontból két érintőt húzhatnánk k-hoz, ami lehetetlen.

II. eset

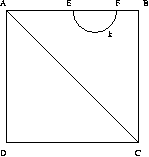
Ebben az esetben sem érinti az AC átló k-t.

B. 3466. Határozzuk meg az ABCD négyzet síkjában azon pontok mértani helyét, amelyekre sin APB$\displaystyle szog$=sin DPC$\displaystyle szog$. (4 pont)

Megoldás. Mivel mindkét szög 0^o és 180^o között van, ezért szinuszuk két esetben lehet egyenlő: vagy egyenlő a két szög is, vagy egymás kiegészítő szögei. Az első esetben a látóköríveket berajzolva látható, hogy P a négyzet középvonalán helyezkedik el. Minden ilyen pont megfelelő.

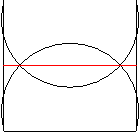
A második esetben, ha a P pont a négyzeten belül helyezkedik el, akkor

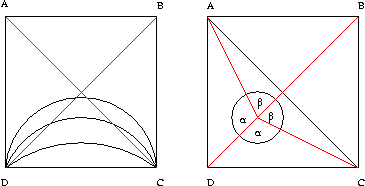
minden köríven pontosan két jó pont található, a jobboldali ábráról leolvasható, hogy ezek a pontok az átlókon helyezkednek el, hiszen $\displaystyle alpha$+$\displaystyle beta$=180^o.

Amennyben a két szög összege 180^o, de P a négyzeten kívül helyezkedik el, akkor

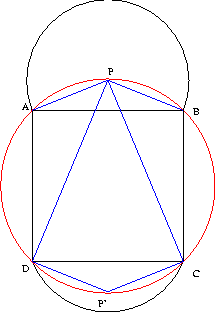
ez csak úgy lehet, ha P rajta van a négyzet köré írt körön. Ha rajta van, akkor $, tehát a köré írt kör bármely pontja jó (A-t, B-t, C-t és D-t kivéve).

Összegezve: a keresett pontok mértani helye a négyzet két középvonala, két átlója és köré írt köre, kivéve a négyzet négy csúcsát.

B. 3467. Keressük meg az x(1+x)(3-x) kifejezés maximumát a pozitív számok körében a differenciálszámítás alkalmazása nélkül. (4 pont)

(A feladat megoldása előtt ajánljuk Csete Lajos 267. oldalon kezdődő cikkének elovasását.)

Megoldás. Ha x nagyobb, mint 0, akkor az első két tényező pozitív, így a maximum keresésekor föltehető, hogy a harmadik tényező, (3-x) is az, az f(x)=x(1+x)(3-x) függvény maximumát tehát a (0;3) nyílt intervallumon keressük. A számtani és mértani közepek közti egyenlőtlenség közvetlenül nem alkalmazható, hiszen a tényezők összege, 4+x függ az x-től. A hivatkozott cikkben mutatott elemi megközelítés sem működik, sőt, a szokásos ,,szorzási'' trükk is elakad. Ez utóbbinak az a lényege, hogy valamelyik tényezőt egy határozatlan t szorzóval kiegészítve az így módosított három tényező összegéből már kiesik a változó. A t értéke az első két tényező mindegyikére a triviális 0, a harmadik tényezőre ugyan t=2 és így x+(1+x)+2(3-x)=7 valóban konstans, tehát a számtani és mértani közepek közti egyenlőtlenség szerint 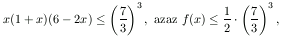azonban most az első két tényező, x és 1+x nem lehetnek egyenlők, a felhasznált egyenlőtlenségben nem állhat egyenlőség és így a kapott becslés nem a keresett maximum, hanem egy felső korlát.

Finomítsuk a fenti trükköt, a keresett szorzót bontsuk tovább két határozatlan tényező, u és v szorzatára, vizsgáljuk az u^.v^.f(x)=(ux)^.(v(1+x))^.(3-x) szorzat három tényezőjét. Feltételeink a következők:

a) u és v pozitív;

b) a tényezők összege, ux+v(1+x)+(3-x) állandó;

c) az ux=v(1+x)=(3-x) egyenletrendszernek létezik pozitív megoldása.

b)-ből u+v=1. Ezt c-be helyettesítve az ux=(1-u)(1+x) egyenlet megoldása $\displaystyle x={{u-1}\over{1-2u}},$ az ux=3-x egyenleté pedig $\displaystyle x={3\over{u+1}}.$ E két megoldás egyenlőségéből pedig az u²+6u-4=0 egyenlet adódik, ennek pozitív gyöke $\displaystyle u=\sqrt{13}-3$. (Ekkor mindkét, az x-re kapott tört értelmes.) Ha tehát $\displaystyle v=1-u=4-\sqrt{13}$, akkor láthatóan v is pozitív, ux+v(1+x)+(3-x)=3+v és van olyan - pozitív - x, mégpedig $\displaystyle {3\over{u+1}}={{\sqrt{13}+2}\over3}\approx1,8685$, hogy az (ux)^.(v(1+x))^.(3-x) szorzat tényezői egyenlők. A számtani és a mértani közepek közti egyenlőtlenség szerint tehát $\displaystyle \root3\of{uvf(x)}\leq{{3+v}\over3}$ és most pontosan akkor van egyenlőség, ha $\displaystyle x={{\sqrt{13}+2}\over3}.$ A maximum értéke most már adódik akár behelyettesítéssel, akár pedig úgy, hogy az egyenlőtlenség jobb oldalának a köbét elosztjuk uv-vel. Az eredmény összevonás és egyszerűsítés után $\displaystyle {2\over{27}}(13\sqrt{13}+35)\approx6,0646$.

B. 3468. Egy konvex tízszög semelyik három átlója sem megy át egy ponton, és egy, a sokszög belsejében lévő P pont egyik átlón sincs rajta. Mutassuk meg, hogy a sokszög csúcsai közül legalább 28-féleképpen választható ki négy úgy, hogy az általuk meghatározott négyszög tartalmazza P-t. (5 pont)

Megoldás. A négyszöget egy csúcsából kiinduló átlókkal 8 háromszögre felosztva P pontosan egy háromszögben van benne.

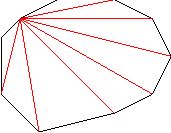
Ezt az eljárást mind a 10 csúcsból elvégezve 10 olyan háromszöget kapunk, melynek P eleme. A kérdés az, hogy ebből hány egyezhet meg.

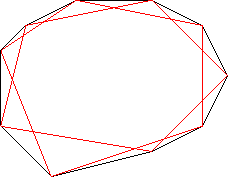
Az eljárások során azok a háromszögek szerepeltek többször (pontosan kétszer), melyeknek csúcsai szomszédosak. Ilyen háromszögből 10 darab van. Ezek közül legfeljebb kettőnek lehet P egyszerre eleme, amiből az is következik, hogy a 10 háromszög közül, melynek P eleme, legfeljebb kettő szerepelhetett duplán. Tehát a 10 háromszögből 10-2=8 biztosan különböző. Mindegyik háromszög esetén a negyedik csúcsot 10-3=7-féleképpen választhatjuk ki. Ez összesen 8^.7=56 négyszög. Egy négyszöget egy átlója két négyszögre bont fel, melyek közül P pontosan az egyikben szerepel. Ebből következik, hogy egy négyszög legfeljebb kétszer szerepelhetett az összeszámlálásban, tehát valóban legalább 56/2=28 négyszögben szerepel P.

B. 3469. Határozzuk meg mindazokat a folytonos f függvényeket, amelyekre f(f(x))=x+f(x) minden x valós számra. (5 pont)

Gillis-Turán matematikaverseny, 2001

Megoldás. A függvényegyenletből következik, hogy f kölcsönösen egyértelmű. Ha f(x)=x, akkor ugyancsak az egyenletből: x=2x, azaz x=0. Ha pedig f folytonos és kölcsönösen egyértelmű, akkor vagy szigorúan monoton növő, vagy pedig szigorúan monoton fogyó. Ha növő, akkor f előjele megegyezik az x, ha pedig fogyó, akkor a -x előjelével.

Tetszőleges nemnegatív egészre jelölje f⁽ⁿ⁾ az f függvény n-edik iteráltját - tehát legyen f⁽⁰⁾(x)=x és f⁽ⁿ⁺¹⁾(x)=f(f⁽ⁿ⁾(x)). Ekkor teljes indukcióval nyilvánvaló, hogy

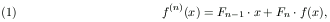
ahol F_n a Fibonacci sorozat, F₀=0, F₁=1, F_n+2=F_n+1+F_n.

Vizsgáljuk először azt az esetet, amikor az f szigorúan monoton fogyó. Ilyenkor az ellenkező előjelű x és f(x) összege az x-szel egyező előjelű f(f(x)), tehát |f(x)|<|x|, az f⁽ⁿ⁾(x) sorozat korlátos. Ebből következik, hogy az (1) egyenlőséget a végtelenhez tartó F_n sorozattal osztva egy 0-hoz tartó sorozatot kapunk, amit átrendezve

$\displaystyle {{F_{n-1}}\over{F_n}}x\mapsto-f(x).$

Ismeretes, hogy az $\displaystyle {{F_n}\over{F_{n_1}}}$ arány az x²-x-1=0 egyenlet pozitív gyökéhez, a $\displaystyle \gamma={{1+\sqrt5}\over2}$ számhoz tart és így a függvényegyenlet egyetlen folytonos szigorúan monoton fogyó megoldása $\displaystyle f(x)=-{1\over{\gamma}}\cdot x$.

Ha az f szigorúan monoton növő, akkor könnyen látható, hogy akármilyen nagy és akármilyen kicsi értékeket is fölvesz (f(f(x))>x, ha x pozitív és f(f(x))<x, ha x negatív), és így az inverze, g, amely szintén folytonos, mindenütt értelmes. A függvényegyenlet szerint teljesül rá, hogy x=g(g(x))+g(x), innen pedig indukcióval (-1)ⁿg⁽ⁿ⁾(x)=F_n-1^.x-F_n^.g(x). Most |g(x)|<|x|, megint oszthatunk F_n-nel és kapjuk, hogy $\displaystyle {{F_{n_1}}\over{F_n}}x\mapsto g(x)$, azaz $\displaystyle g(x)={1\over{\gamma}}x$, tehát a megoldás a g inverzeként f(x)=$\displaystyle gamma$x.

A feladatnak tehát két megoldása van: $\displaystyle f_1(x)={{1+\sqrt5}\over2}\cdot x$ és $\displaystyle f_2(x)={{1-\sqrt5}\over2}\cdot x$.

B. 3470. Írjuk föl annak az egyenesnek az egyenletét, amely az y=3x⁴-4x³ egyenletű görbét két különböző pontban érinti. (4 pont)

Megoldás. Az f:x$\displaystyle mapsto$3x⁴-4x³ függvény grafikonjának érintő egyenese, amely teljesíti a feladat feltételeit legyen az e:x$\displaystyle mapsto$ax+b függvény grafikonja. Az érintési pontok első koordinátája legyen c és d. Az f-e függvény zérus helyei szintén c éd d. Ezeken a helyeken az x tengely érinti is az f-e függvény grafikonját, tehát c és d kétszeres zérus helyei az f-e függvénynek, így felírható a következő egyenlőség: 3x⁴-4x³-ax-b=3(x-c)²(x-d)², amiből $\displaystyle x^4-{4\over3}x^3-{a\over3}x-{b\over3}=(x^2-2cx+c^2)(x^2-2dx+d^2)$ adódik. Elvégezve a szorzást a következőt kapjuk:

$\displaystyle x^4-{4\over3}x^3-{a\over3}x-{b\over3}=x^4-2(c+d)x^3+(c^2+4cd+d^2)x^2-2(c^d+cd^2)x+c^2d^2,$

amiből az együtthatók egyenlősége miatt a következő egyenletrendszer adódik: $\displaystyle -{4\over3}=-2(c+d)$

0=c²+4cd+d²

$\displaystyle -{a\over3}=-2(c^d+cd^2)$

$\displaystyle -{b\over3}=c^2d^2$.

Az egyenletekből mindegyik ismeretlen meghatározható, azonban c éd d meghatározható a és b ismerete nélkül is. Az első két egyenletből kapjuk, hogy c+d=2/3, cd=-2/9, amit felhasználva a harmadik és a negyedik egyenletben, a-ra és b-re a következő adódik: $\displaystyle b=-{4\over{27}}$, a=-8/9. Ebből $\displaystyle c={{2+2\sqrt3}\over3}$, $\displaystyle d={{2-2\sqrt3}\over3}$. A keresett egyenes egyenlete tehát $\displaystyle y=-{8\over9}x-{4\over{27}}$, és ez jó is.

B. 3471. Egy hangya mászkál az x²+y²+xy=6 egyenletű görbe által határolt területen. Útvonala a koordinátatengelyekkel párhuzamos egyenes szakaszokból áll. A hangya a görbe tetszőleges pontjából kiindulva addig megy egyenesen a görbe belsejében, amíg újra eléri a görbe határát. Ekkor 90^o-kal elfordul és folytatja útját a görbe belsejében. A hangya csak akkor áll meg, ha olyan határponthoz ér, amelyben már járt, vagy ha nem tudja útját a fenti szabálynak megfelelően folytatni. Bizonyítsuk be, hogy függetlenül a kiindulási ponttól a hangya előbb-utóbb megáll. (5 pont)

Gillis-Turán matematikaverseny, 2000

Megoldás. Könnyen ellenőrizhető, hogy az adott egyenletű görbe egy ellipszis, amelynek a tengelyei 45^o-os szöget zárnak be a koordinátatengelyekkel. Forgassuk el a görbét - és a hangya útvonalát is - 45^o-kal, ekkor egyenlete $\displaystyle {{x^2}\over{12}}+{{y^2}\over4}=1$ alakú lesz. A hangya útvonala az elforgatott tartományon ekkor a koordinátatengelyekkel 45^o-os szöget bezáró szakaszokból álló töröttvonal. Az ellipszis excentricitása $\displaystyle {b\over a}={1\over{\sqrt3}}$, így ha a tartományra - és a hangya útvonalára is - $\displaystyle \sqrt3$ arányú merőleges affinitást alkalmazunk, akkor az ellipszis origó közepű körbe megy át, a hangya útvonala pedig olyan töröttvonalba, amelynek szomszédos szakaszai az x-tengellyel 60^o, illetve -60^o-os szöget zárnak be. A hangya két egymást követő lépése utáni helyzetét így megkaphatjuk, ha útvonalának kezdőpontját elforgatjuk 120^o-kal a kör középpontja körül. Hat egymást követő lépés után tehát a hangya éppen visszajut oda, ahonnan elindult és így valóban megáll.

Ez majdnem minden kezdőpontra teljesül, annak a négy pontnak a kivételével, amelyekben az x-tengellyel 60^o, illetve -60^o-os szöget bezáró érintők érintik a kört. Az eredeti ellipszisen ezek a pontok a koordinátatengelyekkel párhuzamos érintők érintési pontjai. Ha a hangya e négy pont valamelyikéből indul, akkor két lépés után egy másik ilyen pontba érkezik és ilyenkor merőlegesen elfordulva az érintő mentén kellene továbbhaladnia, tehát nem tudná a tartomány belsejében folytatni az útját és így az utasítás szerint szintén megáll.