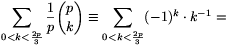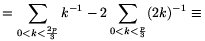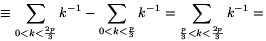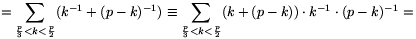|
Solutions for problems "A" in September, 2001 |
In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.
A. 269. A round hole is to be completely covered with two square boards. The sides of the squares are 1 metre. In what interval may the diameter of the hole vary?
Solution. It is easy to see that a hole of radius \(\displaystyle 2-\sqrt2\) (and all smaller holes) can be covered by two unit squares, see Figure 1.
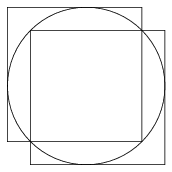
Figure 1
We will prove that if a unit square covers at least half of the perimeter of a circle of radius r, then \(\displaystyle r\le2-\sqrt2\). This implies that the diameter of the hole cannot exceed \(\displaystyle 4-2\sqrt2\approx1.17\) metre.
Let K be a circle of radius r, and N be a unit square, which covers at least the half of K. If r\(\displaystyle ge\)1/2, then N can be translated such that each side of N or its extension has at least one common point with K and the covered part of the curve is increasing, see Figure 2.
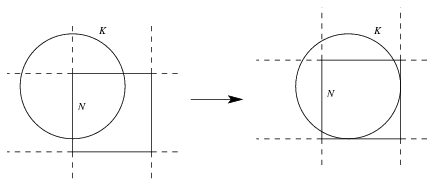
Figure 2
So, it can be assumed that r>1/2 and (the extension of) each side of N has a common point with K.
First, consider the case when a vertex of N is inside K. Let the vertices of N be A, B, C, D and suppose that A is inside K. Denote the intersecion of K and the half-lines AB and AD by P and Q, respectively. (Figure 3.)
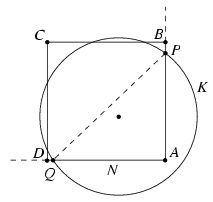
Figure 3
Because PAQ\(\displaystyle angle\)=90o, the centre of K and vertex A are on the same side of line PQ. This implies that the uncovered arc PQ is longer than the half of K. This is a contradiction, thus this case is impossible.
We are left to deal the case when there are no vertices of N inside K and each side or its extension has a common point with K. It is easy to check that these common points cannot be on the extension of the sides of N; they must lie on the perimeter of N.
Denote by \(\displaystyle alpha\), \(\displaystyle beta\), \(\displaystyle gamma\) and \(\displaystyle delta\) the angles drawn in Figure 4.
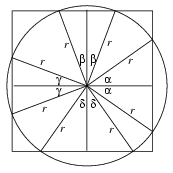
Figure 4
The total of the uncovered arcs is at most the half of K, so \(\displaystyle alpha\)+\(\displaystyle beta\)+\(\displaystyle gamma\)+\(\displaystyle delta\)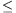 90o. By symmetry, it can be assumed that
90o. By symmetry, it can be assumed that 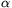 +
+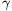
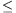 45o.
45o.
As can be read from the Figure, r(cos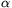 +cos
+cos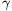 )=r(cos
)=r(cos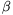 +cos
+cos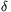 )=1. The concavity of the cosine function yields
)=1. The concavity of the cosine function yields
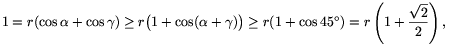
and hence 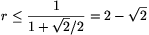 .
.
Thus, the radius of the hole can be at most 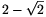 ; its diameter can be at most
; its diameter can be at most 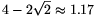 metre.
metre.
A. 270. Prove that if a, b, c, d are positive numbers then
| (1) | 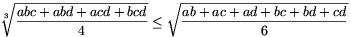 |
Solution 1. Define the folowing symmetric expressions of a, b, c, d:
S33=a3b3+a3c3+a3d3+b3c3+b3d3+c3d3;
S321=a3b2c+a3b2d+...+bc2d3;
S3111=a3bcd+ab3cd+abc3d+abcd3;
S222=a2b2c2+a2b2d2+a2c2d2+b2c2d2;
S2211=a2b2cd+a2bc2d+a2bcd2+ab2c2d+ab2cd2+abc2d2.
Taking the 6th power of (1), we obtain
| (2) | 2S33+6S321+12S3111 15S222+24S2211. 15S222+24S2211. |
By the A.M.-G.M. inequality
2S33=(a3b3+a3c3+b3c3)+(a3b3+a3d3+b3d3)+
+(a3c3+a3d3+c3d3)+(b3c3+b3d3+c3d3)
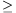 3a2b2c2+3a2b2d2+3a2c2d2+3b2c2d2=3S222.
3a2b2c2+3a2b2d2+3a2c2d2+3b2c2d2=3S222.
We similarly obtain that S321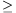 6S222, S321
6S222, S321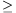 4S2211 and 3S3111
4S2211 and 3S3111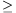 2S2211. Thus
2S2211. Thus
2S33+6S321+12S3111=2S33+2.S321+4.S321+4.3S3111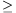
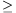 3S222+2.6S222+4.4S2211+4.2S2211=15S222+24S2211.
3S222+2.6S222+4.4S2211+4.2S2211=15S222+24S2211.
Solution 2. The polynomial f(x)=(x-a)(x-b)(x-c)(x-d) has four positive (not necessariliy different) roots. Thus, its derivative has three positive roots; denote them by u, v and w.
By Viete's formulae,
f'(x)=4x3-3(a+b+c+d)x2+
+2(ab+ac+ad+bc+bd+cd)x-(abc+abd+acd+bcd)=
=4(x3-(u+v+w)x2+(uv+uw+vw)x-uvw).
Thus
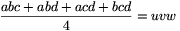
and
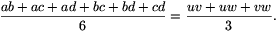
Substituting these in (1), it becomes the inequality between the arithmetic and geometric means of uv, uw and vw.
A. 271. Prove that for any prime, p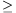 5, the number
5, the number
| (1) | 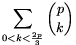 |
is divisible by p2.
Vojtech Jarnik Mathematics Competition, Ostrava, 2001
Solution. Each term of (1) is divisible by p, so our goal is to prove that
| (2) |  |
is divisible by p.
For an arbitrary integer 1 x<p, let x-1 be the multiplicative inverse of x modulo p.
x<p, let x-1 be the multiplicative inverse of x modulo p.
For all 0<k<p,
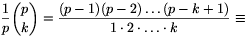
 (-1).(-2).....(-k+1).1-1.2-1.....k-1
(-1).(-2).....(-k+1).1-1.2-1.....k-1 (-1)k.k-1 (mod p),
(-1)k.k-1 (mod p),
and