A 2001. októberi A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 272. A Bergengóc Országgyűlés 100 képviselője a Parlament nagytermének 10 padsorában 10 oszlopban foglal helyet. A küldötteknek mind különböző a fizetése. Minden képviselő megkérdezi szomszédait (a maga mellett, előtt és mögött ülőket, összesen tehát legfeljebb 4-et), hogy mennyi a fizetésük. A küldöttek meglehetősen irigyek: csak azok elégedettek a bérükkel, akiknek legfeljebb egy olyan szomszédja van, aki többet keres náluk. Legfeljebb hány olyan képviselő lehet a Parlamentben, aki meg van elégedve a fizetésével?

A Kvant nyomán

Megoldás. Megmutatjuk, hogy legfeljebb 72 elégedett képviselő lehet. Ábrázoljuk a képviselőket egy 10x10 pontból álló négyzetráccsal, és mindegyik rácspont mellé írjuk oda a megfelelő képviselő fizetését. A szomszédos rácspontok közé pedig rajzoljunk nyilakat úgy, hogy minden nyíl a kisebbik számtól a nagyobbik felé mutasson:

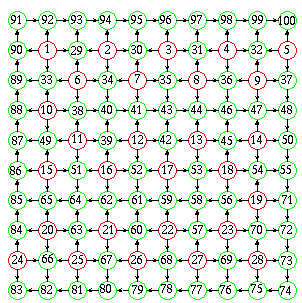
(Zölddel jelöltük az elégedett, pirossal az elégedetlen képviselőket.)

Legyen a a sarkokban ülő elégedett képviselők száma, b az oldalak mentén ülőké, c pedig azoké, akik belül ülnek.

A nyilak száma 180. Az elégedett képviselőktől legfeljebb egy-egy nyíl indul ki. Lesz olyan is, akitől nem indul ki nyíl, például a legnagyobb fizetésű (nyilván elégedett) képviselőtől. Ezért az elégedett képviselőktől kiinduló nyilak száma legfeljebb a+b+c-1.

A sarkokban ülő 4-a elégedetlen képviselőtől legfeljebb (4-a)^.2 nyíl indul ki. Az oldalak mentén ülő 32-b elégedetlen képviselőtől legfeljebb (32-b)^.3, a belül ülő (64-c) elégedetlen képviselőtől pedig legfeljebb (64-c)^.4. A nyilak számát összeszámolva,

180(a+b+c-1)+(4-a)^.2+(32-b)^.3+(64-c)^.4,

vagyis

a+2b+3c179.

Az oldalak mentén ülő 36 képviselő közül a legkisebb fizetésű biztosan nem elégedett, ezért a+b35. Ezen kívül triviálisan a4. Az egyenlőtlenségeket összeadva,

3(a+b+c)=(a+2b+3c)+(a+b)+a179+35+4=218,

vagyis a+b+c72. Az elégedett képviselők száma tehát nem lehet 72-nél nagyobb.

Az ábrán látható esetben éppen 72 elégedett képviselő van.

A. 273. Szerkesszük meg az ABC háromszöget, amelynek beírt köre az AB, BC, CA oldalakat rendre a C₁, A₁, B₁ pontokban érinti, ha adott az A csúcs, az A₁B₁ egyenes és a B₁C₁ szakasz felezőpontját a B csúccsal összekötő egyenes.

Javasolta: Kálmán Tamás, Budapest

Megoldás. Legyenek a háromszög szögei , és , a beírt kör középpontja O, a B₁C₁ szakasz felezőpontja F, a BF és az A₁B₁ egyenesek metszéspontja M, az A₁B₁ egyenes és az AF szögfelező metszéspontja pedig N. Először bebizonyítjuk, hogy az M pont az A-ból induló külső szögfelezőn van, illetve, ami ezzel ekvivalens, hogy az AM és B₁C₁ szakaszok párhuzamosak.

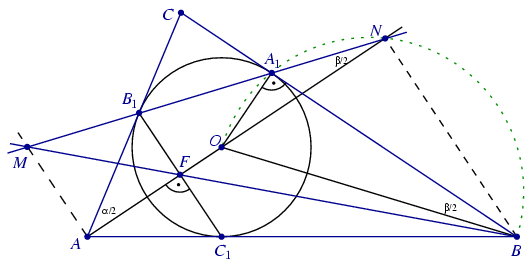
Az A₁B₁C és AB₁N háromszögek szögeit kiszámítva kapjuk, hogy ANB₁=/2. Mivel ez megegyezik az OBA₁ szöggel, az OBNA₁ négyszög húrnégyszög és BNO=BA₁O=90^o. Mivel a C₁FA szög is ugyanekkora, a BN és B₁C₁ szakaszok párhuzamosak.

A párhuzamos szelők tételéből AF:AN=C₁F:BN=FB₁:BN=MF:MB, ebből pedig következik, hogy AM és BN is párhuzamos.

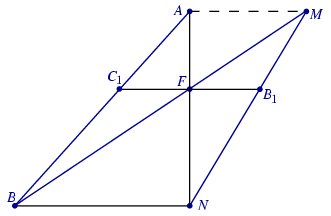
Ezek ismeretében a szerkesztési lépések:

1. Megszerkesztjük az A₁B₁ és BF egyenesek metszéspontját, az M pontot.

2. Merőlegest állítunk az A ponrban az AM egyenesre. Ez a háromszög belső szögfelezője, amely a megadottt A₁B₁ és BF egyenesekből kimetszi az N, illetve F pontokat.

3. Az N pontban merőlegest állítunk az AN egyenesre. Ez a BF egyenesből kimetszi B-t.

4. Az F pontban AF-re állított merőleges és az A₁B₁ egyenes metszéspontjaként megkapjuk B₁-et.

5. A B₁ pontban merőlegest állítunk az AB₁ egyenesre; ez az AF egyenest O-ban metszi.

6. Az AB egyenest tükrözve a BO szögfelezőre, megkapjuk a BC oldalegyenest. A BC oldalegyenes és AB₁ metszéspontjaként megkapjuk a C csúcsot is.

A. 274. Legyenek a, b, c olyan pozitív egészek, amelyekre ac=b²+b+1. Bizonyítsuk be, hogy az

egyenletnek létezik egész megoldása.

Lengyel versenyfeladat

1. megoldás. A feladat állítását b szerinti teljes indukcióval igazoljuk. Megengedjük a b=0 esetet is; ilyenkor csak a=c=1 lehetséges, és x=y=1 egy megoldás.

Tegyük most fel, hogy b pozitív, és az állítás b minden kisebb értéke esetén igaz. Az a és c számok nem lehetnek egyszerre b-nél nagyobbak, mert a,cb+1 esetén ac(b+1)²>b²+b+1. Mivel az a és c számok felcserélésére az állítás szimmetrikus, az általánosság csorbulása nélkül feltehetjük, hogy ab.

Legyen A=a, B=b-a, C=a-2b+c-1. Ezek egész számok, és teljesül rájuk, hogy

B²+B+1=(b-a)²+(b-a)+1=

=(b²+b+1)-2ab+a²-a=

=ac-2ab+a²-a=a(a-2b+c-1)=AC,

továbbá A>0, 0B<b, és C=(B²+B+1)/A>0. Az indukciós feltevés tehát alkalmazható az A, B, C számokra: eszerint léteznek olyan X és Y egész számok, amelyekre

AX²-(2B+1)XY+CY²=1.

Behelyettesítve A, B és C definícióját,

1=AX²-(2B+1)XY+CY²=

=aX²-(2b-2a+1)XY+(a-2b+c-1)Y²=

=a(X+Y)²-(2b+1)(X+Y)Y+cY².

Ez pedig azt jelenti, hogy az x=X-Y, y=Y számpár megoldása az (1) egyenletnek.

2. megoldás. Tekintsük a síkbeli derékszögű koordináta-rendszerben azokat az (x,y) pontokat, amelyekre ax²-(2b+1)xy+cy²<2. Némi számolással ellenőrizhető, hogy ezek egy ellipszislemezt alkotnak, amelynek területe \(\displaystyle {4\pi\over\sqrt3}\) egység.

Az ellipszislemez szimmetrikus az origóra és konvex, területe nagyobb, mint 4 egység. Ezért a Minkowski-tétel szerint tartalmaz az origón kívül más rácspontot is. Ebben a rácspontban ax²-(2b+1)xy+cy² értéke 0 és 2 közé esik, vagyis 1.

Megjegyzés. Az 1. megoldásban valójában az ellipszislemezt az (x,y)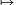(x-y,y) transzformációval egy másik, ugyanakkora területű ellipszisbe képezzük, amelynek együtthatói kisebbek. A transzformációt többször megismételve végül mindig az x²-xy+y²<2 ellipszislemezt kapjuk. Ez az ellipszis az origón kívül további hat rácspontot tartalmaz: a (1,0), a (0,1) és a (1,1) pontokat. Ennek megfelelően az egyenletnek minden esetben hat egész számpár megoldása.