A 2001. októberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 640.  A Gergely naptár szerint 400 egymást követő év során összesen 97 szökőnapot kell beiktatni. Hány év elteltével lesz 1 nap eltérés a Gergely naptár és a ,,pontos'' naptár között, ha egy év hossza 365 nap 5 óra 48 perc 46 másodperc?

Megoldás. A kerek évektől eltekintve a Gergely naptár 400 évente 97 napot (azaz 97^.24=2328 órát) kínál fel az 5 óra 48 perc 46 másodperc 400-szorosával szemben. A perceket célszerű 4/5 órának számolni; így ebből és az órákból 400 év alatt 2320 óra, vagyis 8 órával kevesebb adódik, mint 97 nap. A Gergely naptár javára tehát 8 óra, vagyis 28800 másodperc áll szemben a 400^.46=18400 másodperccel. Ezért a többlet 400 évenként 10400 másodperc. Ahhoz, hogy ebből egy teljes nap (vagyis 86400 másodperc) összejöjjön (400^.86400)/10400$\displaystyle sim$3323 évre van szükség.

C. 641.  Egy téglalap alakú papírlapot az átlója mentén összehajtunk. A dupla rétegen túlnyúló részeket levágva, a megmaradt papír széthajtás után rombusz alakú lesz. Ezt most a középvonala mentén hajtjuk össze, és a papírt az előbbihez hasonlóan megint körbenyírjuk. Milyen téglalapból induljunk ki, hogy a végül megmaradt papír széthajtás után szabályos hatszög alakú legyen?

Megoldás.

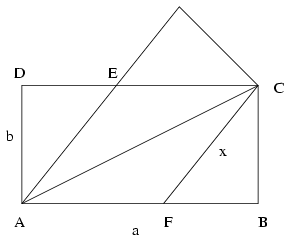
Az ABCD téglalapban AB=a, AD=b, a rombusz oldalát jelölje x.

Az ADE derékszögű háromszögben x²=b²+(a-x)², innen
(1):$\displaystyle x={a^2+b^2\over2a}$.

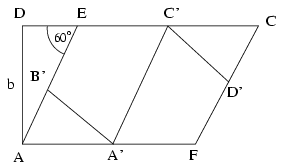
A rombuszt a középvonala mentén összehajtva az A'B'EC'D'F szabályos hatszöget kapjuk, C'EB'$\displaystyle angle$=120^o, ezért az ADE derékszögű háromszögben AED$\displaystyle angle$=60^o és $\displaystyle {b\over x}=\sin60^{\circ}$-ból
(2): $\displaystyle x={2\sqrt3\over3}b$.

(1)-ből és (2)-ből

$\displaystyle {2\sqrt3\over3}b={a^2+b^2\over2a}.$

Az egyenletet rendezve és megoldva kapjuk, hogy $\displaystyle a=\sqrt3b$. Ennek az aránynak kell teljesülnie a téglalap oldalaira. Könnyen ellenőrizhető, hogy a kapott hatszög szabályos.

C. 642.  Egy természetes szám négyzetének utolsó két jegyét felcserélve az eggyel nagyobb szám négyzetét kapjuk. Határozzuk meg az összes ilyen számot.

Javasolta: Fried Ervin, Budapest

Megoldás. Ha n² utolsó két jegye A és B (ebben a sorrendben), akkor (n+1)² utolsó két jegye sorrendben B és A. Így:

2n+1=(n+1)²-n²=(10B+A)-(10A+B)=9(B-A).

Ebből azonnal kapjuk, hogy B-A páratlan. A=0 lehetetlen, mert 0-ra végződő négyzetszám két utolsó jegye 0, ezért B=0 is teljesül; és 2n+1 nem lehet 0. Ez azt is jelenti, hogy B>A. Tekintettel arra, hogy B$\displaystyle le$9, ezért B-A$\displaystyle le$9-1=8. Mivel B=A páratlan, ezért B-A$\displaystyle in${1,3,5,7}. Eszerint n$\displaystyle in${4,13,22,31}. A megfelelő párok négyzetei: 16 és 25; 169 és 196; 484 és 529; 961 és 1024. Ezek közül csak egy felel meg a kirótt feltételnek: 13.

C. 643.  Az ABC háromszög területe t, kerülete k, a körülírt kör sugara R. Bizonyítsuk be, hogy $\displaystyle 4tR\le\left({k\over3}\right)^3$.

Megoldás. Az ABC háromszög oldalait és szögeit a szokásos módon jelölve felírhatjuk, hogy $\displaystyle t={ab\sin\gamma\over2}$, $\displaystyle R={c\over2\sin\gamma}$ és k=a+b+c. Helyettesítve az egyenlőtlenségbe és elvégezve az egyszerűsítéseket: $\displaystyle abc\leq\left({a+b+c\over3}\right)^3$ egyenlőtlenséghez jutunk. Ez pedig nyilván teljesül, mivel a, b, c pozitív így számtani közepük mindig nagyobb vagy egyenlő, mint a mértani közepük. Egyenlőség csak szabályos háromszög esetén áll fenn.

C. 644.  Egy háromszög szögei , és . Bizonyítsuk be, hogy:

$\displaystyle {\cos\alpha\over\sin\beta\sin\gamma}+{\cos\beta\over\sin\alpha\sin\gamma}+{\cos\gamma\over\sin\alpha\sin\beta}=2.$

Javasolta: José Luis Díaz, Barcelona

Megoldás. A bizonyítandó azonosság:

$\displaystyle {\cos\alpha\over\sin\beta\sin\gamma}+{\cos\beta\over\sin\alpha\sin\gamma}+{\cos\gamma\over\sin\alpha\sin\beta}=2.$

A 0-tól különböző 2sin$\displaystyle alpha$sin$\displaystyle beta$sin$\displaystyle gamma$-val végigszorozva és a kétszeres szög szinuszára vonatkozó azonosságot $\displaystyle alpha$ és $\displaystyle beta$ esetében felhasználva azt nyerjük, hogy
(1): sin2$\displaystyle alpha$+sin2$\displaystyle beta$+2sin$\displaystyle gamma$cos$\displaystyle gamma$=4sin$\displaystyle alpha$sin$\displaystyle beta$sin$\displaystyle gamma$.

A bal oldalon levő első két tag összege sin2$\displaystyle alpha$+sin2$\displaystyle beta$=2sin($\displaystyle alpha$+$\displaystyle beta$)cos($\displaystyle alpha$-$\displaystyle beta$).

Az $\displaystyle alpha$+$\displaystyle beta$+$\displaystyle gamma$=180^o összefüggést felhasználva kapjuk, hogy (1) bal oldalán
(2): 2sin$\displaystyle gamma$(cos($\displaystyle alpha$-$\displaystyle beta$)+cos$\displaystyle gamma$)=2sin$\displaystyle gamma$(cos($\displaystyle alpha$-$\displaystyle beta$)-cos($\displaystyle alpha$+$\displaystyle beta$))

áll. Itt a zárójelben szereplő összegre

cos($\displaystyle alpha$-$\displaystyle beta$)-cos($\displaystyle alpha$+$\displaystyle beta$)=-2sin$\displaystyle alpha$sin(-$\displaystyle beta$)=2sin$\displaystyle alpha$sin$\displaystyle beta$

adódik, tehát (2) valóban megegyezik (1) jobb oldalával.