A 2001. novemberi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3466. Domború tükörbe nézve az orrunk aránytalanul nagyobbnak látszik, mint a fülünk. Miért? (3 pont)

Tarján Imre fizikaverseny, Szolnok

Megoldás. A leképezési törvény alapján domború tükör esetén a ,,nagyítás''

$\displaystyle {K\over T}={{\vert k\vert}\over t}={{\vert f\vert}\over t+\vert f\vert}.$

Eszerint

$\displaystyle {(K_1/T_1)\over(K_2/T_2)}={t_2+\vert f\vert\over t_1+\vert f\vert}.$

Mivel fülünknek a tükörtől mért távolsága (t₂) nagyobb, mint az orrunké (t₁), a képen az orrunk a fülünkhöz képest nagyobb, mint a valóságos arányuk:

$\displaystyle {K_1\over K_2${T_1\over T_2}.">

P. 3467. Pihenés nélkül kerékpározva két város között oda-vissza 6 óra a menetidő. Milyen messze van a két város egymástól, ha a vízszintes útszakaszokon 16 km/h, lejtőn felfelé 12 km/h, lejtőn lefelé pedig 24 km/h átlagsebességgel haladunk? (3 pont)

Közli: Kotormán Mihály, Debrecen

Megoldás. A feladat általános megoldásához kevés az adat, de a jelen sebességértékek mellett megoldható: a két város távolsága 48 km.

A megoldhatóság azon múlik, hogy a felfelé, illetve lefelé haladás sebességének ,,harmonikus közepe'' éppen megegyezik a vízszintes útszakaszhoz tartozó átlagsebességgel. Emiatt lényegtelen, hogy az út mekkora hányada emelkedik és mekkora a vízszintes szakasz.

P. 3468. Hőszigetelt edényben 15 ^oC-os csapvíz van. Ebbe tesszük a mélyhűtőből kivett -15 ^oC-os jégkockákat. Lehet, hogy nem történik halmazállapotváltozás? Mikor olvad meg a jég egy része? Mikor olvad meg az összes jég? Mikor fagy meg az összes víz? (4 pont)

Közli: Szegedi Ervin, Debrecen

Megoldás. Jelölje a jég és víz tömegarányát r!

Ha r<0,17, az összes jég felolvad, és a közös hőmérséklet (Celsius-skálán mérve) pozitív lesz.

Ha 0,17<r<2, a közös hőmérséklet 0 ^oC, és a jég egy része megmarad.

Amennyiben 2<r<12,7, a közös hőmérséklet megint 0 ^oC, de most a víz egy része kifagy.

Végül ha 12,7<r, az összes víz megfagy, és a közös hőmérséklet negatív lesz.

P. 3469. Az ábrán látható T alakú merev test három egyforma rúdból áll, és a rudak csatlakozási pontjában a síkjukra merőleges vízszintes tengely körül elfordulhat. A jobb oldali rúd végén és a rudat 2:3 arányban osztó pontban rögzített kötelek egy-egy vízszintes, ékkel alátámasztott rudat tartanak. A felső rudat tartó ék az alsó rudat 3:2 arányban osztja. A felső rúd tömege m₁, az alsóé m₂, a felső rúdra helyezett test tömege pedig m₃. Mekkora tömegű testet kell a bal oldali rúd végén felfüggeszteni az egyensúly biztosításához? Adatok: m₁=2,5 kg, m₂=6,0 kg, m₃=7,5 kg.

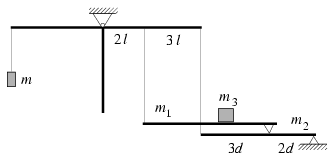
(5 pont)

Közli: Piacsek István, Sopron

Megoldás. $\displaystyle m={2\over5}(m_3+m_1)+{1\over2}m_2=7{,}0$ kg. Az eredmény független az m₃ tömegű test helyzetétől; ez a ,,mázsás mérleg'' működésének alapja.

P. 3470. Egy lejtő végéhez az ábrán látható módon egy kiskocsi csatlakozik. A lejtőről h magasságból elengedett test a könnyen gördülő kiskocsi közepéig csúszik. (A lejtő és a test közötti súrlódás, valamint a kiskocsi kerekeinek tömege elhanyagolható.) Milyen magasból indítsuk a testet, hogy éppen a kiskocsi végénél álljon meg?

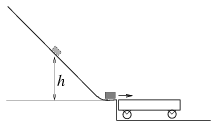
(4 pont)

Közli: Kiss Miklós, Gyöngyös

Megoldás. Kérdezzünk így: a kiskocsin mekkora s utat fut be a lejtőről H magasságból indított test? Ebben a problémában egyetlen hosszúság dimenziójú bemenő adat van, a H magasság, és a feladat szempontjából lényeges gravitációs állandó dimenziójából sem ,,keverhető ki'' hosszúság, így az ugyancsak hosszúság dimenziójú s-nek arányosnak kell lennie H-val: s/H=konstans.

Eszerint a kérdéses magasság éppen 2h.

(Részletesen végigszámolva a feladatot

$\displaystyle s={1\over\mu}{M\over m+M}H$

adódik, ahol $\displaystyle mu$ a test és a kiskocsi közötti súrlódási együttható, m és M pedig a test és a kiskocsi tömege.)

P. 3471. Vékony, de elég merev huzalt 0,6 m sugarú, 30^o meredekségű csavarvonal alakra hajlítunk, és úgy rögzítjük, hogy a csavarvonal tengelye függőleges legyen. Ezután a huzalra egy apró, átfúrt gyöngyöt fűzünk, amit egy adott pillanatban elengedünk. Mekkora sebességre gyorsul fel a gyöngy, ha a súrlódási együttható 0,5? (5 pont)

Közli: Szkladányi András, Baja (Mikola-verseny döntője, Sopron)

Megoldásvázlat. A gyöngyre a következők erők hatnak:

függőlegesen lefelé az mg nehézségi erő,

a csavarvonal érintőjének irányában (a mozgás irányával ellentétesen) valamekkora S súrlódási erő, továbbá

az érintőre merőleges síkban valamilyen irányú és valamekkora N nagyságú nyomóerő. Ez utóbbi felbontható a csavarvonal szimmetriatengelye felé irányuló N₁ nagyságú, valamint arra merőleges (tehát a csavarvonalat magába foglaló henger függőleges érintősíkjában fekvő, a csavarvonal érintőjére merőleges) N₂ nagyságú komponensekre.

A teljes nyomóerő

$\displaystyle N=\sqrt{N_1^2+N_2^2},$

a súrlódási erő pedig

$\displaystyle S=\mu N=\mu\sqrt{N_1^2+N_2^2}.$

Ha a gyöngy állandósult v sebességgel mozog, akkor a gyorsulásvektora a csavarvonal szimmetriatengelye felé mutat, és a nagysága (mivel a gyöngyszem mozgásának vízszintes vetülete r sugarú és vcos$\displaystyle alpha$ kerületi sebességű egyenletes körmozgás) a=(v²/r)cos² $alpha$ . Az ennek megfelelő mozgásegyenlet:

$\displaystyle N_1=m{v^2\over r}\cos^2\alpha.$

A gyorsulás másik két komponense nulla, ahonnan

N₂-mgcos $alpha$ =0,

S-mgsin$\displaystyle alpha$=0.

A fenti összefüggésekből következik

$\displaystyle mg\sin\alpha=\mu\sqrt{(mg\cos\alpha)^2+\left({mv^2\cos^2\alpha\over r}\right)^2},$

azaz

$\displaystyle v=\sqrt{{rg\over\mu\cos\alpha}\sqrt{{\rm tg}^2\alpha-\mu^2}}\approx2~{\rm m\over\rm s}.$

P. 3472. Egy hasábot és egy rugót egymáshoz erősítünk. A rugó végénél felfüggesztve a hasáb 1 másodperces rezgésidővel rezeg. Ezután a hasábot vízszintes asztalra tesszük, és egy függőleges fal felé lökjük úgy, hogy a rugó ütközőként elöl haladjon. A fallal ütközve a rugó összenyomódik, majd visszalöki a testet, amely éppen akkor áll meg, amikor a rugó teljesen nyújtatlanná válik. Mennyi idő telt el a rugó falhoz érésétől a visszalökött test megállásáig? (4 pont)

Közli: Honyek Gyula, Budapest

Megoldás. Amíg a rugó x szakasznyit összenyomódik, a mozgásegyenlet

ma=-Dx-$\displaystyle mu$mg,

melynek megoldása (mint az a gyorsulásmentes esetnek megfelelő x₀=$\displaystyle mu$mg/D ponttól mért elmozdulásra felírható mozgásegyenletből jól látszik)

$\displaystyle x_1(t)=A_1\sin(\omega t+\varphi_1)-{\mu mg\over D}.$

Amikor a rugó kirúgja magát, a mozgásegyenlet

ma=-Dx+$\displaystyle mu$mg,

és ennek megoldása

$\displaystyle x_2(t)=A_2\sin(\omega t+\varphi_2)+{\mu mg\over D}.$

A két x(t) függvény abban a $tau$ időpontban illeszkedik egymáshoz, amikor a sebesség 0, azaz

$\displaystyle \omega\tau+\varphi_1=\omega\tau+\varphi_2={\pi\over2}$, és 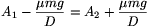$A_1-{\mu mg\over D}=A_2+{\mu mg\over D}$ .

Amikor a test újra megáll, vagyis a $\displaystyle tau$+T/2 időpontban x újra 0, azaz A₂=$\displaystyle mu$mg/D. Ezekből $\displaystyle varphi$₁= $varphi$ ₂=$\displaystyle varphi$, A₁=3 $mu$ mg/D, sin$\displaystyle varphi$=1/3 (hiszen x₁(0)=0), továbbá $tau$ =( $pi$ /2- $varphi$ )/ $omega$ . A kérdéses $\displaystyle Delta$t=$\displaystyle tau$+T/2 időtartam tehát

$\displaystyle \Delta t=T\left({3\over4}-{{\rm arcsin}(1/3)\over2\pi}\right)=0{,}7T.$

Mivel a T rezgési periódusidő ugyanakkora, mint a felfüggesztett test esetében, $\displaystyle Delta$t=0,7 s.

P. 3473. Milyen tömegszázalékos összetételű az a hidrogén-hélium gázelegy, amelynek izobár tágulásakor a környezettől felvett hő 70 %-a a belső energiát növeli? (4 pont)

Közli: Kopcsa József, Debrecen (Mikola Sándor fizikaverseny)

Megoldás. Egy adott mennyiségű gázban legyen a He és a H móljainak száma rendre n₁ és n₂. A környezetből felvett hő, illetve a belső energia változása 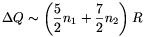$\Delta Q\sim\left({5\over2}n_1+{7\over2}n_2\right)R$

és $\displaystyle \Delta E\sim\left({3\over2}n_1+{5\over2}n_2\right)R$.

A kettő aránya akkor 0,7, ha n₂=5n₁. Felhasználva, hogy a móltömegek aránya 2:1, a tömegszázalékos összetétel

$\displaystyle x_1=2{n_1\over2n_1+n_2}=0{,}286=28{,}6\%$, $\displaystyle x_2={n_2\over2n_1+n_2}=0{,}741=71{,}4\%$.

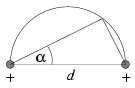
P. 3474. Egy d hosszúságú szakasz végpontjaiban azonos nagyságú pozitív ponttöltések vannak. Mekkora az elektromos térerősség nagyságának és az elektromos potenciálnak a hányadosa a szakasz fölé emelt Thalész-kör egy $alpha$ szöggel jellemzett pontjában?

(4 pont)

Közli: Légrádi Imre, Sopron

Megoldás.

$\displaystyle {\vert E\vert\over U}={1\over d}{\sqrt{\sin^4\alpha+\cos^4\alpha}\over\sin\alpha\cos\alpha(\sin\alpha+\cos\alpha)}.$

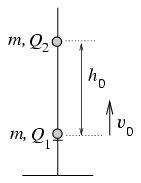
P. 3475. Az ábrán látható vékony, függőleges szigetelő rúd alsó végén levő ütközőn egy m=10^-4 kg tömegű, Q₁ töltésű gyöngy nyugszik. Felette h₀=20 cm távolságban egy ugyancsak m tömegű, Q₂ töltésű gyöngy lebeg. Egy adott pillanatban az alsó gyöngyöt megpöcköljük, ez ekkor v₀=2 m/s sebességgel elindul felfelé. Legfeljebb mennyire közelíti meg az első gyöngy a felsőt? (A gyöngyök súrlódásmentesen csúszhatnak a rúdon.)

(6 pont)

Közli: Kiss László, Budapest (Egyetemi felvételi feladat alapján)

Megoldás. A rendszer mozgása során a tömegközéppont úgy mozog mint egy (2m tömegű) h₀/2 magasban v₀/2 sebességgel függőlegesen felfelé hajított tömegpont, a két test pedig ehhez a ponthoz közelít, majd ettől a ponttól távolodik szimmetrikusan, mintha nem lenne gravitáció. Legyenek a pillanatnyi magasságok és sebességek értelemszerűen

$\displaystyle h_{1,2}=h\mp{s\over2}$, $\displaystyle v_{1,2}=v\pm{u\over2}$

és írjuk fel a rendszer energiáját e változókkal:

$\displaystyle {1\over2}mv_1^2+{1\over2}mv_2^2+mgh_1+mgh_2+{mgh_0^2\over h_2-h_1}=(mv^2+2mgh)+\left(m{u^2\over4}+{mgh_0^2\over s}\right).$

Itt kihasználtuk, hogy a kezdeti egyensúly miatt kQ₁Q₂/h₀²=mg. A jobb oldalon az első zárójelben a tömegközéppont mozgásával kapcsolatos energia járulék áll. Mivel ez önmagában is állandó, a második zárójelben álló, a tömegpontok relatív mozgásával kapcsolatos energia is megmaradó mennyiség. Kezdetben s=h₀ és u=v₀, tehát

$\displaystyle m{u^2\over4}+{mgh_0^2\over s}=m{v_0^2\over4}+{mgh_0}.$

s akkor a legkisebb, ha u=0, innen

$\displaystyle s_{\rm min}={4gh_0^2\over v_0^2+4gh_0}\approx13~\rm cm.$

Megjegyzés: A megoldás során feltételeztük, hogy a vizsgált mozgás során az alsó gyöngy még nem csapódik neki az ütközőnek. Ez jogos (bár csak integrálszámítás felhasználásával igazolható) feltevés.

P. 3476. Homogén mágneses térben körpályán kering egy elektron. Lehet-e nagyobb az elektron mozgása által keltett mágneses indukcióvektor értéke a kör középpontjában, mint a homogén mágneses teret jellemző indukcióvektor? (5 pont)

Közli: Varga István, Békéscsaba (Bay Zoltán fizikaverseny, Sarkad)

Megoldás. Egy köráram középpontjában az áram által keltett indukció

$\displaystyle B_i={\mu_0\over2}{I\over R}.$

Amikor egy elektron v sebességgel R sugarú körpályán kering, az áramerősség

$\displaystyle I={ev\over2\pi R}.$

Ha a v sebességgel mozgó elektront B₀ indukciójú mágneses mező tartja a körpályán, a mozgásegyenlet:

$\displaystyle evB={mv^2\over R}.$

Ezeket egybevetve

$\displaystyle {B_i\over B_0}={\mu_0\over4\pi}{e^2\over mR},$

amelyet a $\displaystyle mu$₀$\displaystyle varepsilon$₀=1/c² (c a vákuumbeli fénysebesség) felhasználásával

$\displaystyle {B_i\over B_0}=\left[{e^2\over4\pi\varepsilon_0}{1\over mc^2}\right]\cdot{1\over R}$

alakba is írhatunk.

A keringő elektron mozgása által keltett mágneses mező a fenti képlet szerint akkor lehetne nagyobb, mint a homogén B₀, ha R kisebb lenne a szögletes zárójelben szereplő, klasszikus elektronsugárnak nevezett mennyiségnél. Ennek számértéke azonban r₀=2,8^.10^-15 m, nagyságrendileg az atommag méretével megegyező távolság. Az elektron - a klasszikus fizika törvényei szerint - nem lehet kisebb méretű, mint r₀, hiszen ellenkező esetben a saját elektrosztatikus energiája elérné, vagy meghaladná a teljes E=mc² nyugalmi energiáját. Azt is mondhatjuk, hogy a klasszikus elektrodinamika érvényét veszti, ha r₀-nál kisebb méretekben lezajló eseményekre, folyamatokra akarnánk alkalmazni. (Egyéb okok, pl. az elektron hullámtermészete miatt már sokkal nagyobb méreteknél is alkalmazhatatlan a klasszikus elmélet.) A feltett kérdésre tehát a válasz nemleges: az elektron nem hozhat létre nagyobb mágneses teret a körpálya középpontjában, mint amekkora mágneses tér az elektront körpályán tartja.

P. 3477. Homogén, vékony lécből a, b és c oldalélű háromszög alakú keretet állítunk össze. A léckeret össztömege m. Mekkora a keret tehetetlenségi nyomatéka a tömegközéppontján átmenő, a háromszög síkjára merőleges tengelyre vonatkozóan? (5 pont)

Közli: Gnädig Péter, Budapest

Megoldás.

$\displaystyle \Theta_{\rm keret}={m\over12(a+b+c)}\left(a^3+b^3+c^3+3abc\right).$

Már regisztráltál?
Új vendég vagy?