Solutions for advanced problems "A" in December, 2001

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

A. 278. P is a point on the extension of the diagonal AC of rectangle ABCD beyond C, such that BPD$\displaystyle angle$=CBP$\displaystyle angle$. Find the ratio PB:PC.

Solution 1. Let the perpendicular projections of P onto the lines CD and AB be Q and R, respectively, and let PAR$\displaystyle angle$=PCQ$\displaystyle angle$=$\displaystyle alpha$ and BPD$\displaystyle angle$=CBP$\displaystyle angle$=BPR$\displaystyle angle$=$\displaystyle beta$. With the length of segment PC chosen to be 1, let the length of segment PB be x. The task is to determine x.

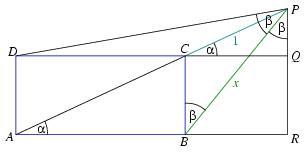
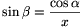From the triangles PCQ and PBR, for example, and the rectangle CBRQ, xsin$\displaystyle beta$=BR=CQ=cos $alpha$ , that is, $\sin\beta={\cos\alpha\over x}$ .

From the triangles PDQ, PCQ, PAR, PBR, and the rectangle ARQD,

$\displaystyle \tan2\beta={DQ\over PQ}={AR\over\sin\alpha}={PR\cdot\cot\alpha\over\sin\alpha}={x\cdot\cos\beta\cdot\cot\alpha\over\sin\alpha}=x\cdot\cos\beta\cdot{\cos\alpha\over\sin^2\alpha}.$

By rearranging and substituting $\displaystyle \sin\beta={\cos\alpha\over x}$, we have

$\displaystyle {x\cdot\cos\alpha\over\sin^2\alpha}={\tan2\beta\over\cos\beta}={2\sin\beta\over1-2\sin^2\beta}={2{\cos\alpha\over x}\over1-2{\cos^2\alpha\over x^2}},$

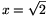x²=2sin² $alpha$ +2cos²$\displaystyle alpha$=2, hence $x=\sqrt2$ .

Thus the ratio PB:PC is always 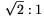$\sqrt2:1$ , independently of the angle $\displaystyle alpha$.

Solution 2. This is an elementary proof for 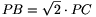$PB=\sqrt2\cdot PC$ . Let S be the intersection of the lines BC and PD. The triangle BPS is isosceles, according to the given information. Let R be the point that is on the same side of line PB as S, and for which the triangle PBR is isosceles and right-angled, that is, BR=PR and PRB$\displaystyle angle$=90^o.

Let, furthermore, T be the intersection of the circumscribed circle of rectangle ABCD with the line PD. BD is a diameter in the circle, therefore the segment BT is perpendicular to the line PD.

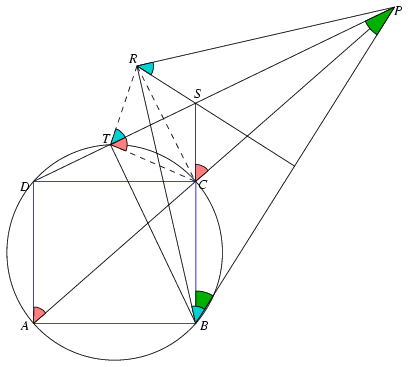
As ACTD is a cyclic quadrilateral, PTC$\displaystyle angle$=PAD$\displaystyle angle$=PCS$\displaystyle angle$. The angles of the triangles PCS and PTC are pairwise equal, thus the two triangles are similar, and PC:PS=PT:PC, that is, PC²=PS^.PT.

As PRB$\displaystyle angle$=PTB$\displaystyle angle$=90^o, the quadrilateral PRTB is also cyclic, and RTP$\displaystyle angle$=RBP$\displaystyle angle$=PRS$\displaystyle angle$. The triangles PRS and PTR are also similar, thus with the above reasoning we have PR²=PS^.PT.

We have obtained that PC²=PR²=PS^.PT, that is, PC=PR, and hence $\displaystyle PB:PC=PB:PR=\sqrt2:1$.

A. 279. Are there such rational functions f and g that (f(x))³+(g(x))³=x?

Solution. We shall prove that no rational functions of either real or complex coefficients satisfy this functional equation.

Assume, to the contrary, that there is a solution. Let the product of the denominators of f(x) and g(x) be the polynomial c(x). Then f(x)=a(x)/c(x) and g(x)=b(x)/c(x), with the appropriate polynomials a and b. By substituting these into (1), we have

(2)	a³(x)+b³(x)=x^.c³(x).

Consider a solution of the equation (2), such that c(x) is not 0, and its degree is a minimum. Let $\displaystyle \varepsilon=\cos{2\pi\over3}+i\sin{2\pi\over3}$ be the first third root of unity. The left-hand side of (2) can be factorized:

(3)	(a(x)+b(x))^.(a(x)+$\displaystyle varepsilon$b(x))^.(a(x)+$\displaystyle varepsilon$²b(x))=x^.c³(x).

We state that the three factors on the left-hand side are pairwise relative primes. We shall prove it for the first two factors, the proof is similar for the other pairs. Assume that the polynomials a(x)+b(x) and a(x)+$\displaystyle varepsilon$b(x) have a common factor of at least degree one: d(x). Then d(x) is also a factor of the polynomial $\displaystyle {1\over1-\varepsilon}\big((a(x)+b(x))-(a(x)+\varepsilon b(x))\big)=b(x)$, and similarly, also a factor of a(x). d³(x) is a factor of the left-hand side of (2), and therefore it also divides x^.c³(x), that is, d(x) is a factor of c(x). But then by dividing the polynomials a(x), b(x), c(x) by d(x), we get a solution in which the degree of c is smaller. Therefore, the polynomials a(x)+b(x) and a(x)+$\displaystyle varepsilon$b(x) cannot have a common factor of at least degree one, that is, they are relative primes.

The product of three polynomials that are pairwise relative primes can only have the form x^.c³(x) if two of them are perfect cubes, and one is x times a perfect cube. As the equation is symmetrical in the polynomials b(x), $\displaystyle varepsilon$b(x), $\displaystyle varepsilon$²b(x), we can assume that the first factor is x times a perfect cube, that is, with appropriate polynomials u(x), v(x), w(x),

a(x)+b(x)=x^.u³(x),

a(x)+$\displaystyle varepsilon$b(x)=v³(x),

a(x)+$\displaystyle varepsilon$²b(x)=w³(x),

and

c(x)=u(x)v(x)w(x).

It is easy to show that

(4)	(1+$\displaystyle varepsilon$²)(a(x)+$\displaystyle varepsilon$b(x))+(1+$\displaystyle varepsilon$)(a(x)+$\displaystyle varepsilon$²b(x))=a(x)+b(x).

On the left-hand side, each term is a perfect cube:

(1+$\displaystyle varepsilon$²)(a(x)+$\displaystyle varepsilon$b(x))=d³(x)

and

(1+$\displaystyle varepsilon$)(a(x)+$\displaystyle varepsilon$²b(x))=e³(x)

with appropriate polynomials d(x) and e(x). By substitution of these into (4),

d³(x)+e³(x)=x^.u³(x).

Thus the polynomials d(x), e(x), u(x) represent another solution of the equation. If the degree of u(x) is smaller than the degree of c(x) it is contradiction, as we assumed above that the degree of c(x) was a minimum. On the other hand, the degree of u(x) can only be greater than or equal to the degree of c(x)=u(x)v(x)w(x) if v(x) and w(x) are constants. But then the polynomials a(x) and b(x) are also constant, and thus there is a constant on the left-hand side of (2), while the right-hand side is a polynomial of at least degree one. This is also contradiction.

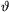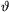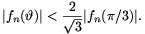
A. 280. For each positive integer n, let f_n($\displaystyle vartheta$)=sin$\displaystyle vartheta$^.sin(2 $vartheta$ )^.sin(4$\displaystyle vartheta$)^....^.sin(2ⁿ $vartheta$ ). For all real $\displaystyle vartheta$ and all n, prove that $|f_n(\vartheta)|<{2\over\sqrt3}|f_n(\pi/3)|.$

IMC 8, Prague, 2001

Solution. Let us allow n=0, too. Then obviously, f₀($\displaystyle vartheta$)=sin$\displaystyle vartheta$.

It is easy to show that on the right-hand side of (5) we have $\displaystyle \left({\sqrt3\over2}\right)^n$, and the statement to prove is:

(6)	$\displaystyle \|f_n(\vartheta)\|<\left({\sqrt3\over2}\right)^n$

The proof is by mathematical induction. In the cases n=1 and n=2, the statement is trivial.

$\displaystyle |\sin\vartheta|<{2\over\sqrt3},$

and

|sin$\displaystyle vartheta$^.sin2$\displaystyle vartheta$|<1.

Now let n>3, and let us assume that the statement is true for all smaller values. If $\displaystyle |\sin\vartheta|\le{\sqrt3\over2}$ then it follows from the assumption that

$\displaystyle |f_n(\vartheta)|=|\sin\vartheta|\cdot|f_{n-1}(2\vartheta)|<{\sqrt3\over2}\cdot\left({\sqrt3\over2}\right)^{n-1}=\left({\sqrt3\over2}\right)^n.$

If $\displaystyle |\sin\vartheta${\sqrt3\over2}|">, then $\displaystyle |\cos\vartheta|<{1\over2}$,

$\displaystyle |\sin\vartheta\cdot\sin2\vartheta|={1\over2}|\cos\vartheta-\cos3\vartheta|<{1\over2}\left({1\over2}+1\right)={3\over4},$

and

$\displaystyle |f_n(\vartheta)|=|\sin\vartheta\cdot\sin2\vartheta|\cdot|f_{n-2}(2\vartheta)|<{3\over4}\cdot\left({\sqrt3\over2}\right)^{n-2}=\left({\sqrt3\over2}\right)^n.$

Already signed up?
New to KöMaL?