A 2001. decemberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 650. Egy képkereskedésben a képek keretének ára egyenesen arányos a bennük lévő festmények értékével. A kereskedő annak érdekében, hogy bizonyos képek ára közötti különbséget csökkentse, felcserél egymással két-két keretet. Az egyik esetben az a kép, amely ötször annyiba került, mint a másik, kereteik felcserélése után már csak háromszor annyiba kerül. Hogyan módosul a ,,Téli táj'' és a ,,Falu rossza'' c. képek árainak aránya, ha kereteik felcserélése előtt a ,,Téli táj'' kilencszer annyiba került, mint a ,,Falu rossza''?

Megoldás. Jelölje az arányossági tényezőt p, azaz egy keret ára a kép árának a p-szerese. A továbbiakban k a keret, K a kép ára, az alsó indexben pedig a képek értelemszerű megkülönböztetése található. Általában tehát k=pK, bármilyen index esetén. A példában szereplő képekre ezek alapján k_e+K_e=5(k_m+K_m), amiből (1+p)K_e=5(1+p)K_m, és így K_e=5K_m; k_e=5k_m. A keretek felcserélése után k_m+K_e=3(k_e+K_m), amiből pK_m+5K_m=3(5pK_m+K_m), így p+5=15p+3, tehát p=1/7. A téli táj és a falu rossza esetében hasonlóan k_t=9k_f, K_t=9K_f, valamint (p+9)K_f=s(9p+1)K_f. Mivel p=1/7, így ebből s=4 adódik. Tehát a keretek felcserélése után a ``Téli táj'' már csak négyszer annyiba kerül, mint a ``Falu rossza''.

C. 651. Az ábrán látható egységnyi területű körben a szürke tartományt félkörívek határolják. Az AB átmérőnek 1/5 egységnyi része esik a satírozott tartomány belsejébe. Mekkora a satírozott tartomány kerülete és a területe?

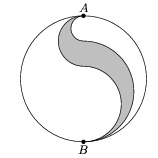
Megoldás. Jelöljük az AB átmérőjű kör sugarát r-rel. Tudjuk, hogy a kör területe egységnyi, azaz 1=r²\(\displaystyle pi\), innen \(\displaystyle r=\sqrt{\frac{1}{\pi}}\). A berajzolt félköröket jelöljük k₁, k₂, k₃, k₄-gyel az 1. ábra szerint.

A k₄ kör átmérője legyen d₄=2x, a k₂ kör átmérője d₂=2y, ekkor k₃ átmérője \(\displaystyle d_3=2x+\frac{2r}{5}\), és \(\displaystyle d_1=2y+\frac{2r}{5}\) a k₁ átmérője.

Először a tartomány kerületét, k-t számítjuk ki, ez a határoló félkörök kerületének összege:

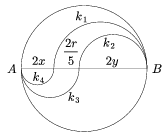
1. ábra

Mivel \(\displaystyle 2x+2y+\frac{2r}{5}\) éppen a kör AB átmérője, a satírozott tartomány kerülete egyenlő a kör kerületével:

\(\displaystyle k=2\pi r=2\pi\frac{\sqrt{\pi}}{\pi}=2\sqrt{\pi}.\)

A satírozott rész T területe egyenlő a k₁ és k₂, valamint a k₃ és k₄ félkörök terület-különbségének az összegével:

\(\displaystyle T=\frac{\pi}{2}\left[\left(x+\frac{r}{5}\right)^2-x^2\right]+\frac{\pi}{2}\left[\left(y+\frac{r}{5}\right)^2-y^2\right]=\frac{\pi}{2}\left[\left(2x+\frac{r}{5}\right)\frac{r}{5}+\left(2y+\frac{r}{5}\right)\frac{r}{5}\right]=\frac{\pi}{2}\frac{r}{5}\left(2x+2y+\frac{2r}{5}\right)\)

Előbb már láttuk, hogy a zárójelben álló összeg éppen 2r, így

\(\displaystyle T=\frac{\pi}{2}\cdot\frac{r}{5}\cdot2r=\frac{1}{5}\)

területegység.

Kirják Erzsébet (Jászberény, Liska József Erősáramú Szki. és Gimn., 11. évf.) dolgozata alapján

C. 652. Legyen s páratlan sok jegyű pozitív egész szám. Jelölje f azt a számot, amely s számjegyeiből áll, csak fordított sorrendben. Bizonyítsuk be, hogy s+f pontosan akkor osztható 11-gyel, ha s is osztható 11-gyel.

Megoldás. Tudjuk, hogy egy szám pontosan akkor osztható 11-gyel, ha a páros és páratlan helyen álló jegyeit összeadva, ezek különbsége osztható 11-gyel.

Először tegyük fel, hogy s osztható 11-gyel. Ekkor, mivel páratlan sok jegyet tartalmaz, ha fordított sorrendben írjuk fel, az eredetileg páratlan helyen álló számjegyek páratlan helyre kerülnek (és ugyanígy a páros helyen álló jegyek párosra). Vagyis az így kapott f szám is osztható lesz 11-gyel, és akkor s+f is.

Ha viszont 11 nem osztója az s-nek, akkor s=11k+m alakban írható, ahol 0<m<11. A  fordított sorrendben felírt f szám 11-gyel osztva ugyancsak m-et ad maradékul. Így s+f=11p+2m, ahol 0<2m<22 és 2m páros, azaz nem osztható 11-gyel.

Ezzel beláttuk a fordított állítást is, vagyis ha s nem osztható 11-gyel, akkor s+f sem osztható.

Varga Anikó (Komarno, Marianum Egyh. Gimn., 9. évf.)

C. 653. A p paraméter hány különböző értékére van az

x²-y²=0

xy+px-py=p²

egyenletrendszernek pontosan egy megoldása?

Megoldás. Az első egyenletből (x+y)(x-y)=0, így a második egyenletet ez alapján két esetre bontjuk.

I. eset y=-x

Ezt behelyettesítve a második egyenletbe, majd rendezve: -x²+2px-p²=-(x-p)²=0.

Ennek bármilyen p esetén csak egy megoldása van, mégpedig x=p, y=-p.

II. eset y=x

Ezt behelyettesítve a második egyenletbe, majd rendezve x²=p². Ennek csak akkor van egy megoldása, ha p=0, ekkor x=y=0.

Az I. és a II. eset csak akkor adja ugyanazt az egy megoldást, ha p=0, tehát az egyenletnek csak ebben az egy esetben van egy megoldása.

C. 654. f_a, f_b és f_c jelölik egy a, b, c oldalú, T területű háromszög belső szögfelezőinek a hosszát. Igazoljuk, hogy

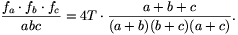
Javasolta: Kovács Gabriella, Budapest

Megoldás. Az ABC háromszög C-ből induló szögfelezője f_c. Fejezzük ki f_c-t a háromszög oldalainak segítségével.

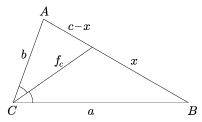
Az f_c szögfelező a C oldalt x és c-x hosszúságú részekre osztja az ábra szerint, a C csúcsnál lévő szög \(\displaystyle gamma\). Mint ismeretes,

\(\displaystyle x=\frac{ac}{a+b},\quad c-x=\frac{bc}{a+b}.\)

Írjuk fel a részháromszögekre a koszinusz tételt:

\(\displaystyle x^2=a^2+f_c^2-2af_c\cos\frac{\gamma}{2},\quad{(c-x)}^2=b^2+f_c^2-2bf_c\cos\frac{\gamma}{2}.\)

A két egyenletből fejezzük ki \(\displaystyle \cos\frac{\gamma}{2}\)-t. A két kifejezés egyenlőségéből egyszerűsítés után kapjuk, hogy

b(a²+f_c²-x²)=a(b²+f_c²-(c-x)²).

Helyettesítsük be az x és c-x előbb kapott értékeit:

\(\displaystyle b\left(a^2+f_c^2-\left(\frac{ac}{a+b}\right)^2\right)=a\left(b^2+f_c^2-\left(\frac{bc}{a+b}\right)^2\right).\)

Innen f_c kifejezhető. A műveletek elvégzése és egyszerűsítés után, valamint felhasználva az \(\displaystyle s=\frac{a+b+c}{2}\) jelölést, kapjuk, hogy

\(\displaystyle f_c=\sqrt{\frac{4ab\cdot s(s-c)}{{(a+b)}^2}}.\)

A betűk ciklikus cseréjével hasonló összefüggést írhatunk fel az f_a és f_b szögfelezőkre is.

Írjuk fel az f_af_bf_c szorzatot:

\(\displaystyle f_af_bf_c=\sqrt{\frac{4ac\cdot s(s-b)\cdot4ab\cdot s(s-c)\cdot4bc\cdot s(s-a)}{{(c+a)}^2\cdot{(b+c)}^2\cdot{(a+b)}^2}}.\)

A számlálóból kiemelhetjük a 8s^.abc-t, a nevező tényezőiből pedig gyököt vonunk, így kapjuk, hogy

\(\displaystyle f_af_bf_c=\frac{2s\cdot abc\cdot4\sqrt{s(s-a)(s-b)(s-c)}}{(a+b)(b+c)(a+c)}.\)

Itt 2s=a+b+c, Héron képlete szerint pedig \(\displaystyle 4\sqrt{s(s-a)(s-b)(s-c)}=4T\), ezeket helyettesítve valóban az (1) összefüggést kapjuk.

Metzing András (Pécs, Leöwey Klára Gimn., 11. évf.)