A 2002. januári számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3488. Adott $\displaystyle alpha$ hajlásszögű lejtőn alapjára állított, tömör, egyenes henger csúszik le. A súrlódási együttható . A henger alaplapján melyik pont tekinthető a lejtő által kifejtett nyomóerő támadáspontjának? (4 pont)

Közli: Rácz György, Mezőkövesd

Megoldás. A lecsúszó hengerre ható S=mgcos súrlódási erőnek a tömegközéppontra vonatkoztatva S^.(h/2) a forgatónyomatéka (h a henger magassága). Ha az N=mgcos$\displaystyle alpha$ nyomóerő támadáspontja a szimmetriatengelytől x távolságra van (a lejtő mentén lefelé), akkor a nyomóerő forgatónyomatéka N^.x.

A henger nem forog, tehát S^.(h/2)=N^.x, azaz fennáll

x=$\displaystyle mu$h/2.

Ez az érték biztosan kisebb, mint a henger sugara, hiszen a csúszás feltétele: $\displaystyle mu$<tg$\displaystyle alpha$=2R/h.

P. 3489. Egy 150 g tömegű hógolyó 20 m/s sebességgel az ablaküveghez csapódik, és 0,01 s alatt megáll. Betörik-e az ablaküveg, ha az üveg a találat helyén legfeljebb 300 N nyomóerőt bír ki? (4 pont)

Közli: Szegedi Ervin, Debrecen

Megoldás. Ha a hógolyó egyenletesen fékeződne le, akkor a rá ható fékezőerő

$\displaystyle F={\Delta(mv)\over t}={0{,}15\cdot20\over0{,}01}=300~\rm N$

lenne, és ugyanekkora nagyságú erőt fejtene ki a hógolyó is az ablakra. Ez éppen a megadott kritikus érték, tehát határeset lenne.

A hógolyó azonban nyilván nem egyenletesen lassul, hanem eleinte kisebb, majd egyre nagyobb erő hatására. Az erő átlagértéke 300 N, tehát kell legyen olyan pillanat, amikor az erő ennél az értéknél nagyobb, - s így az ablak (ha még egy nagyon rövid ideig sem bír ki 300 N-nál nagyobb erőt) betörik.

P. 3490. Hogyan lehet az, hogy egyes helikopterekre kell, másokra nem kell faroklégcsavar? (3 pont)

Lánczos Kornél verseny, Székesfehérvár

Megoldás. A levegő fékezi a helikopter rotorjának forgását, tehát forgatónyomatékot fejt ki a helikopterre. Ha más nyomaték nem hatna, a helikopter teste is (nemkívánatos) forgásba jönne.

A faroklégcsavar szerepe az, hogy az általa kifejtett forgatónyomaték a rotorra ható nyomatékot kiejtse, és így megakadályozza a helikopter testének forgását. Faroklégcsavar nélkül az olyan helikopterek repülhetnek stabilan, amelyek legalább két - egymással ellentétes irányban forgó - rotorral rendelkeznek. Ezek lehetnek közös tengelyen (az egyik a másik felett), de külön tengelyeken is elhelyezkedhetnek (az egyik pl. a gép elején, a másik a hátsó felénél).

P. 3491. Egy villanymotor vonóereje 57,6 km/h sebesség esetén 310 kN. A tápfeszültség 3,6 kV, a nyolc villanymotor tekercseiben 230 A erősségű áram folyik. Határozzuk meg a motor hatásfokát! (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

Megoldás. $\displaystyle eta$=F^.v/(8I^.U)=0,75.

P. 3492. Mekkora annak a mosószeres oldatból formálódott buboréknak a sugara, amelyben a levegő sűrűsége egy ezrelékkel nagyobb, mint a környező levegőé? ($\displaystyle alpha$=0,033 N/m, p₀=10⁵ Pa.) (4 pont)

Közli: Varga István, Békéscsaba

Megoldás. Az R sugarú buborék görbületi nyomása (a buborék külső és belső felületét is figyelembe véve)

$\displaystyle \Delta p={4\alpha\over R},$

és mivel (adott hőmérsékleten) a levegő sűrűsége a nyomásával egyenesen arányos, $\displaystyle Delta$p/p₀=10^-3. Innen

$\displaystyle R={4\alpha\over10^{-3}p_0}=1{,}3~\rm mm.$

P. 3493. Hidrogéngázzal az ábrán látható ABCA körfolyamatot végeztetjük. (p₁=2^.10⁵ Pa, V₁=2 m³, T_A=300 K.)

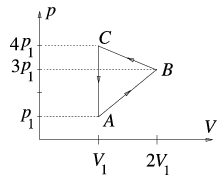
a) Mennyi hőt közlünk a gázzal az egyes részfolyamatokban?

b) Mennyi a gázon végzett összes munka? (4 pont)

Tornyai Sándor verseny, Hódmezővásárhely

Megoldás. a) A hidrogén belső energiája $\displaystyle E={5\over2}pV,$ a gázon végzett munka W=-p$\displaystyle Delta$V, a közölt hő pedig

$\displaystyle Q=\Delta E-W={5\over2}\Delta(pV)+p\Delta V.$

Innen az egyes részfolyamatokban közölt hő:

$\displaystyle Q_{A\rightarrow B}={5\over2}\left(6p_1V_1-p_1V_1\right)+2p_1V_1=14{,}5p_1V_1=5800~\rm kJ,$

$\displaystyle Q_{B\rightarrow C}={5\over2}\left(4p_1V_1-6p_1V_1\right)+3{,}5p_1V_1=-8{,}5p_1V_1=-3400~\rm kJ.$

$\displaystyle Q_{C\rightarrow A}={5\over2}\left(p_1V_1-4p_1V_1\right)=-7{,}5p_1V_1=-3000~\rm kJ.$

A teljes körfolyamat során a gáz

Q=Q_{A$\displaystyle rightarrow$B}+Q_{B$\displaystyle rightarrow$C}+Q_{C$\displaystyle rightarrow$A}=-600 kJ

hőt vesz fel, tehát 600 kJ-t ad le.

b) A gázon végzett munka a p-V diagramon a körfolyamat során körüljárt terület nagysága:

$\displaystyle W={3\over2}p_1V_1=600~\rm kJ.$

Ez az érték természetesen megegyezik a gáz által a körfolyamatban leadott hővel.

P. 3494. A 20 cm sugarú, 8^.10^-7 C töltésű fémgömb körül mekkora annak a képzeletbeli koncentrikus gömbnek a sugara, amely a fémgömb elektrosztatikus terét két egyenlő energiájú tartományra osztja? Mekkora a fémgömb terének összenergiája? (5 pont)

Közli: Holics László, Budapest

Megoldás. Az R sugarú, Q töltésű fémgömb (gömbkondenzátor) elektrosztatikus energiája

$\displaystyle E=k{Q^2\over2R}=14{,}4~\rm mJ.$

Ha a gömb elektrosztatikus terének csak egy R^* sugarú gömbön kívüli részét (r>R^*>R) vizsgáljuk, ennek tere éppen olyan, mint egy R^* sugarú, Q töltésű gömbkondenzátoré, energiája tehát

$\displaystyle E^*=k{Q^2\over2R^*}=E\cdot{R\over R^*}.$

Ez a kifejezés akkor lesz az eredeti E energia fele, ha R^*=2R=40 cm.

P. 3495. Félgömb alakú üveglencse (n=1,5; R=4,8 cm) sík határfelülete matt. A félgömb szimmetriatengelyén pontszerű fényforrás található. A lencsén belépő fénysugarak egy fényes foltot hoznak létre a matt felületen. Hol van a fényforrás, amikor legkisebb a fényfolt? Mennyi ekkor a fényfolt átmérője? (5 pont)

Schwartz emlékverseny, Nagyvárad

Megoldás. A fényes folt r sugarát azok a fénysugarak jelölik ki, melyek éppen súrolják a félgömböt, beesési szögük 90^o. Belátható, hogy az ennél kisebb szögben beeső sugarak a matt felületet az optikai tengelytől r-nél kisebb távolságban érik el.)

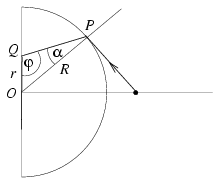
Az $\displaystyle alpha$ törési szöget a Snellius-Descartes-törvény határozza meg:

sin$\displaystyle alpha$=1/n,

ez az érték tehát a fényforrás helyzetétől függetlenül mindig ugyanakkora. Az OPQ háromszögre alkalmazhatjuk a szinusz-tételt:

$\displaystyle r=R\cdot{\sin\alpha\over\sin\varphi}.$

Ez a mennyiség akkor a legkisebb, ha sin$\displaystyle varphi$ a lehető legnagyobb, tehát amikor $\displaystyle varphi$=90^o. A fényes folt sugara ilyenkor

$\displaystyle r=r_{\rm min}={R\over n}=3{,}2~\rm cm,$

és a fényforrás távolsága a félgömb középpontjától

$\displaystyle d={R\over\cos\alpha}=R{n\over\sqrt{n^2-1}}=6{,}4~\rm cm.$

P. 3496. Jelölje $\displaystyle \lambda_{\min}$ a hidrogénatom által kibocsátott fény legrövidebb hullámhosszát! Kibocsáthat-e ez az atom $\displaystyle 2\lambda_{\min}$ hullámhosszúságú fotont? (4 pont)

Nagy László verseny, Kazincbarcika

Megoldás. A legrövidebb hullámhosszú foton a legnagyobb frekvenciájúnak, tehát a legnagyobb energiájúnak felel meg. A hidrogénatom m$\displaystyle rightarrow$n kvantumszámú sugárzási átmeneténél a kibocsátott foton energiája arányos az  $\displaystyle X(m,n)={1\over n^2}-{1\over m^2}$

(m>n)

kifejezéssel, ami akkor a legnagyobb, nevezetesen X_max$\displaystyle approx$1, ha n=1 és m$\displaystyle gg$1.

Egy 2$\displaystyle lambda$_min hullámhosszúságú foton olyan átmenetnek felelne meg, amelyhez

$\displaystyle X(m,n)={X_{\rm max}\over2}={1\over2}$

tartozik. Ez azonban lehetetlen, mert az

$\displaystyle {1\over n^2}-{1\over m^2}={1\over2}$

egyenletnek nincs megoldása a pozitív egész számok között.

A hidrogénatom tehát nem bocsáthat ki 2$\displaystyle lambda$_min hullámhosszúságú fotont.

P. 3497. Egy 1 méter hosszú fonálingát a vízszintesig kitérítünk, majd elengedünk. Mekkora a fonál végén levő test gyorsulásvektorának szögsebessége, amikor a gyorsulásvektor a) függőleges, b) vízszintes helyzetű? (6 pont)

Közli: Sári Péter, Budapest

Megoldás. A fonál $\displaystyle varphi$ szögelfordulása után a fonál szögsebessége

$\displaystyle \omega=\sqrt{{2g\over l}\sin\varphi},$

az ingatest gyorsulásvektorának érintőleges (tangenciális) komponense

a_t=gcos$\displaystyle varphi$,

a sugár irányú (normális) komponense pedig

a_n=-2gsin$\displaystyle varphi$.

A gyorsulásvektor a függőlegessel $\displaystyle gamma$=$\displaystyle varphi$+$\displaystyle psi$ szöget zár be, ahol

$\displaystyle \tg\psi=-{a_n\over a_t}=2\tg\varphi.$

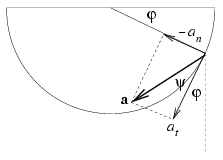
a) A gyorsulásvektor akkor függőleges, amikor =0 (ez =0-nál, vagyis az indítási helyzetben teljesül), illetve akkor, amikor =180^o (ami $\displaystyle varphi$=90^o-nál, azaz a pálya legmélyebb pontján áll fenn).

b) A gyorsulásvektor akkor vízszintes, amikor =90^o, ez $\displaystyle \tg\varphi=1/\sqrt{2}$, azaz =35,3^o-nál következik be.

A gyorsulásvektor $\displaystyle omega$_{$\displaystyle gamma$} szögsebessége a $\displaystyle gamma$ szög időbeli változási sebessége. Mivel $\displaystyle varphi$ változási sebességét, $\displaystyle omega$_{$\displaystyle varphi$}-t $\displaystyle varphi$ függvényében ismerjük, már csak $\displaystyle psi$ időbeli változási ütemét, $\displaystyle omega$_{$\displaystyle psi$}-t kell meghatároznunk, és segítségével a keresett szögsebesség:

$\displaystyle \omega_\gamma=\omega_\varphi+\omega_\psi=\left(1+{\omega_\psi\over\omega_\varphi}\right)\sqrt{{2g\over l}\sin\varphi}.$

Az $\displaystyle omega$_{$\displaystyle psi$}/$\displaystyle omega$_{$\displaystyle varphi$} arányt numerikusan (egymáshoz igen közeli szögek szögfüggvényeiből) akár egy zsebszámológép segítségével meghatározhatjuk, vagy differenciálszámítás felhasználásával zárt alakban is megadhatjuk:

$\displaystyle {\omega_\psi\over\omega_\varphi}=2{1+\tg^2\varphi\over1+4\tg^2\varphi}.$

- Az indítás pillanatában $\displaystyle omega$_{$\displaystyle varphi$}=$\displaystyle omega$_{$\displaystyle psi$}=0, így $\displaystyle omega$_{$\displaystyle gamma$} is nulla.

- A gyorsulásvektor vízszintes helyzeténél (azaz $\displaystyle varphi$=35,3^o-nál) $\displaystyle omega$_{$\displaystyle varphi$}=$\displaystyle omega$_{$\displaystyle psi$}$\displaystyle approx$3,36 s^-1, tehát $\displaystyle omega$_{$\displaystyle gamma$}$\displaystyle approx$6,72 s^-1. (Be lehet látni, hogy a gyorsulásvektor ebben a helyzetben változtatja leggyorsabban az irányát, $\displaystyle omega$_{$\displaystyle gamma$} itt a legnagyobb.)

- A pálya legmélyebb pontján $\displaystyle omega$_{$\displaystyle varphi$}$\displaystyle approx$4,23 s^-1, illetve $\displaystyle omega$_{$\displaystyle psi$}=$\displaystyle omega$_{$\displaystyle varphi$}/2, ahonnan $\displaystyle omega$_{$\displaystyle gamma$}$\displaystyle approx$6,64 s^-1.