Fizikából kitűzött gyakorlatok és feladatok
2002. január

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 230. Vegyünk egy végig egyforma szemekből álló láncot! (Lehet olyan is, amivel nemrég a karácsonyfát díszítettük.) Határozzuk meg a lánc és egy asztal felülete között a) a tapadási, b) a csúszási súrlódási együttható értékét! (6 pont)

Közli: Radnai Gyula, Budapest

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3488. Adott \(\displaystyle alpha\) hajlásszögű lejtőn alapjára állított, tömör, egyenes henger csúszik le. A súrlódási együttható . A henger alaplapján melyik pont tekinthető a lejtő által kifejtett nyomóerő támadáspontjának? (4 pont)

Közli: Rácz György, Mezőkövesd

P. 3489. Egy 150 g tömegű hógolyó 20 m/s sebességgel az ablaküveghez csapódik, és 0,01 s alatt megáll. Betörik-e az ablaküveg, ha az üveg a találat helyén legfeljebb 300 N nyomóerőt bír ki? (4 pont)

Közli: Szegedi Ervin, Debrecen

P. 3490. Hogyan lehet az, hogy egyes helikopterekre kell, másokra nem kell faroklégcsavar? (3 pont)

Lánczos Kornél verseny, Székesfehérvár

P. 3491. Egy villanymotor vonóereje 57,6 km/h sebesség esetén 310 kN. A tápfeszültség 3,6 kV, a nyolc villanymotor tekercseiben 230 A erősségű áram folyik. Határozzuk meg a motor hatásfokát! (3 pont)

,,Keresd a megoldást!'' verseny, Szeged

P. 3492. Mekkora annak a mosószeres oldatból formálódott buboréknak a sugara, amelyben a levegő sűrűsége egy ezrelékkel nagyobb, mint a környező levegőé? (\(\displaystyle alpha\)=0,033 N/m, p₀=10⁵ Pa.) (4 pont)

Közli: Varga István, Békéscsaba

P. 3493. Hidrogéngázzal az ábrán látható ABCA körfolyamatot végeztetjük. (p₁=2^.10⁵ Pa, V₁=2 m³, T_A=300 K.)

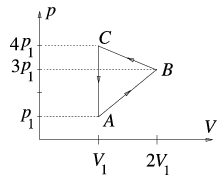
a) Mennyi hőt közlünk a gázzal az egyes részfolyamatokban?

b) Mennyi a gázon végzett összes munka? (4 pont)

Tornyai Sándor verseny, Hódmezővásárhely

P. 3494. A 20 cm sugarú, 8^.10^-7 C töltésű fémgömb körül mekkora annak a képzeletbeli koncentrikus gömbnek a sugara, amely a fémgömb elektrosztatikus terét két egyenlő energiájú tartományra osztja? Mekkora a fémgömb terének összenergiája? (5 pont)

Közli: Holics László, Budapest

P. 3495. Félgömb alakú üveglencse (n=1,5; R=4,8 cm) sík határfelülete matt. A félgömb szimmetriatengelyén pontszerű fényforrás található. A lencsén belépő fénysugarak egy fényes foltot hoznak létre a matt felületen. Hol van a fényforrás, amikor legkisebb a fényfolt? Mennyi ekkor a fényfolt átmérője? (5 pont)

Schwartz emlékverseny, Nagyvárad

P. 3496. Jelölje \(\displaystyle \lambda_{\min}\) a hidrogénatom által kibocsátott fény legrövidebb hullámhosszát! Kibocsáthat-e ez az atom \(\displaystyle 2\lambda_{\min}\) hullámhosszúságú fotont? (4 pont)

Nagy László verseny, Kazincbarcika

P. 3497. Egy 1 méter hosszú fonálingát a vízszintesig kitérítünk, majd elengedünk. Mekkora a fonál végén levő test gyorsulásvektorának szögsebessége, amikor a gyorsulásvektor a) függőleges, b) vízszintes helyzetű? (6 pont)

Közli: Sári Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. február 11.

Olimpiai levelezés A feladat vázlatos megoldása vagy végeredménye 1 hónapon belül elektronikus (esetleg hagyományos) levélben küldhető be a gnadig@komal.elte.hu címre (illetve a Szerkesztőségbe). Minden levélíró néhány napon belül névre szóló választ kap, melyből megtudhatja, hogy jó-e a megoldása, vagy ha nem, hol hibázott és hogyan léphetne tovább.

OLI. 5. Egy négyzet alakú vékony kereten szupravezető (elhanyagolhatóan kicsi elektromos ellenállású) vezetékből készült, rövidrezárt tekercs található. A tekercs önindukciós együtthatója L, tömege (a kerettel együtt) m, a négyzet oldala pedig \(\displaystyle ell\) hosszúságú.

A keret az egyik oldaléle körül súrlódásmentesen elfordulhat. A tekercs függőleges irányú, B₀ nagyságú homogén mágneses mezőben helyezkedik el. Kezdetben a keret síkja függőleges, és a tekercsben nem folyik áram.

a) A keretet lassan elfordítva vízszintes helyzetbe hozzuk. Mekkora M forgatónyomatékot kell kifejtenünk a keretre akkor, amikor a síkja \(\displaystyle alpha\) szöget zár be a függőlegessel. Adjuk meg M()-t a többi paraméter segítségével!

b) Mekkora W munkavégzés árán lehet a keretet vízszintes helyzetbe hozni? Fejezzük ki W-t a többi paraméter segítségével!

c) A keretet tovább forgatva azt tapasztaljuk, hogy az eredeti (függőleges) helyzetéhez képest 120^o-os helyzetben labilis, 180^o-nál pedig ismét stabil egyensúlyba kerül. Határozzuk meg, mekkora a két stabil egyensúlyi helyzet körüli kis lengések periódusidejének T_fent/T_lent aránya!