Matematikából kitűzött gyakorlatok és feladatok
2002. január

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok

Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 655. Barabás nagymamája egy ideje minden lottósorsoláskor félretesz perselyébe némi aprópénzt unokájának. A nagyi rendkívül precíz hölgy, és az alábbi szabályokat mindig betartja:

1) Csak fémpénzt tesz félre.

2) Egy szám kisorsolásakor a számnak megfelelő összeget teszi a perselybe, ügyelve arra, hogy a legkevesebb számú érmét használja fel.

3) A sorsolás végeztével mindig felírja, hogy melyik érméből mennyit dobott a perselybe.

Az egyik sorsolás után, ahol 7 számot sorsoltak az első 35 pozitív egész közül, nagyi azt jegyezte fel, hogy 3 db 20, 6 db 10, 5 db 5, 9 db 2 és 3 db 1 forintos érmét dobott a perselybe. Mik voltak a kisorsolt számok?

C. 656. Egy 21 250 Ft-os kabát árát leszállították egy engedményes vásár alkalmából. Majd a karácsonyi vásárban akciós áron még olcsóbb, 19 176 Ft lett. Hány százalékosak az engedmények, ha tudjuk, hogy mindkettő egyjegyű szám?

C. 657. Egy kúp és egy henger magassága is és térfogata is egyenlő. Mekkora a kúp nyílásszöge, ha a két test palástjának felszíne is megegyezik?

C.658. Oldjuk meg az

$\displaystyle {1\over x}+{1\over y}={1\over z}$

$\displaystyle {1\over x+y}+{1\over y-6}={1\over z}$

$\displaystyle {1\over x+24}+{1\over y-15}={1\over z}$

egyenletrendszert.

C. 659. A 0$\displaystyle le$t$\displaystyle le$ $pi$ valós paraméter mely értékei esetén nincs megoldása a sin (x+t)=1-sinx egyenletnek?

A B pontversenyben kitűzött feladatok

A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3512. Keressük meg a 81-nek azt a legkisebb többszörösét,

a) amelyik csak az 1

b) amelyik csak az 1 és a 0 számjegyeket tartalmazza.

(4 pont)

B. 3513. Két körvonal nincs egy síkban, és pontosan két közös pontjuk van. Mutassuk meg, hogy van olyan gömbfelület, amelyre illeszkednek. (3 pont)

B. 3514. Az ABC háromszög magasságai AA₁, BB₁ és CC₁, területe t. Bizonyítsuk be, hogy az ABC háromszög pontosan akkor szabályos, ha

AA₁^.AB+BB₁^.BC+CC₁^.CA=6t.

(3 pont)

B. 3515. Bizonyítsuk be, hogy a $\big[\sqrt2\cdot n\big]$ alakú számok között végtelen sok 2-hatvány van. (4 pont)

B. 3516. A füzetlapra rajzoltunk egy 5 cm-es zárt töröttvonalat. Mutassuk meg, hogy le tudjuk takarni egy 20 Ft-os érmével (az érme átmérője nagyobb, mint 2,5 cm). (3 pont)

B. 3517. Bizonyítsuk be, hogy 71|61!+1. (4 pont)

Javasolta: Róka Sándor, Nyíregyháza

B. 3518. Igaz-e, hogy ha két tetraéder lapjai megfeleltethetők úgy, hogy az egymásnak megfeleltetett lapok egyenlő területűek, akkor a két tetraéder térfogata is egyenlő? (4 pont)

B. 3519. Az OA₁A₂A₃ tetraéder OA_i élén lévő, O-tól és A_i-től különböző B_i és C_i pontokra (i=1,2,3) teljesül, hogy az A₁A₂, B₁B₂ és C₁C₂ egyenesek is, és az A₁A₃, B₁B₃ és C₁C₃ egyenesek is egy ponton mennek át. Mutassuk meg, hogy ekkor az A₂A₃, B₂B₃ és C₂C₃ egyenesek egy ponton mennek át vagy párhuzamosak. (4 pont)

B. 3520. A valós számok közül bizonyosakat pirosra festünk, mégpedig úgy, hogy ha az x szám piros, akkor az x+1 és 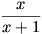${x\over x+1}$ számokat is pirosra festjük. Mely számok lesznek pirosak, ha kezdetben csak az 1 piros? (5 pont)

B. 3521. Egy baktériumtörzs minden tagja egy óra leteltével vagy elpusztul vagy pedig kettéosztódik. Ha az osztódás valószínűsége p, akkor mennyi a valószinűsége annak, hogy egy kiszemelt baktérium leszármazottai sosem halnak ki? (5 pont)

Az A pontversenyben kitűzött nehezebb feladatok

Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 281. Adott a síkon véges sok pont úgy, hogy semelyik három nem esik egy egyenesre. Bizonyítsuk be, hogy a pontokat ki lehet színezni két színnel -- pirossal és kékkel -- úgy, hogy minden félsík, amelyik legalább három pontot tartalmaz, tartalmazzon piros és kék színű pontot is.

Soukup Lajos, Budapest

A. 282. Léteznek-e olyan f, g és h racionális törtfüggvények, amelyek minden együtthatója racionális szám, és amelyekre

(f(x))³+(g(x))³+(h(x))³=x?

A. 283. Legyen n egész szám. Bizonyítsuk be, hogy ha az x²+xy+y²=n egyenletnek létezik racionális számokból álló megoldása, akkor létezik egész számokból álló megoldása is.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség

Budapest 112, Pf. 32. 1518

illetve

megoldas@komal.elte.hu

tájékoztatónkat

Már regisztráltál?
Új vendég vagy?