A 2002 februári A-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A. 284. Legyen f a véges S halmaz részhalmazain értelmezett függvény. Igazoljuk, hogy ha S tetszőleges A, B részhalmazaira

f(S\A)=f(A) és max(f(A),f(B)) $\displaystyle ge$ f(A $\displaystyle cup$ B),

akkor f legfeljebb |S| különböző értéket vesz fel.

Schweitzer Miklós Emlékverseny, 2001

1. megoldás. Az S= $\displaystyle emptyset$ esetben az állítás nem igaz; a továbbiakban feltételezzük, hogy S nem üres.

Teljes indukciót alkalmazunk; |S|=1 és |S|=2 esetén éppen 1, illetve 2 komplementer részhalmaz pár van, ezért nem is lehet több függvényérték. Legyen tehát |S|>2, és tegyük fel, hogy kisebb elemszám esetén az állítás igaz.

Legyen f legnagyobb értéke m. Először megmutatjuk, hogy van olyan X={x} egyelemű részhalmaza S-nek, amelyre f(X)=m. Tekintsük azokat a részhalmazokat, amelyekhez f az m számot rendeli. Ezek között a komplementer tulajdonság miatt van nem üres is. Vegyük tehát a legkisebb olyan nemüres X részhalmazt, amire f(X)=m. Ha X legalább kételemű lenne, akkor felbomlana két kisebb nem üres halmaz uniójára: X=X₁ $\displaystyle cup$ X₂, de ekkor max(f(X₁),f(X₂)) $ge$ f(X₁ $\displaystyle cup$ X₂)=f(X)=m miatt f(X₁) és f(X₂) valamelyike is m. Az X halmaz tehát egyelemű.

Legyen R=S\X, és definiáljuk a g:P(R) $\displaystyle to$ R függvényt a következőképpen: tetszőleges A $\displaystyle subset$ R esetén legyen

g(A)=min(f(A),f(A $cup$ X))=min(f(A),f(R\A)).

Megjegyezzük, hogy tetszőleges A $\displaystyle subset$ R esetén max(f(A),f(A $\displaystyle cup$ X))=m. Ugyanis

m=f(X)=f(S\X)=f(A $cup$ (R\A)) $\displaystyle le$ max(f(A),f(R\A))=

=max(f(A),f(S\(R\A)))=max(f(A),f(A $cup$ X)).

A továbbiakban megmutatjuk, hogy a g függvényre teljesül az indukciós feltétel, azaz tetszőleges A,B $subset$ R esetén g(R\A)=g(A) és g(A $cup$ B) $le$ max(g(A),g(B)). Az indukciós feltevés szerint tehát g-nek legfeljebb (|S|-1)-féle értéke lehet. Mivel tetszőleges A $\displaystyle subset$ T halmazra f(A) és f(A+X) egyike m, másika g(A), ebből következik, hogy f értékkészlete legfeljebb csak az m számmal lehet bővebb g értékkészleténél.

A g(R\A)=g(A) tulajdonság g definíciójából leolvasható.

Ha g(A) és g(B) valamelyike m, akkor a g(A $\displaystyle cup$ B) $\displaystyle le$ max(g(A),g(B)) triviálisan teljesül. Tegyük tehát fel, hogy g(A) és g(B) kisebb, mint m, azaz f(A) és f(A $\displaystyle cup$ X), illetve f(B) és f(B $cup$ X) valamelyike kisebb m-nél. Ha f(A)<m, akkor legyen C=A, ellenkező esetben legyen C=A $cup$ X. Hasonlóképpen legyen f(B)<m esetén D=B, egyébként D=B $\displaystyle cup$ X. Ekkor f(C)=g(A) és f(D)=g(B), a C $cup$ D halmaz pedig vagy A $\displaystyle cup$ B, vagy pedig A $\displaystyle cup$ B $\displaystyle cup$ X. Ezért

max(g(A),g(B))=max(f(C),f(D)) $ge$ f(C $cup$ D) $ge$

$\displaystyle ge$ min(f(A $\displaystyle cup$ B),f(A $cup$ B $cup$ X))=g(A $\displaystyle cup$ B).

A g függvényre tehát teljesülnek a feltételek.

2. megoldás (Csóka Endre megoldása). A megoldás alapja a következő lemma:

Lemma. Legyen v tetszőleges valós szám, és legyen S_v az S azon részhalmazainak a halmaza, amelyekhez az f függvény v-nél nem nagyobb értéket rendel:

S_v={X $subset$ S: f(X) $\displaystyle le$ v}.

Ekkor |S_v| vagy 0, vagy pedig egy 1-től különböző kettőhatvány.

A lemma bizonyítása. Először megállapítjuk, hogy S_v zárt a komplementer-, unió-, metszet- és különbségképzére, azaz tetszőleges S_v-beli X,Y halmazok esetén S\X, X $cap$ Y, X $cup$ Y és X\Y is S_v-beli. Az első kettő azért igaz, mert f(S\X)=f(X) $le$ v, illetve f(X $\displaystyle cup$ Y) $\displaystyle le$ max(f(X),f(Y)) $le$ max(v,v)=v; a metszet és a különbség pedig kifejezhető a komplementer és unió műveletekkel.

Az unióra és komplementerképzésre zártság egyik következménye, hogy ha S_v nem üres, akkor S $in$ S_v.

A komplementerképzésre zártságból következik, hogy ha S_v-nek van legalább egy eleme, akkor az elem komplementere is elem, ezért S_v elemei párokba állíthatók; S_v tehát nem lehet egyelemű.

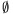Nevezzük S_v atomjainak a nem üres elemei közül a minimálisakat. Egy nem üres A $in$ S_v halmaz tehát akkor atom, ha X $subset$ A, X $\displaystyle in$ S_v esetén X= $emptyset$ vagy X=A.

Az atomok definíciójából két nagyon fontos dolog következik. Az első, hogy ha A $\displaystyle in$ S_v egy atom és X $in$ S_v tetszőleges halmaz, akkor A vagy X-nek, vagy (S\X)-nek részhalmaza. Ellenkező esetben ugyanis A\X egy nem üres, valódi részhalmaza lenne A-nak, ami ellentmond annak, hogy A atom. A másik fontos következmény, hogy az atomok páronként diszjunktak. Ha ugyanis valamelyik két atom nem diszjunkt, akkor az előbbiek szerint tartalmazzák egymást, vagyis a két atom ugyanaz.

Megmutatjuk, hogy az S halmaz minden elemét S_v-nek pontosan egy atomja tartalmazza. Mivel az atomok páronként diszjunktak, x legfeljebb egy atomnak lehet eleme; csak azt kell tehát igazolnunk, hogy létezik ilyen atom. Legyen x $\displaystyle in$ S egy tetszőleges elem. Tekintsünk az x-et tartalmazó S_v-beli halmazok közül egy minimálisat; legyen ez A. Ha A nem atom, akkor nem minimális, tehát van egy X $\displaystyle subset$ A részhalmaza, ami nem üres, de nem is egyenlő A-val. Ekkor X és A\X is S_v-beli, valódi részhalmaza A-nak, és egyikük tartalmazza x-et. Ez pedig ellentmond annak, hogy A minimális az x-et tartalazó S_v-beli halmazok közül. A tehát atom.

Az eddigiekből következik, hogy tetszőleges X $in$ S_v halmaz egyértelműen írható fel S_v-beli atomok uniójaként. Tetszőleges x $\displaystyle in$ S elemhez legyen A_x az az atom, amelyre x $\displaystyle in$ A_x. Az X halmaz egyértelmű felírása a következő:

$\displaystyle X=\bigcup_{x\in X}A_x.$

A jobboldalon ugyanis minden atom részhalmaza X-nek, tehát a jobboldal részhalmaza X-nek; másrészt a jobboldal az X-nek minden elemét tartalmazza, mert tetszőleges x $in$ X esetén az x-et tartalmazó A_x szerepel a tagok között. Már csak azt kell igazolnunk, hogy ez az egyetlen felírás. Ha x $\displaystyle in$ X, akkor X egy tetszőleges felírásban mindenképpen szerepelnie kell az A_x atomnak, mert csak ez az atom tartalmazza x-et. Az X-szel diszjunkt atomok pedig nem szerepelhetnek X felírásában.

Legyenek S_v atomjai A¹,...,A^k. Az előbbiek szerint minden S_v-beli X halmazhoz egyértelműen létezik egy olyan I $\displaystyle subset$ {1,2,...,k} indexhalmaz, amelyre X= $\displaystyle cup$ _{i $\displaystyle in$ I}Aⁱ. Megfordítva, tetszőleges I indexhalmaz esetén $\displaystyle cup$ _{i $\displaystyle in$ I}Aⁱ egy S_v-beli halmaz. Az S_v-beli halmazok tehát kölcsönösen egyértelműen megfeleltethetők az {1,2,...,k} halmaz részhalmazainak. Az ilyen részhalmazok száma 2^k, tehát |S_v|=2^k. Ezzel a lemmát igazoltuk.

Már csak a feladat állításának igazolása van hátra. Legyenek az f függvény értékei v₁<v₂<...<v_n. Tekintsük az S_v₁,S_v₂,...,S_{v_n} halmazokat. Ezek egy bővülő láncot alkotnak:

S_v₁ $subset$ S_v₂ $subset$ ... $subset$ S_{v_n}.

A halmazok nem üresek, és semelyik kettő nem egyezhet meg. Ezért a lemma alapján |S_v₁|<|S_v₂|<...<|S_{v_n}| különböző, 1-nél nagyobb 2-haványok, és így |S_{v_n}| $ge$ 2ⁿ. Másrészt S_{v_n} az S halmaz összes részhalmazából áll, tehát |S_{v_n}|=2^|S|. Ezzel azt kaptuk, hogy n $\displaystyle le$ |S|.

Megjegyzés. Olyan példát nem nehéz konstruálni, amikor f értékkészlete éppen |S| elemű. Legyen S={1,2,...,n}, f(S)=f(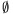 $emptyset$ )=0, továbbá tetszőleges S-től és az üres halmaztól különböző X részhalmaz esetén legyen f(X) a legnagyobb olyan S-beli szám, amelyre f(X) és f(X)-1 közül pontosan az egyik eleme X-nek. Például n=6 esetén f({1,2,5})=5.

A. 285. Bizonyítsuk be, hogy ha az a>b>c>d>0 egész számokra

a²+ac-c²=b²+bd-d²,

akkor ab+cd összetett.

Megoldás. Tegyük fel, hogy p=ab+cd prím. Ekkor ab $equiv$ -cd (mod p), és

0=b²(b²+bd-d²)-b²(a²+ac-c²)=b²(b²+bd-d²)-a²b²-ab²c+b²c² $equiv$

$\displaystyle equiv$ b²(b²+bd-d²)-c²d²+bc²d+b²c²=(b²+c²)(b²+bd-d²) (mod p).

A b²+c² és b²+bd-d² számok közül tehát valamelyik osztható p-vel.

Ha b²+c² osztható p-vel, akkor 0<b²+c²<2(ab+cd)=2p miatt b²+c²=p. Ebben az esetben ab+cd=b²+c². Ezt modulo b vizsgálva látjuk, hogy c(c-d) oszható b-vel. A b és a c relatív prímek (különben ab+cd nem lehetne prímszám), tehát c-d osztható b-vel. Ez viszont ellentmondás, mert 0<c-d<b.

Ha b²+bd-d² osztható p-vel, akkor 0<b²+bd-d²<2(ab+cd)=p miatt b²+bd-d²=p. Ekkor ab+cd=b²+bd-d²=a²+ac-c². Ezt modulo a és modulo b vizsgálva láthatjuk, hogy (c+d)c osztható a-val, illetve (c+d)d osztható b-vel. Mivel ab relatív prím cd-hez, ebből az következik, hogy c+d osztható a-val és b-vel is. Mivel azonban 0<c+d<2a és 0<c+d<2b, ez egyszerre nem lehetséges.

A. 286. Határozzuk meg mindazokat az f:R $to$ R folytonos függvényeket, amelyekre 1+xy $\displaystyle ne$ 0 esetén

$\displaystyle f\left({x+y\over1+xy}\right)={f(x)f(y)\over|1+xy|}.$

Győrfi Zoltán és Ligeti Gábor ötletéből

Megoldás. Legyen

$\displaystyle g(u)=\left|{1+u\over2}\right|\cdot f\left({u-1\over u+1}\right),$

vagy másképpen

$\displaystyle f(x)=|1-x|\cdot g\left({1+x\over1-x}\right).$

Egy kis számolással ellenőrizhető, hogy ezzel a helyettesítéssel g(uv)=g(u)^.g(v). Ez háromféleképpen lehetséges:

a) g(u) $\displaystyle equiv$ 0; ekkor f(x) $equiv$ 0.

b) g(u)=|u|^{$\displaystyle alpha$}, ahol $alpha$ valós szám. Ekkor f(x)=|1+x|^.|1-x|^1-. A folytonosság miatt 0 $\displaystyle le$ $alpha$ $le$ 1.

c) g(u)=sgnu^.|u|. Ekkor f(x)=sgn(1-|x|)^.|1+x|^.|1-x|^1-. Ezúttal 0< $alpha$ <1.

Megjegyzés. Az 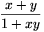${x+y\over1+xy}$ tört a hiperbolikus tangens addíciós képletére hasonlít:

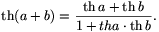
$\th(a+b)={\th a+\th b\over1+tha\cdot\th b}.$

A megoldásban látott helyettestés során a 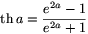$\th a={e^{2a}-1\over e^{2a}+1}$ törtben e^2a helyére írtunk u-t.

Már regisztráltál?
Új vendég vagy?