A 2002. februári C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 660.  Hányféleképpen lehet a 8x8-as sakktábla mezői közül két különbözőt kiválasztani úgy, hogy a középpontjukat összekötő szakasz felezőpontja is egy mező középpontjába essen?

Megoldás. A sakktábla mezőit (ill. azok középpontjait) a szokásos módon ,,koordinátázhatjuk'' úgy, hogy koordinátatengelyeknek a tábla két, egymásra merőleges szélső sorában a középpontok alkotta egyenest választjuk. Így minden mező koordinátái 0-tól 7-ig terjedő egész számok. Az (a,b) és a (c,d) koordinátájú középpontokat összekötő szakasz felezőpontjának koordinátái \(\displaystyle (\frac{a+c}{2},\frac{b+d}{2})\); ez éppen akkor esik egy mező középpontjába, ha a+c és b+d páros, azaz ha a és c azonos paritású, akárcsak b és d.

Az (a,b) pont a tábla 64 mezője közül bármelyik középpontja lehet, ennek kiválasztása után c értékét az a paritásával megegyező 4 szám bármelyikének választhatjuk, ugyanígy és tőle függetlenül d is 4-féle lehet. Azért, hogy a két kiválasztott pont különböző legyen, a 4^.4=16-nál 1-gyel kevesebb a megfelelő (c,d) párok száma. Mivel így a két kiválasztott pont sorrendjére is tekintettel voltunk, a megfelelő pontpárok száma \(\displaystyle \frac{1}{2}\cdot64\cdot15=480\).

C. 661.  Mi a feltétele annak, hogy egy 9-re és egy 7-re végződő egész szám szorzata 63-ra végződjön?

Megoldás. Legyenek a keresett számok A=100x+10a+9, B=100y+10b+7 (a és b az utolsó előtti számjegyek, x és y egész). Ekkor AB=100v+10(7a+9b)+63 pontosan akkor végződik 63-ra, ha 7a+9b=10b+(7a-b) osztható 10-zel, azaz ha b megegyezik 7a utolsó számjegyével. Az A és B két utolsó jegye tehát a következők valamelyike: (09;07), (19;77), (29;47), (39;17), (49;87), (59;57), (69;27), (79;97), (89;67), (99;37).

C. 662.  Egy téglatest térfogata 8 cm³. Ha a téglatest minden élét 1 centiméterrel megnöveljük, akkor egy 27 cm³ térfogatú téglatestet kapunk. Mekkora térfogatú téglatestet kapunk, ha ismét megnöveljük az éleket 1-1 centiméterrel?

Megoldás. A téglatest éleit a,b,c-vel jelölve abc=8 és (a+1)(b+1)(c+1)=27. A második egyenletben a beszorzásokat elvégezve: abc+(ab+ac+bc)+(a+b+c)+1=27, azaz (ab+ac+bc)+(a+b+c)=18. A számtani és a mértani középre vonatozó egyenlőtlenség szerint \(\displaystyle ab+ac+bc\geq3\cdot\root3\of{ab\cdot ac\cdot bc}=3\cdot\root3\of{(abc)^2}=3\cdot\root3\of{64}=12\) és \(\displaystyle a+b+c\geq3\cdot\root3\of{abc}=6\), így 18=(ab+ac+bc)+(a+b+c)\(\displaystyle ge\)12+6=18. Tehát mindkét egyenlőtlenségben egyenlőség áll, ezért a=b=c (és ab=ac=bc), azaz a=b=c=2. A téglatest éleit további 1 - 1 centiméterrel megnövelve 4³=64 térfogatú téglatestet kapunk.

C. 663.  Egy hegyesszögű háromszög alakú papírlapnak leszakadt a legnagyobb szöget tartalmazó csúcsa. A papír megmaradt részén szerkeszük meg a háromszög köré írható kör sugarát.

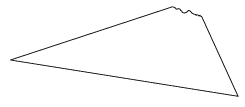
Róka Sándor (Nyíregyháza) javaslata nyomán

Megoldás. Szerkesszük meg az épen maradt AB oldal F felezőpontját. Vegyük fel az AF szakaszon az A' pontot olyan közel az F-hez, hogy az FB szakaszon F-től FA' távolságra levő B' ponton át a csonka a oldallal húzott párhuzamos a papírlapon messe az A' ponton át a b oldallal megszerkesztett párhuzamost. Így A' és B' egy, az eredeti háromszöghöz hasonló háromszögnek a csúcsai.

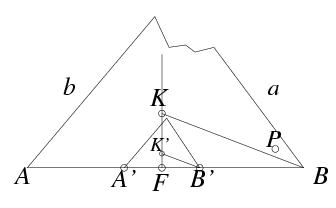
E kis háromszög köré írható kör K' középpontját meg tudjuk szerkeszteni. A B ponton keresztül B'K'-vel húzott párhuzamos az FK' félegyenesből kimetszi az eredeti háromszög köré írható kör K középpontját, ha az egyáltalán a papírlapon van. Mivel azonban nem szükségszerűen van ott, egy kerülő megoldást alkalmazunk, ami ugyancsak a szelőtétel segítségével adja meg a BK szakasz hosszát. Vegyünk fel a papírlapon B-hez ,,egészen közel'' egy P pontot úgy, hogy a PAB háromszög teljes egészében a papírlapon legyen, és PA hossza nagyobb legyen FB-nél (az AB oldal felénél). Mérjük fel az AP félegyenesre A-ból kiindulva az FB' és az FB távolságokat, az AB félegyenesre pedig ugyancsak A-ból a K'B' távolságot. Az FB' és K'B' hosszúságú szakaszok végpontját összekötő szelővel az FB hosszúságú szakasz végpontján át húzott párhuzamos az AB-ből éppen egy KB hosszúságú szakaszt metsz ki a párhuzamos szelők tétele miatt. Ez a szakasz valőban elfér az AB-n, mivel egy r sugarú körbe írt háromszög legnagyobb oldalának a hossza legalább \(\displaystyle \sqrt{3}\)r">.

C. 664.  Határozzuk meg az y=x²+1 és az x=y²+1 egyenletű parabolák az y=x egyenletű egyenessel párhuzamos érintőinek távolságát.

Megoldás. Az x=y²+1 egyenletű parabola éppen az y=x²+1 egyenletű parabola tükörképe az y=x egyenletű egyenesre. Ezért a két érintő távolsága a második parabola érintési pontjának az y=x egyenletű egyenestől mért távolságának a kétszerese.

Az y=x²+1 egyenletű parabola a abszcisszájú pontjában húzott érintőjének a meredeksége 2a, ezért 2a=1 szerint az érintési pont koordinátái: \(\displaystyle ({{1}\over{2}};{{1}\over{4}}+1={{5}\over{4}})\). Ennek a pontnak a \(\displaystyle -{{x}\over{\sqrt{2}}}+{{y}\over{\sqrt{2}}}=0\) egyenletű egyenestől való távolsága \(\displaystyle -{{1/2}\over{\sqrt{2}}}+{{5/4}\over{\sqrt{2}}}={{3\sqrt{2}}\over{8}}\), tehát a két érintő távolsága \(\displaystyle 2\cdot{{3\sqrt{2}}\over{8}}={{3\sqrt{2}}\over{4}}\).