Matematikából kitűzött gyakorlatok és feladatok
2002. április
Kérjük, olvassa el a versenykiírást.
 |
A C pontversenyben kitűzött gyakorlatokMinden C-jelű feladat helyes megoldásáért 5 pont jár. |
C. 670. Egy 3x3-as táblázatba beírtuk az első kilenc pozitív egész számot, mindegyiket egyszer. Tegyük föl, hogy a három sorban balról jobbra, a három oszlopban fölülről lefelé, illetve a bal fölső csúcsból kiinduló átlón kiolvasható háromjegyű számok mindegyike osztható 11-gyel. Mekkora lehet a jobb fölső sarokból kiinduló átlón kiolvasható háromjegyű szám értéke?
Javasolta: Kiss Sándor, Nyíregyháza
C. 671. Egy 36 cm átmérőjű lábosba beleállítottunk egy 6 cm és egy 12 cm sugarú befőttesüveget. Legfeljebb mekkora sugarú befőttesüveg állítható be a többi mellé a lábosba?
C. 672. Egy téglatest A csúcsából kiinduló éleinek hossza 1, 2, 3 egység. Ezen élek A-tól különböző végpontjai egy háromszöget határoznak meg. Milyen messze van az A pont a háromszög síkjától?
C. 673. A 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 számok közül kétszer választunk véletlenszerűen. (Ugyanazt a számot kétszer is kiválaszthatjuk.) Minek nagyobb a valószínűsége: annak, hogy a két szám összege, vagy annak, hogy a különbségük osztható 3-mal?
C. 674. Oldjuk meg az alábbi egyenletet:
\(\displaystyle {x\over20}=\left({5\over2}\right)^{\log_x50}.\)
 |
A B pontversenyben kitűzött feladatokA B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe. |
B. 3542. Bizonyítsuk be, hogy ha egy 111...1 alakú szám
osztható 7-tel, akkor osztható 37-tel is. (3 pont)
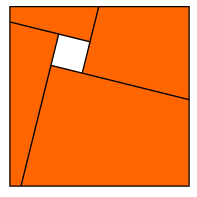
B. 3543. Egy négyzet alakú papírlapon egy négyzet alakú
lyuk van. A lyuk mindegyik oldalát meghosszabbítottuk pozitív
körüljárás szerinti irányban. Tegyük fel, hogy az így kapott
félegyenesek a papírt négy négyszögre bontják az ábra
szerint. Igazoljuk, hogy ebből a négy négyszögből másképpen is
összeállítható egy négyzet, amelyben van egy négyzet alakú lyuk.
(4 pont)
Gál Péter ötletéből
B. 3544. Mutassuk meg, hogy a háromszög hozzáírt körei közt
van olyan, amelynek a sugara legalább háromszorosa a beírt kör
sugarának. (3 pont)
B. 3545. Bizonyítsuk be, hogy
\(\displaystyle {n^2-n\over2}\leq\big\{\sqrt1\big\}+\big\{\sqrt2\big\}+\ldots+\big\{\sqrt{n^2}\big\}\leq{n^2-1\over2},\)
ahol {x} az x törtrészét jelöli. (4 pont)
B. 3546. Egy kockát egy síkkal metszve olyan ABCDEF
hatszöget kapunk, amelynek AD, BE, CF átlói egy
ponton haladnak át. Bizonyítsuk be, hogy a metsző sík áthalad a kocka
középpontján. (5 pont)
B. 3547. Bizonyítsuk be, hogy ha az f függvényre
\(\displaystyle f(x+1)+f(x-1)=\sqrt2f(x)\)
minden valós x-re teljesül, akkor a függvény
periodikus. (4 pont)
B. 3548. Egy különböző pozitív egészekből álló végtelen
számtani sorozat minden elemét elosztjuk a legnagyobb
prímosztójával. Lehet-e az így kapott sorozat korlátos? (4
pont)
B. 3549. Bizonyítsuk be, hogy tetszőleges x valós
szám esetén
cos cos x\(\displaystyle ge\)|sin x|.
(4 pont)
Javasolta: Szobonya László, Budapest
B. 3550. Az ABC háromszög A-ból és
B-ből induló magasságvonalai az M pontban metszik
egymást, a szemközti oldalakat pedig az A1 és a
B1 pontokban. Tegyük fel, hogy az
A1B1 egyenes az AB oldalt
D-ben metszi. Bizonyítsuk be, hogy a DM egyenes
merőleges a C-ből induló súlyvonalra. (5 pont)
B. 3551. Legyenek az a, b, c, d
olyan pozitív egészek, melyekre
a2+b2+ab=c2+d2+cd.
Bizonyítsuk be, hogy a+b+c+d összetett
szám. (5 pont)
 |
Az A pontversenyben kitűzött nehezebb feladatokMinden A-jelű feladat helyes megoldásáért 5 pont jár. |
A. 290. Adott véges sok négyzet alakú papírlap, amelyek területének összege 4 egység. Bizonyítsuk be, hogy lefedhető velük egy egységnyi négyzet.
Allan Wilson, Anglia
A. 291. Oldjuk meg az
\(\displaystyle x=\sqrt{2+\sqrt{2-\sqrt{2+x}}}\)
egyenletet.
A. 292. Egy világvárosban n metróvonal van (n>4). Egy állomáson legfeljebb három metróvonal találkozik, és bármelyik két különböző metróvonalhoz létezik egy harmadik, amelyikre mindkettőről át lehet szállni. Igazoljuk, hogy a városban legalább \(\displaystyle {5\over6}(n-5)\) metróállomás van.
A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:
- KöMaL Szerkesztőség
Budapest 112, Pf. 32. 1518
- megoldas@komal.elte.hu (Az interneten keresztül történő
beküldésről olvassa el tájékoztatónkat)

