Fizikából kitűzött gyakorlatok és feladatok
2002. szeptember

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 235. Határozzuk meg egy korong alakú mágnes körül több pontban az indukcióvektor irányát! Használjunk először vasreszeléket, majd iránytüt! (6 pont)

A Bay Zoltán verseny kísérleti feladata nyomán

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3541. Egy vízzel félig töltött edényben egy vékony falú, zárt üveggömb úszik. Az asztalon áll még két azonos méretü pohár is, teletöltve vízzel. Ha az egyik pohár tartalmát beleöntjük az edénybe, azt tapasztaljuk, hogy az üveggömb jobban bemerül, ha a másik pohár vizet öntjük az edénybe, az üveggömb kevésbé merül be a vízbe. Hogyan lehetséges ez? (3 pont)

Frank János verseny, Szeged

P. 3542. Az ábrán látható oldalcsöves edény, valamint víz és mérőhenger felhasználásával hogyan becsülhetjük meg egy adott kémcső tömegét?

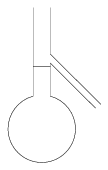
(3 pont)

Becslési verseny, Sárospatak

P. 3543. Éva, a 176 cm magas manöken a falra akasztott tükörben nézi magát. A tükör függőleges, magassága 75 cm. Éva egyenesen áll, és a szeme a talaj fölött 168 cm magasan van. Láthatja-e a saját szemét, ha még éppen látja a cipőjét? (3 pont)

Tarján Imre verseny, Szolnok

P. 3544. Az ábrán látható edényből kiszivattyúzták a levegőt. A felső gömbben víz van. Ha az alsó gömböt cseppfolyós nitrogénnel hütik, akkor a felső gömbben levő víz egy idő után megfagy. Mivel magyarázható a jelenség? Lehetséges-e, hogy a víz forrás közben fagy meg?

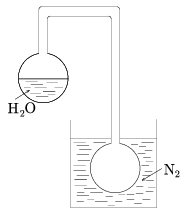
(4 pont)

Bródy Imre verseny, Ajka

P. 3545. Két egyforma nagy, gömb alakú, vízzel telt üveg akvárium áll szorosan egymás mellett az asztalon. Mindkét akvárium középpontjában egy-egy kis hal úszik. Mekkorának, és milyen távolságban látják egymást a halacskák? A víz törésmutatója 1,33. (5 pont)

Holló András verseny, Jászberény

P. 3546. Az ürben egymástól 20 m távolságra lebeg egy 1000 kg-os ürhajó, benne egy 100 kg-os asztronauta, és egy 100 kg-os mühold. Az ürhajóról az asztronauta úgy rugaszkodik el -- megigazítani egy antennaelemet a müholdon --, hogy a sebessége az ürhajóhoz képest 1,1 m/s. A munkát 130 másodperc alatt végzi el, utána 100 másodperc alatt szeretne visszatérni az ürhajóhoz. A müholdhoz képest mekkora sebességgel kell elrugaszkodnia, hogy terve sikerüljön? (4 pont)

Öveges József emlékverseny, Tata

P. 3547. A geostacionárius müholdakat a következő módon állítják pályára: a mühold először a Földhöz közeli parkolópályán mozog, majd a hajtómüveit rövid ideig bekapcsolva olyan ellipszispályára állítják, amelynek földközel-pontja a parkolópályán, földtávol-pontja pedig a geostacionárius pályán van. Ezt elérve, a hajtómüveket újra müködésbe hozva körpályára állítják a müholdat.

Tegyük fel, hogy a parkolópálya a Föld felszínétől 200 km-re levő körpálya. Mennyi idő alatt ér innen a mühold a geostacionárius pálya magasságába? (5 pont)

Zemplén Győző verseny, Nagykanizsa

P. 3548. Az ábrán látható elektromos hálózatban a fogyasztók ellenállása R₁=300 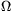, illetve R₂=700 \(\displaystyle Omega\). Az áramforrás elektromotoros ereje U₀=50 V, belső ellenállása elhanyagolható. A kondenzátor kapacitása C=50 F. A voltmérőt az A és B pontok közé kapcsolva azt tapasztaljuk, hogy U₁=14,5 V feszültséget mutat.

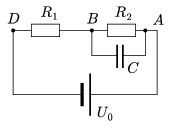
a) Mekkora a voltmérő ellenállása? Hány elektron távozik a kondenzátor negatív fegyverzetéről a feszültségmérés ideje alatt?

b) Mit mutat a voltmérő, ha a B és D pontok közé kapcsoljuk? Mekkora e mérés abszolút, illetve relatív hibája?

c) Legalább mekkora legyen egy voltmérő ellenállása, hogy a B és D pontok közé kapcsolva a mérés relatív hibája 1% legyen? (5 pont)

Vermes Miklós feladata nyomán

P. 3549. Egy optikai rácsot 589 nm hullámhosszúságú párhuzamos fénynyalábbal világítunk meg. A rácstól 3 méterre lévő ernyőn a nulladrendü és az elsőrendü elhajlási maximum egymástól 20 cm-re látható.

a) Centiméterenként hány karcolat van a rácson?

b) Milyen messze van a másodrendü elhajlási maximum az elsőrendütől? (4 pont)

Jedlik Ányos verseny, Győr

P. 3550. Egy, a Föld körül keringő ürhajóban egy 50 g tömegü, lebegő állapotban levő lézerceruza hirtelen bekapcsolódik, és egy órán keresztül 3 mW teljesítménnyel 500 nm hullámhosszúságú fényt sugároz.

a) Hány fotont sugároz ki a lézer ennyi idő alatt?

b) Becsüljük meg, hogy mekkora sebességre tesz szert és mekkora utat tesz meg az ürhajóban ennyi idő alatt a lézerceruza! (5 pont)

Wigner Jenő verseny, Békéscsaba

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.elte.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. október 11.