Matematikából kitűzött gyakorlatok és feladatok
2002. szeptember

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 680. Egy kilenctagú választó testület három jelölt közül választ. Mindegyikük rangsorolja őket, az elsőnek 3, a másodiknak 2, a harmadiknak pedig 1 pontot ad. Összesítve a jelöltek pontszámát kiderült, hogy a sorrend egyértelmü, hármuk pontszáma különböző. A testület egyik tagja észrevette, hogy ha a választást úgy bonyolították volna le, hogy mind a kilencen csak egy jelöltet választanak ki és annak adnak 1 pontot, akkor a jelöltek sorrendje megfordulna. Hány pontot kaptak eredetileg a jelöltek?

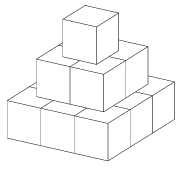
C. 681. Az ábrán látható három emeletes ,,piramist'' 1 cm³-es kockákból építettük, felszíne 42 cm². Ennek mintájára készítettünk egy nagyobb ,,piramist'' is, amelynek 2352 cm² a felszíne. Hány emeletes?

C. 682. A 2002-es adóbevallásnál azoknak, akiknek az éves bruttó jövedelme 1 050 000 forintnál több volt, a többlet 40%-án kívül 267 000 forintot kellett adóként befizetni. Mekkora havi bruttó jövedelem esetén lett a jövedelem 30%-a az adó?

Fried Ervin, Budapest

C. 683. Az ABC egyenlő szárú derékszögü háromszögben AC=BC. Az A csúcsból induló szögfelező a BC befogót a P pontban metszi. Igazoljuk, hogy a PB szakasz hossza egyenlő az ABC háromszög beírt körének átmérőjével.

C. 684. Oldjuk meg az

x-xy+y=1

x²+y²=17

egyenletrendszert.

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3562. Egy nyolcéves kislány konvex hétszög alapú tortát kapott a születésnapjára. A tortát a hétszög átlói mentén függőleges vágásokkal szeletelték föl. Az ünnepelt nyolcszög alapú szeletet szeretne kapni. Teljesülhet-e a kívánsága? (3 pont)

B. 3563. Legalább mekkora t érték esetén teljesül minden nemnegatív x, y valós számra a \(\displaystyle \sqrt{xy}\leq t(2x+3y)\) egyenlőtlenség? (3 pont)

B. 3564. Vigyük át az (x,y) koordináta-sík A(0;1) pontját a B(3;2) pontba az x-tengelyre való tükrözések és az A pont körüli elforgatások alkalmazásával. (4 pont)

B. 3565. Adott 2002 doboz, mindegyikükben néhány kavics. Ezen kívül korlátlan számú kavics áll rendelkezésünkre. Egy lépésben bármely k dobozba betehetünk 1-1 kavicsot. Elérhető-e, hogy bizonyos számú lépés után minden egyes dobozban ugyanannyi kavics legyen, ha

a) k=8

b) k=9? (4 pont)

B. 3566. Az ABC háromszögről tudjuk, hogy minden P belső pontjára a PA, PB és PC szakaszokból háromszög szerkeszthető. Mutassuk meg, hogy az ABC háromszög szabályos. (4 pont)

B. 3567. Egy konvex ötszögről tudjuk, hogy minden oldala párhuzamos valamelyik átlójával. Mekkora lehet egy oldal és a vele párhuzamos átló hosszának aránya? (5 pont)

B. 3568. Mely \(\displaystyle alpha\) szögetre igaz, hogy minden k nemnegatív egészre cos2^k0? (5 pont)

B. 3569. 100 kockáról tudjuk, hogy bármelyik kettőnek van közös belső pontja, és a kockák élei három adott egyenes valamelyikével párhuzamosak. Mutassuk meg, hogy ekkor az összes kockának van közös pontja.

Adjunk meg 100 kockát úgy, hogy közülük bármely háromnak legyen közös belső pontja, de ne legyen olyan pont, amelyik mindegyik kockában benne van. (5 pont)

B. 3570. A folytonos f függvényre teljesül, hogy f(1000)=999 és f(x)^.f(f(x))=1 minden valós x számra. Határozzuk meg f(500) értékét. (4 pont)

B. 3571. Egy egyenes csonkakúp alakú poharat körbegurítottunk egy kör alakú asztalon úgy, hogy mozgás közben sosem érte el az asztal peremét. Az asztal átmérője 1,6 m. A pohár alja 5 cm, a teteje pedig 6,5 cm átmérőjü kör. Milyen magas lehet a pohár? (4 pont)

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 296. András gondolt egy 16-nál nem nagyobb pozitív egészre. Béla feltehet 7 eldöntendő kérdést, amelyre András igennel vagy nemmel válaszolhat, és egyszer rossz választ is adhat. Segítsünk Bélának kitalálni a gondolt számot.

Cseh versenyfeladat

A. 297. Legyenek a₀,a₁,a₂,... pozitív egészek úgy, hogy a₀=1, a₁>1 és

\(\displaystyle a_{n+1}=\frac{a_1\cdot\ldots\cdot a_n}{a_{[n/2]}}+1\)

teljesül minden n=1,2,... esetén. ([x] jelöli az x egész részét.) Mutassuk meg, hogy a

\(\displaystyle \sum_{n=1}^\infty\frac{1}{a_{n+1}a_{[n/2]}}\)

sor összege egy racionális szám.

Cseh versenyfeladat

A. 298. Egy gömbháromszög szögei , , , a velük szemközti oldalívek hossza a, b, illetve c. Igazoljuk, hogy

a^.cos\(\displaystyle beta\)+b^.cos<c.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2002. október 15.