A 2002. októberi számban kitűzött fizika elméleti feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

P. 3551. Egy egyenáramú játékmotorral hajtott daru 0,2 m/s sebességgel emel fel egy 200 g tömegű terhet. Mekkora teljesítményű villanymotorral dolgozik a daru, ha a teljes munkavégzés 10%-a a súrlódások legyőzésére fordítódik? Mekkora a 9 V-os villanymotor áramfelvétele, ha a hatásfoka 80%? (3 pont)

Közli: Holics László, Budapest

Megoldás. A motor teljesítménye 0,44 W, áramfelvétele pedig 0,06 A.

P. 3552. Egy kút mélységét annak alapján akarjuk meghatározni, hogy mennyi idő múlva halljuk a beejtett kő csobbanását. Mekkora hibával tudjuk meghatározni a kút mélységét, ha időmérésünk hibája p%? A légellenállást és a hang terjedésének idejét hanyagoljuk el! Mikor jogos ez az elhanyagolás? (4 pont)

Közli: Radnai Gyula, Budapest

Megoldás. A mélységmérés relatív hibája

\(\displaystyle {\Delta s\over s}=2{\Delta t\over t}=(2p)\%\,.\)

A közegellenállás és a hangterjedés véges idejének elhanyagolása akkor jogos, ha az eső kő végsebessége nem túl nagy, azaz a kút nem túl mély. A légellenállás elhanyagolásából származó hiba - adott mélységű kút esetén - olymódon csökkenthető, hogy nagyobb méretű követ ejtünk a kútba.

P. 3553. Összegezzük az F és kF nagyságú erőket, melyek egymással \(\displaystyle \alpha\) szöget zárnak be (k\(\displaystyle \ge\)1). Az \(\displaystyle \alpha\) szög mely értékénél lesz az eredőnek a kF összetevővel alkotott \(\displaystyle \varepsilon\) szöge a legnagyobb? Mekkora ez a szög?

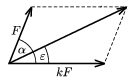
(4 pont)

Vermes Miklós feladata

Megoldás.

\(\displaystyle {\rm tg}\,\varepsilon={\sin\alpha\over k+\cos\alpha},\)

ez akkor a legnagyobb, ha cos \(\displaystyle \alpha\)=-1/k. Ilyenkor

\(\displaystyle {\rm tg}\,\varepsilon={1\over\sqrt{k^2-1}}.\)

P. 3554. Egy tömör golyót és egy tömör hengert egyszerre engedünk el egy lejtő tetejéről. Lehetséges-e, hogy egyszerre érnek le a lejtő aljára? Milyen esetekben? (5 pont)

Közli: Kovács Tamás, Budapest

Megoldás. A mozgásegyenlet

mgsin \(\displaystyle \alpha\)-S=ma.

Tiszta gördülés esetén

\(\displaystyle Sr=\Theta\beta\) és r\(\displaystyle \beta\)=a,

azaz

\(\displaystyle a={g\sin\alpha\over1+\left(\Theta/mr^2\right)}.\)

Mivel \(\displaystyle \Theta/mr^2\) alakfüggő, a is az, tehát tiszta gördülés esetén a golyó és a henger biztos nem egyszerre ér le. Ha a guruló test köszörül (csúszik és gurul)

S=\(\displaystyle \mu\)mgcos \(\displaystyle \alpha\)

és

a=gsin \(\displaystyle \alpha\)(1-\(\displaystyle \mu\) ctg \(\displaystyle \alpha\)),

ekkor tehát egyszerre ér le a golyó és a henger. A köszörülés feltétele

\(\displaystyle \beta={Sr\over\Theta}={r\mu mg\cos\alpha\over\Theta}< {a\over r}={g\sin\alpha(1-\mu\,{\rm ctg}\,\alpha)\over r} \)

azaz

\(\displaystyle \mu<{{\rm tg}\,\alpha\over1+\left(mr^2/\Theta\right)}. \)

\(\displaystyle mr^2/\Theta\) gömbre 5/2, míg hengerre csak 2, így a szigorúbb feltétel

\(\displaystyle \mu<{2\over7}\,{\rm tg}\,\alpha.\)

P. 3555. Egy fal előtt állunk. Köztünk és a fal között fülünk magasságában síp szól, amelynek rezgésszáma 600 Hz. Milyen sebesen kell mozgatni a sípot a fal felé, hogy másodpercenként 3 lebegést halljunk? (4 pont)

Kurucz László feladata nyomán

\(\displaystyle v=\frac{\sqrt{f_0^2+\Delta f^2}-f_0}{\Delta f}\,c=86~\rm cm/s.\)

(Itt f₀ a síp hangjának, \(\displaystyle \Delta\)f pedig a lebegés frekvenciája, és c a hangsebesség.)

P. 3556. Toroid tekercs légrésében homogénnek tekinthető, kör keresztmetszetű mágneses mező jön létre. Az erővonalakra merőlegesen, sugár irányban belépő töltött részecskék közül a nagyobb vagy a kisebb sebességűek hagyják el hamarabb a mágneses mezőt?

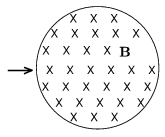
(5 pont)

Közli: Varga István, Békéscsaba

Megoldás. Az adott mágneses térben a v sebességű elektron pályájának a sugara

\(\displaystyle r={vm\over eB}\,, \)

és egy teljes kör befutásához szükséges idő

\(\displaystyle T={2\pi m\over eB}\,. \)

Ez független a sebességtől, tehát a mágneses mezőben töltött idő a befutott körívhez tartozó középponti szöggel arányos. Eszerint a gyorsabb elektronok hagyják el hamarabb a mágneses mezőt.

P. 3557. Derékszögű, szimmetrikus üvegprizma átfogójára monokromatikus fénysugár esik a levegőből. Az \(\displaystyle \alpha\) beesési szöget válasszuk meg úgy, hogy a másik két lapon teljes visszaverődés jöjjön létre (n=1,5).

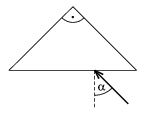
a) Határozzuk meg a prizmába belépő és az abból kilépő fénysugarak által bezárt szöget!

b) Legfeljebb mekkorának választhatjuk az \(\displaystyle \alpha\) beesési szöget, hogy a teljes visszaverődések bekövetkezzenek? (5 pont)

Közli: Kotek László, Pécs

Megoldás. a) A belépő és kilépő sugarak párhuzamosak.

b) Az \(\displaystyle \alpha\) beesési szögnek \(\displaystyle \pm\)4,8^o közé kell esnie.

P. 3558. Az atomreaktorokban a lassú, termikus neutronok nagyobb valószínűséggel hoznak létre maghasadást, mint a gyors neutronok; ezért a hasadáskor képződő neutronokat nehézvízzel vagy grafittal fékezik (moderálják).

Határozzuk meg, hogy energiájának hány százalékát veszíti el a neutron, ha álló ²₁H, illetve \(\displaystyle {}^{12}_{\phantom{1}6}\rm C\) atommaggal ütközik egyenesen, rugalmasan! (4 pont)

Bakonyi Gábor feladata nyomán

Megoldás. A maghasadások során felszabaduló neutronok mozgási energiája MeV nagyságrendű, vagyis sokkal kisebb, mint a neutron mc²\(\displaystyle \approx\)1 GeV nagyságú nyugalmi eneriája, ezért számolhatunk a klasszikus (nemrelativisztikus) newtoni fizika törvényeivel.

A v sebességű m₁ tömegű részecske sebessége az álló m₂ tömegű részecskével való centrális ütközés után

\(\displaystyle u=v{m_1-m_2\over m_1+m_2},\)

ennek megfelelően a mozgási energiájának

\(\displaystyle 1-\left({u\over v}\right)^2={4m_1m_2\over\left(m_1+m_2\right)^2}\)

hányadát veszíti el az ütközés során. Ez a feladatban adott két esetben (m₂=2m₁, illetve m₂=12m₁) 88,9%, illetve 28,4%.

P. 3559. Adjunk becslést arra, hogy Magyarország területének hány százalékát kellene modern (50% hatásfokú) napelemekkel beborítani, hogy fedezni lehessen az ország jelenlegi teljes villamos teljesítmény szükségletét, ami átlagosan 7 GW! (5 pont)

Közli: Honyek Gyula, Budapest

Megoldás. A Magyarország területét érő napsugárzás átlagos tejesítménye

\(\displaystyle L=JA{n_1\over n_2}\overline{\cos\phi}= 8{,}6\cdot10^{12}~{\rm W}.\)

Itt J\(\displaystyle \approx\)1 kW/m² a földfelszínt elérő energia-áramsűrűség, A=94^.10⁹ m² Magyarország területe, n₁ a napsütéses órák száma, ennek becsült értéke 2000, n₂=8760 az év hossza órában kifejezve, \(\displaystyle \phi\) a sugárzás beesési szöge \(\displaystyle \overline{\cos\phi}\) pedig a cos \(\displaystyle \phi\) átlaga, amit 0,4-nek becsültünk. Ennek a kivánt 7^.10⁹ W a 0,08%-a, tehát 50% hatásfokú energiaátalakítás esetén az ország területének 0,16%-át kellene napelemekkel beborítani.

P. 3560. Egy 1 m hosszú, egyik végénél mereven befogott vízszintes pálca másik végére 1 kg tömegű testet akasztva a lehajlás 1 cm lesz. Becsüljük meg, hogy függőlegesre állítva mekkora F terhelés hatására hajlik ki ez a pálca.

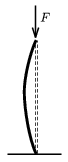
(Útmutatás: Egy meghajlított pálca rugalmas energiája egyenesen arányos a hosszával és fordítottan arányos a görbületi sugár négyzetével.) (6 pont)

Közli: Gnädig Péter, Budapest

Megoldás. Ha G súly hatására az L hosszú vízszintes pálca lehajlása h, akkor a függőleges terhelés kritikus értéke közelítőleg

\(\displaystyle F_{\rm kritikus}\approx3G\,\frac{L}{h}\approx3000~\rm N.\)