Matematikából kitűzött gyakorlatok és feladatok
2002. november

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok

Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 690. Lehet-e három egész élhosszúságú kocka térfogatának az összege 2002 egység?

C. 691. Hány mm² Magyarország területe egy 25 cm átmérőjű földgömbön?

C. 692. Az x, y, z valós számokra teljesül, hogy x+2y+4z $\ge$ 3 és y-3x+2z$\displaystyle \ge$5. Igazoljuk, hogy ekkor y-x+2z$\displaystyle \ge$3.

C. 693. Mekkora lehet egy olyan egyenlő szárú háromszög szárszöge, amelynek magasságaiból mint oldalakból háromszög szerkeszthető?

C. 694. Mekkora az [log₂1]+[log₂2]+[log₂3]+...+[log₂2002] összeg értéke?

Javasolta: Besenyei Ádám, Budapest

A B pontversenyben kitűzött feladatok

A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3582. Oldjuk meg a természetes számok körében a

3xyz-5yz+3x+3z=5

egyenletet. (3 pont)

B. 3583. Egy ABC háromszög beírt körének középpontját összekötöttük a háromszög csúcsaival. Az így kapott háromszögek közül az egyik hasonló az ABC háromszöghöz. Mekkorák az ABC háromszög szögei? (3 pont)

B. 3584. Írjuk le az egész számokat egyesével 1-től 10^n-1-ig, és legyen az eközben leírt számjegyek száma A. Ezek után ismét írjuk le az egész számokat egyesével, ezúttal 1-től 10ⁿ-ig, és legyen az így leírt nullák száma B. Bizonyítsuk be, hogy A=B. (4 pont)

B. 3585. Határozzuk meg az a paraméter azon értékeit, amelyekre az

$\displaystyle \sqrt{1+x^4$1-2ax+x^2">

egyenlőtlenség minden pozitív x-re teljesül. (3 pont)

XI. Nemzetközi Magyar Matematika Verseny

B. 3586. Az a paraméter mely értékeire van a lg(ax)=2lg(x+1) egyenletnek pontosan egy megoldása? (4 pont)

B. 3587. Adott gömb köré négyzet alapú, egyenes csonkagúlát írunk. Mekkora lehet a csonkagúla térfogatának és felszínének az aránya? (4 pont)

B. 3588. Adott egy kör és a belsejében az M pont. Egy M csúcsú derékszög szárai a kört az A és B pontokban metszik. Mi az AB szakasz felezőpontjának mértani helye, ha a derékszög körbefordul az M pont körül? (4 pont)

B. 3589. Bizonyítsuk be, hogy végtelen sok olyan n páratlan pozitív egész szám létezik, amelyre 2ⁿ+n összetett szám. (4 pont)

B. 3590. Az x³-10x+11=0 egyenlet gyökei u, v és w. Határozzuk meg az

arctg u+arctg v+arctg w

értékét. (5 pont)

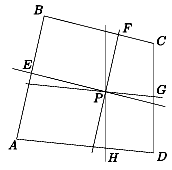
B. 3591. A konvex ABCD négyszög területe T, egy belső pontja P. A P-n keresztül BC-vel húzott párhuzamos egyenes a BA oldalt az E, az AB-vel húzott párhuzamos egyenes a BC oldalt az F, az AD-vel húzott párhuzamos egyenes a CD oldalt a G pontban, a CD-vel húzott párhuzamos egyenes az AD oldalt a H pontban metszi. Jelölje az AEPH négyszög területét t₁, a PFCG négyszög területét t₂. Bizonyítsuk be, hogy 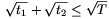$\sqrt{t_1}+\sqrt{t_2}\leq\sqrt{T}$ .