Matematikából kitűzött gyakorlatok és feladatok
2003. január

Kérjük, olvassa el a versenykiírást.

A C pontversenyben kitűzött gyakorlatok Minden C-jelű feladat helyes megoldásáért 5 pont jár.

C. 700. Papírból kivágunk egy négyszög alakú lapot, ráírjuk üdvözlő sorainkat, majd sarkainál behajtjuk úgy, hogy a csúcsok egy közös pontba kerüljenek. Milyen négyszöget vágjunk ki, hogy a behajtott részek hézagmentesen és egymás átfedése nélkül takarják a négyszög többi részét?

C. 701. Mutassuk meg, hogy 1^.2 ^....^.1001+ 1002 ^.1003^....^.2002 osztható 2003-mal.

C. 702. Egy derékszögű háromszög hegyesszögei 60^o és 30^o. A háromszögbe két egyenlő sugarú kört írunk, amelyek érintik az átfogót, egymást és egy-egy befogót. Hányszorosa a kisebbik befogó a körök sugarának?

C. 703. A p valós paraméter értékétől függően hány gyöke van a

2x²-10px+7p-1=0

egyenletnek a (-1;1) intervallumban?

C. 704. Mely n természetes számokra igaz, hogy

log₂3 ^.log₃4 ^.log₄5 ^....^.log_n(n+1)=10?

A B pontversenyben kitűzött feladatok A B-jelű feladatokra kapható pontszám a feladatok nehézségétől függ. Minden hónapban a 6 legnagyobb pontszám számít be a pontversenybe.

B. 3602. A négyzet alakú medencében úszkáló Jerry el szeretne menekülni a parton rá leső Tom elől. Tom nem tud úszni, lassabban fut, mint Jerry, viszont négyszer olyan gyorsan fut, mint ahogy Jerry úszik. Megmenekülhet-e mindig Jerry?

(5 pont)

B. 3603. Szerkesszünk adott háromszög belsejében olyan pontot, melynek a háromszög oldalegyeneseitől való távolságainak aránya 1:2:3.

(3 pont)

B. 3604. Az x, y valós számokra teljesül, hogy x+y=1. Határozzuk meg az A(x,y)=x⁴y+ xy⁴+ x³y+ xy³+ x²y+ xy² kifejezés legnagyobb értékét.

(3 pont)

B. 3605. Az ABC háromszög CA oldalának A-n túli meghosszabbításán adott a D pont, a CB oldalának B-n túli meghosszabbításán pedig az E pont úgy, hogy AB=AD=BE. Az ABC háromszög A-ból és B-ből induló szögfelezői a szemközti oldalakat az A₁ illetve a B₁ pontokban metszik. Mekkora az ABC háromszög területe, ha a DCE háromszög területe 9 egység, az A₁CB₁ háromszög területe pedig 4 egység?

(3 pont)

Javasolta: Bakonyi Gábor, Budapest

B. 3606. Adjunk meg olyan a és b egész számokat, amelyekre teljesül, hogy .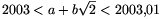

(3 pont)

B. 3607. Egy konvex négyszög szemközti oldalegyenesei metszik egymást. Megrajzoljuk a metszéspontoknál keletkezett szögek belső szögfelezőit. Bizonyítsuk be, hogy a négyszög akkor és csak akkor húrnégyszög, ha e két szögfelező merőleges egymásra, és ebben az esetben a szögfelezők a négyszög oldalait egy rombusz csúcsaiban metszik.

(4 pont)

Javasolta: Rácz János, Budapest

B. 3608. Adjuk meg azoknak az a, b, c számoknak a tízes számrendszerbeli alakját, amelyekre az x³+ax²+bx+c=0 egyenlet gyökei rendre egyenlők az x³-3x+1=0 egyenlet három gyökének az ötödik hatványával.

(4 pont)

B. 3609. Van-e olyan f(x) egész együtthatós 2003-ad fokú polinom, amelyre bármely n egész szám esetén az

f(n), f(f(n)), f(f(f(n))), ...

értékek páronként relatív prímek?

(5 pont)

B. 3610. Bizonyítsuk be, hogy

sin 25^o.sin 35^o.sin 60^o.sin 85^o=sin 20^o.sin 40^o.sin 75^o.sin 80^o.

(5 pont)

B. 3611. Az x_n+1=x_n²-x_n+1 rekurzióval definiált sorozat elemeiből készítsük el a 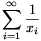végtelen sort. Mennyi ennek a sornak az összege, ha a) x₁=1/2; b) x₁=2?

(5 pont)

Az A pontversenyben kitűzött nehezebb feladatok Minden A-jelű feladat helyes megoldásáért 5 pont jár.

A. 308. Az A, B, C, D, E pontok úgy helyezkednek el a síkban, hogy AB=BC=CD=DA=1, és AE, BE, CE és DE mindegyike legfeljebb 1. Legfeljebb mekkora lehet AE+BE+CE+DE+AC+BD?

A. 309. Egy n csúcsú egyszerű gráfban a csúcsok fokszámai rendre 0<d₁...d_n. Bizonyítsuk be, hogy kiválasztható legalább \(\displaystyle \sum\frac{2}{d_i+1}\) csúcs úgy, hogy az általuk kifeszített részgráfban nincs kör.

A. 310. Legyen tetszőleges n pozitív egészre

\(\displaystyle s_n(x)=\sum_{d\mid n}\frac{n}{d}x^d,\)

és definiáljuk a p₀,p₁,... polinomokat a következő rekurzióval: p₀(x)=1,

\(\displaystyle p_n=\frac{1}{n}\sum_{k=1}^ns_k(x)p_{n-k}(x).\)

Igazoljuk, hogy a p_n polinom mindegyik együtthatója egész szám.

A matematika gyakorlatok és feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2003. február 15.