Fizikából kitűzött gyakorlatok és feladatok
2003. február

Kérjük, olvassa el a versenykiírást.

Mérési feladat

M. 240. Optikai rács felhasználásával tanulmányozzuk különböző LED-ek (fénykibocsátó diódák) fényének monokromatikusságát: határozzuk meg, milyen tartományba esik a kibocsátott fény hullámhossza!

(6 pont)

Közli: Varga István, Békéscsaba

Az elméleti versenyben kitűzött gyakorlatok és feladatok Az elméleti fizika feladatokra kapható pontszám a feladatok nehézségétől függ. Az 1-8. osztályosok versenyében minden hónapban a 3 legnagyobb, a 9-12. osztályosok versenyeiben minden hónapban az 5 legnagyobb pontszám számít be a pontversenybe.

P. 3591. Egy metróállomás 3,5 m széles kijáratán percenként átlagosan 70 ember halad át azonos irányban. A ,,népsűrűség'' 0,4 fő/m².

Mekkora az emberek átlagos sebessége?

(3 pont)

Közli: Varga Zsuzsa, Szeged
Tarján Imre emlékverseny, Szolnok

P. 3592. Galvánelemből, akkumulátorból és egy ohmos ellenállásból összeállított elágazás nélküli áramkörben az akkumulátoron és az ellenálláson is 9 V feszültség mérhető.

Mekkora feszültség mérhető az ugyancsak 9 V-os, de nem zérus belső ellenállású galvánelemen, és mit állapíthatunk meg az ellenállás nagyságáról?

(4 pont)

Közli: Radnai Gyula, Budapest

P. 3593. Egy vízszintes síkú, R sugarú mágneskorong \(\displaystyle \omega\)₀ szögsebességgel forog a középpontján átmenő, rögzített függőleges tengely körül. Kis magasságból ráesik egy ugyanilyen, kezdetben nyugvó korong, és azonnal hozzátapad. (A két korong középpontja R-nél kisebb távolságra lesz egymástól.)

Mekkora közös szögsebességgel fog forogni a két korong?

(4 pont)

Közli: Simon Péter, Pécs

P. 3594. Fonálingát derékszögben kitérítünk, majd lökés nélkül elengedjük. Az ábra szerinti AP vagy PB szakaszt teszi meg az inga rövidebb idő alatt?

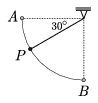
(5 pont)

Közli: Károlyházy Frigyes, Budapest
Mikola Sándor fizikaverseny, Gyöngyös

P. 3595. Félgömb alakú mélyedést hozunk létre egy hasáb belsejében. Az M tömegű hasáb a vízszintes asztalon szabadon elmozdulhat. A nyugvó hasáb P pontjánál elengedünk egy m tömegű pontszerű testet. Mekkora erővel nyomja a hasáb a kis testet a \(\displaystyle \varphi\) szögű helyzetben? (A súrlódás mindenütt elhanyagolható.)

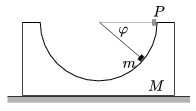
(5 pont)

Közli: Pálfalvi László, Pécs

P. 3596. Egy 3 literes tartályban 2,2^.10⁶ Pa nyomású és 80 ^oC hőmérsékletű, egy 5 literesben pedig 1,3^.10⁵ Pa nyomású és 5 ^oC-os oxigéngáz van. A két tartályt egy rövid csővel összekötjük. Mekkora lesz bennük a közös nyomás akkor, amikor a gáz felveszi a szoba 23 ^oC-os hőmérsékletét? Mennyi gáz áramlott át eközben a csövön?

(4 pont)

Közli: Hilbert Margit, Szeged
Tornyai Sándor fizikaverseny, Hódmezővásárhely

P. 3597. Bizonyos mennyiségű nemesgáz állapotváltozása során Q hőt vesz fel, miközben térfogata V₁-ről V₂-re nő, nyomása térfogatával arányosan növekszik. Mekkora V₃ térfogatra tágulna ki a gáz a kezdeti V₁ térfogatról, ha úgy venne fel Q hőt, hogy nyomása mindvégig a kezdeti értéken maradna?

(Adatok: V₁=5 dm³, V₂=8 dm³.)

(4 pont)

Közli: Légrádi Imre, Sopron

P. 3598. Vákuumban elhelyezett síkkondenzátor A területű fémlemezei vízszintes szigetelő szálon súrlódásmentesen csúszhatnak. A bal oldali lemez tömege m, töltése Q, a jobb oldali lemez tömege 2m, töltése -2Q. A lemezek kezdetben rögzítettek, távolságuk 3d.

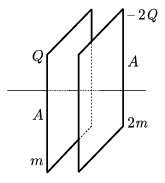
a) Mekkora a lemezek közötti elektromos mező energiája?

b) Egy adott pillanatban a lemezek rögzítését megszüntetjük. Mekkora lesz a lemezek sebessége akkor, amikor távolságuk már csak d?

(5 pont)

Közli: Kotek László, Pécs
Párkányi László fizikaverseny, Pécs

P. 3599. Debrecenben 1984-ben méréssel megállapították, hogy a maghasadás egyik lehetséges termékeként keletkező ⁸⁵Kr izotóp \(\displaystyle \beta\)^- bomlásának aktivitás-koncentrációja 0,8 Bq/m³. Becsüljük meg, hány kg kripton bomlik el óránként a légkörben?

(5 pont)

Közli: Kopcsa József, Debrecen

P. 3600. Két nagyméretű, földelt fémlap \(\displaystyle \alpha\) szöget zár be egymással. A szögfelező síkban, a síkok metszésvonalától r távolságban egy L hosszúságú (L\(\displaystyle \gg\)r), egyenletesen elosztott Q töltésű, vékony pálca található. Mekkora erő hat a pálcára az elektromos megosztás következtében, ha

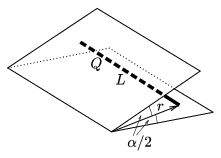
a) \(\displaystyle \alpha\)=180^o,

b) \(\displaystyle \alpha\)=18^o.

(5 pont)

Közli: Gnädig Péter, Budapest

A fizika feladatok megoldásai a következő címekre küldhetők:

KöMaL Szerkesztőség
Budapest 112, Pf. 32.  1518

megoldas@komal.hu (Az interneten keresztül történő beküldésről olvassa el tájékoztatónkat)

A beküldési határidő: 2003. március 11.