A számítástechnika-versenyben kitűzött feladatok 2003. február

Kérjük, olvassa el a versenykiírást.

I. 43. Írjunk programot (i43.pas,...), amely adott célértékre (2 \(\displaystyle \le\)CEL \(\displaystyle \le\)10 000 000) megadja azt a legnagyobb n értéket, amelyre

F(n-1)^.x+F(n)^.y=CEL,

ahol F(n) az n-edik Fibonacci szám x és y nem negatív egészek.

(10 pont)

I. 44. Készítsünk programot (i44.pas,...), amely egy ellipszist forgat az origó (a képernyő középpontja) körül időegységenként ALFA szöggel úgy, hogy közben az ellipszis is forog a saját középpontja körül időegységenként BETA szöggel. Az ellipszist nagytengelye és kistengelye hosszával adjuk meg. Kezdetben az ellipszis középpontja a képernyő középső sorában van, a maximális sorszámú oszlop háromnegyedénél. A program tetszőleges időegységig működjön, minden időegység végén rajzolja az ábrát!

Példa: ALFA=60, BETA=70, NAGYTENGELY=50, KISTENGELY=25

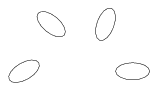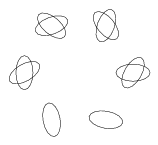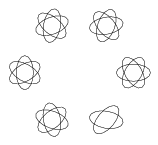1. rajz		4. rajz		10. rajz		17. rajz

(10 pont)

I. 45. Egy 100x100-as táblázathoz mintákat generálhatunk, ha kiszámoljuk egyes transzformált pontjai távolságnégyzetét a (0,0) koordinátájú ponttól, a távolságot egészre kerekítjük, majd páros szám esetén fekete, páratlan esetén pedig fehér színt rendelünk hozzá. A transzformáció az (x,y) pontot (dx,dy)-szorosra nyújtja, majd (sx,sy)-nal eltolja.

Készítsünk táblázatot (i45.xls), amely a második munkalapon található dx, dy, sx, sy alapján az első munkalapon egy 100x100-as mintázatot alakít ki.

Példa:

dx=0,25, dy=0,25, sx=0, sy=0	dx=0,25, dy=0,25, sx=10, sy=20	dx=0,1, dy=0,1, sx=50, sy=50

A számítástechnike feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2003. március 13.