 |
A 2003. márciusi C-jelű matematika gyakorlatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
C. 710. Egy iskolában a diákok átlagéletkora 16 év, a tanároké 38 év, az összes diák és tanár átlagéletkora együtt 17 év. A tanárok átlagosan 21 órát tanítanak hetente, a diákoknak pedig hetente átlagosan 29 órájuk van. Minden osztálynak ugyanannyi a létszáma. Hány gyerek jár egy osztályba ebben az iskolában?
Megoldás. A diákok összlétszámát d-vel, a tanárokét t-vel jelölve az átlagéletkorokra teljesülő feltételek miatt 16d+38t=17(d+t), azaz d=21t. Az osztályok közös létszáma legyen l; ekkor 21tl=29d=29.21t, ahonnan l=29.
C. 711. Egy pozitív számokból álló sorozat bármely három egymás utáni elemére teljesül, hogy a középső szám a két szélsőnek a szorzata. Az első öt elem, valamint az utána következő öt elem szorzata is 2. Határozzuk meg a sorozat első tíz tagját.
Megoldás. A harmadiktól kezdve a sorozat minden eleme az előtte levőnek és az azt megelőzőnek a hányadosa. Így, ha az első elem a, a második pedig b, akkor az első tíz elem a következő:\(\displaystyle a,b,{b\over a},{1\over a},{1\over b},{a\over b},a,b,{b\over a},{1\over a}.\)
Az első öt elem szorzata \(\displaystyle 2=a\cdot b\cdot{b\over a}\cdot{1\over a}\cdot{1\over b}={b\over a}\), a második öt elem szorzata \(\displaystyle 2={a\over b}\cdot a\cdot b\cdot{b\over a}\cdot{1\over a}=b\), tehát b=2 és a=1. A sorozat első tíz tagja:
\(\displaystyle 1,2,2,1,{1\over2},{1\over2},1,2,2,1.\)
C. 712. Az ABC háromszögben a szokásos jelölésekkel \(\displaystyle \gamma\)=3\(\displaystyle \alpha\), a=27, c=48. Határozzuk meg a b oldal hosszát.
Megoldás. sin\(\displaystyle gamma\)=sin3\(\displaystyle alpha\)=3sin\(\displaystyle alpha\)-4sin3\(\displaystyle alpha\); a szinusztétel szerint\(\displaystyle 3-4\sin^2\alpha={\sin\gamma\over\sin\alpha}={c\over a}={16\over9},\)
így \(\displaystyle \sin\alpha={\sqrt{11}\over6}\), \(\displaystyle \cos\alpha={5\over6}\), \(\displaystyle \sin\gamma={8\sqrt{11}\over27}\), \(\displaystyle \cos\gamma=-{5\over27}\), \(\displaystyle \sin\beta=\sin(\alpha+\gamma)=\sin\alpha\cos\gamma+\cos\alpha\sin\gamma={35\sqrt{11}\over6\cdot27}\). Tehát a szinusztétel alapján
\(\displaystyle b=c{\sin\beta\over\sin\gamma}=48\cdot{35\sqrt{11}\over6\cdot27}\cdot{27\over8\sqrt{11}}=35.\)
C. 713. Hány megoldása van a [0;2\(\displaystyle \pi\)] intervallumban a
sin 2002x=sin 2003x
egyenletnek?
Megoldás. Az egyenlet valós megoldásai azok az x számok, amelyekre 2003x-2002x=2k\(\displaystyle pi\) vagy 2003x+2002x=(2k+1)\(\displaystyle pi\), ahol k egész. Az első feltételt [0,2\(\displaystyle pi\)]-ben a 0 és a 2\(\displaystyle pi\) elégíti ki. A másik megoldássereg -- \(\displaystyle x={2k+1\over4005}\pi\) -- [0,2\(\displaystyle pi\)]-be eső értékei:\(\displaystyle {1\over4005}\pi,{3\over4005}\pi,{5\over4005}\pi,\ldots,{8009\over4005}\pi,\)
ez 4005 darab szám. Összesen tehát a megoldások száma 4007.
C. 714. Egy tó vizében egy ottfelejtett labda úszott. A téli fagy beköszöntével a tó fenékig befagyott, a labdát kiemelték, és egy 8 cm mély, 24 cm átmérőjű mélyedés maradt a nyomában. Hány centiméter a labda sugara?
Megoldás.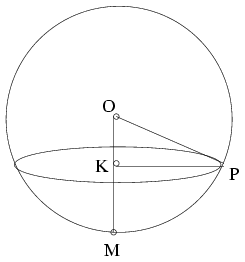
Jelölje a labda középpontját O, a mélyedés szélét alkotó kör középpontját K, a kör egy tetszőleges pontját P, a mélyedés legalsó pontját pedig M. Ha a labda sugara r, akkor Pitagorasz tétele szerint OP2=OK2+KP2, azaz r2=(r-8)2+122, amiből a labda sugara r=13 cm.

