A 2003. szeptemberi B-jelű matematika feladatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

A B. 3652. feladat tanulságai

B.3653.

(3 pont)

Megoldás: A négyzet oldalegyenesei a síkot 9 tartományra osztják, melyek közül egyik maga a négyzet, 4 egybevágó végtelen tartomány a négyzet egy-egy oldalára illeszkedik, míg a másik 4 végtelen tartomány a négyzet egy-egy csúcsára. A keresett pontok csak a négyzeten kívül helyezkedhetnek el, és szimmetria okok miatt elegendő a két különböző típusú végtelen tartományból egyet-egyet megvizsgálni. Ha T az ABCD négyzet AB oldalára illeszkedő végtelen tartomány, akkor T pontjaiból a négyzet pontosan olyan szög alatt látszik, mint maga az AB oldal. Ezért a keresett pontok egy, az AB szakasz fölé emelt 30^o-os látóköríven helyezkednek el, melynek minden T-be eső pontja megfelelő lesz. A keresett mértani hely T-be eső része tehát az ABXY körvonal XY íve, ahol az X és Y pontok a CB, illetve DA félegyenesek azon pontjai, melyekre \(\displaystyle BX=AY=\sqrt{3}AB\).

Hasonlóképpen, ha S a négyzet B csúcsára illeszkedő végtelen tartomány, akkor S pontjaiból a négyzet éppen akkora szög alatt látszik, mint az AC átló, így a mértani hely S-be eső része éppen az AC szakaszra emelt egyik 30^o-os látókörív S-sel alkotott metszete lesz. Mivel az X pont az S és T tartományokhoz is hozzátartozik, az ív egyik végpontja éppen az X pont lesz, másik végpontja pedig szimmetria okok miatt az AB félegyenesnek azon Z pontja, melyre \(\displaystyle BZ=\sqrt{3}AB\).

A teljes mértani helyet úgy kapjuk, hogy az említett XY és XZ íveket a négyzet középpontja körül elforgatjuk 90^o-kal, 180^o-kal és 270^o-kal is. A mértani hely az így keletkezett 8 körív uniója.

B.3654.

(3 pont)

Megoldás: Ha a k egész szám 3-mal osztva 0 vagy 2 maradékot ad, akkor k²+k=k(k+1) osztható 3-mal. Ha k=3\(\displaystyle \ell\)+1, akkor

k²+k=(9\(\displaystyle \ell\)²+6\(\displaystyle \ell\)+1)+(3\(\displaystyle \ell\)+1)=9(\(\displaystyle \ell\)²+\(\displaystyle \ell\))+2

mind 3-mal, mind 9-cel osztva 2 maradékot ad. Ebből azonnal látszik, hogy az A=(m²+m)+(n²+n)-1 szám csak úgy lehet 3-mal osztható, ha m és n egyaránt 1 maradékot ad 3-mal osztva. Ekkor viszont A 9-cel osztva 3 maradékot ad, vagyis semmilyen esetben nem lehet 9-cel osztható.

B.3655.

(4 pont)

Megoldás: Legyen az O középpontú kör sugara egységnyi és jelölje az a,b,c húrokhoz tartozó kerületi szögeket rendre \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\), ekkor 2\(\displaystyle \alpha\)+2\(\displaystyle \beta\)+2\(\displaystyle \gamma\)=\(\displaystyle \pi\). Az OAB és OBC egyenlő szárú háromszögek alapja a=2sin \(\displaystyle \alpha\), magassága pedig cos \(\displaystyle \alpha\), ezért ezen háromszögek területe külön-külön sin \(\displaystyle \alpha\)cos \(\displaystyle \alpha\)-val egyenlő. Ugyanígy kapjuk, hogy az OCD és ODE háromszögek területe sin \(\displaystyle \beta\)cos \(\displaystyle \beta\), az OEF és OFA háromszögeké pedig sin \(\displaystyle \gamma\)cos \(\displaystyle \gamma\).

A BOD szög nagysága 2\(\displaystyle \alpha\)+2\(\displaystyle \beta\), ahonnan a BOD egyenlő szárú háromszög területe sin (\(\displaystyle \alpha\)+\(\displaystyle \beta\))cos (\(\displaystyle \alpha\)+\(\displaystyle \beta\))=cos \(\displaystyle \gamma\)sin \(\displaystyle \gamma\). Ugyanígy a DOF és FOB háromszögek területe rendre cos \(\displaystyle \alpha\)sin \(\displaystyle \alpha\) és cos \(\displaystyle \beta\)sin \(\displaystyle \beta\). Mivel a BOD, DOF, FOB szögek összege éppen 2\(\displaystyle \pi\), az O pont a BDF háromszög belsejében helyezkedik el. Ezért a BDF háromszög területe,

sin \(\displaystyle \alpha\)cos \(\displaystyle \alpha\)+sin \(\displaystyle \beta\)cos \(\displaystyle \beta\)+sin \(\displaystyle \gamma\)cos \(\displaystyle \gamma\)

éppen fele az OAB, OBC, OCD, ODE, OEF, OFA háromszögek együttes területének. Lévén O az ABCDEF hatszög belső pontja, ez utóbbi összeg megegyezik a hatszög területével. Ezzel az állítást igazoltuk.

B.3656.

Ugyanezek a számok b-alapú számrendszerben felírva \(\displaystyle F=0{,}2525\ldots=0{,}\dot2\dot5\) és \(\displaystyle G=0{,}5252\ldots=0{,}\dot5\dot2\). Határozzuk meg az a és a b számokat.

(4 pont)

Megoldás: Mivel m alapú számrendszerben a \(\displaystyle 0,0101\ldots=0,\dot0\dot1\) számot m²-1-gyel szorozva éppen 1-et kapunk, a feladat feltételei alapján

\(\displaystyle F={3a+7\over a^2-1}={2b+5\over b^2-1}\quad{\hbox{\rm\'es}}\quad G={7a+3\over a^2-1}={5b+2\over b^2-1},\)

ahonnan

\(\displaystyle F+G={10a+10\over a^2-1}={7b+7\over b^2-1}\quad{\hbox{\rm\'es}}\quad G-F={4a-4\over a^2-1}={3b-3\over b^2-1}.\)

Mivel a,b\(\displaystyle \ge\)2, az első összefüggésből a+1-gyel illetve b+1-gyel történő egyszerűsítés majd átrendezés után a 10(b-1)=7(a-1) egyenletre jutunk. Hasonlóképpen adódik a második összefüggésből a 4(b+1)=3(a+1) egyenlet. Az így kapott kétismeretlenes lineáris egyenletrendszer egyetlen megoldása a=11, b=8.

B.3657.

(4 pont)

Megoldás: Legyen a háromszög két befogója a\(\displaystyle \le\)b, átfogója c, félkerülete s. Ekkor a beírt kör érintési pontjai a befogókon a derékszögű csúcstól s-c távolságra helyezkednek el, vagyis a beírt kör sugara s-c. Hasonlóképpen a hozzáírt körök sugaraira s-a, s-b, illetve s adódik. Mivel s-c<s-b\(\displaystyle \le\)s-a<s, a négy szám csak akkor alkothatna 4 tagú számtani sorozatot, ha teljesülnének az

(s-b)-(s-c)=(s-a)-(s-b)=s-(s-a)

egyenlőségek. Ekkor azonban c-b=b-a=a, vagyis b=2a, c=3a lenne, ami ellentmond Pithagorasz tételének. Ilyen derékszögű háromszög tehát nem létezik.

B.3658.

(3 pont)

Megoldás:

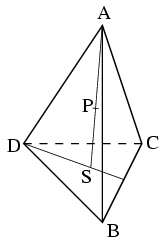
Az A csúcsból a BCD lapra állított merőleges szakasz talppontja egybeesik a BCD lap S súlypontjával, mely 1:2 arányban osztja az FD szakaszt, ahol F a BC él felezőpontja. Ha AB=1 és PS=x, akkor \(\displaystyle FD=\sqrt{3}/2\), \(\displaystyle FS=FD/3=1/\sqrt{12}\), a térbeli Pithagorasz tétel alapján pedig

\(\displaystyle PB^2=BF^2+FS^2+SP^2={1\over4}+{1\over12}+x^2={1\over3}+x^2.\)

Szimmetria okok miatt az egyenlő hosszú PB, PC, PD szakaszok akkor lesznek páronként egymásra merőlegesek, ha BC²=PB²+PC², vagyis PB²=1/2, ahonnan \(\displaystyle x=1/\sqrt{6}\) adódik. Mivel \(\displaystyle SD=(2/3)FD=1/\sqrt{3}\), a Pithagorasz tétel alapján felírt AD²=SD²+AS² miatt \(\displaystyle AS=\sqrt{2/3}=2/\sqrt{6}=2x\), tehát a P pont felezi az AS szakaszt.

B.3659.

(4 pont)

Megoldás: Ha létezik ilyen felbontás, akkor olyan felbontás is létezik, amelyben a két másodfokú tényező főegyütthatója egyaránt 1. Keressük tehát a felbontást

x⁴+tx²+1=(x²+bx+c)(x²+Bx+C)

alakban. A szorzatban x³ együtthatója b+B, a szorzat konstans tagja pedig cC, ahonnan B=-b, C=1/c adódik. Mivel x együtthatója bC+Bc=0, kapjuk hogy b/c-bc=b(1-c²)/c=0. Ezek szerint vagy b=0, vagy pedig c=\(\displaystyle \pm\)1.

Az első esetben az \(\displaystyle x^4+tx^2+1=(x^2+c)(x^2+{1\over c})\) összefüggésnek kell fennállnia, ami az eddigiek alapján pontosan akkor következik be, ha a másodfokú tag együtthatója mindkét oldalon ugyanaz, vagyis ha \(\displaystyle t=c+{1\over c}\). Ilyen c valós szám pontosan akkor található, ha |t|\(\displaystyle \ge\)2. Ha -2<t<2, akkor másfajta felbontás után kell tehát néznünk, ezért most c=\(\displaystyle \pm\)1. Most az

x⁴+tx²+1=(x²+bx+1)(x²-bx+1)

összefüggést vizsgálva, ez pontosan akkor áll fenn, ha t=2-b², ilyen b pedig t\(\displaystyle \le\)2 esetén mindig található. A feladatot tehát megoldottuk t minden lehetséges értékére. Jegyezzük meg, hogy a fenti megoldást kicsit jobban végiggondolva az összes elképzelhető felbontás is megtalálható. (Hogyan?)

B.3660.

Ha A, B és C egy háromszög csúcsai, akkor jelölje M_A és M_B a háromszög A, illetve B csúcsából induló magasságvonalnak a háromszög köré írt körrel vett metszéspontját, F_C pedig a C csúcsnál lévő szög szögfelezőjének a körülírt körrel vett metszéspontját.

Határozzuk meg az összes olyan hegyesszögű ABC háromszöget, amelyre az M_A, M_B és F_C pontok valamilyen sorrendben megegyeznek az X, Y és Z pontokkal.

(4 pont)

Megoldás: Ha ABC egy hegyesszögű háromszög, melynek szögeit a szokásos módon \(\displaystyle \alpha\), \(\displaystyle \beta\) és \(\displaystyle \gamma\) jelöli, akkor az ABC háromszög köré írt kör AB, BC, CA íveit az F_C, M_A, M_B pontok olyan F_CB, BM_A, M_AC, CM_B, M_BA, AF_C ívekre osztják, melyekhez tartozó kerületi szögek nagysága rendre \(\displaystyle \gamma\)/2, 90^o-\(\displaystyle \beta\), 90^o-\(\displaystyle \gamma\), 90^o-\(\displaystyle \gamma\), 90^o-\(\displaystyle \alpha\), illetve \(\displaystyle \gamma\)/2. Az F_CM_A, M_AM_B, M_BF_C ívekhez tartozó középponti szögek nagysága tehát rendre 180^o-2\(\displaystyle \beta\)+\(\displaystyle \gamma\), 360^o-4\(\displaystyle \gamma\), 180^o-2\(\displaystyle \alpha\)+\(\displaystyle \gamma\). Az F_C, M_A, M_B pontok köré írt kör megegyezik az ABC háromszög köré írható körrel, az említett három középponti szög ismeretetében pedig előbb \(\displaystyle \gamma\), majd \(\displaystyle \alpha\) és \(\displaystyle \beta\) is egyértelműen meghatározató, és kielégíti az \(\displaystyle \alpha\)+\(\displaystyle \beta\)+\(\displaystyle \gamma\)=180^o összefüggést. Ha az így kiszámolt \(\displaystyle \alpha\), \(\displaystyle \beta\), \(\displaystyle \gamma\) szögek valamelyike nem hegyesszög, akkor lehetetlen helyzetből indultunk ki, ha viszont mindhárom szög hegyesszög, akkor a fent leírtak alapján az A,B,C pontokat az F_C, M_A, M_B pontok köré írt körön egyértelműen kijelölhetjük: A az F_CM_B ívnek az a pontja, melyre az AF_C ívhez tartozó középponti szög éppen a kiszámolt \(\displaystyle \gamma\) szöggel egyenlő, és így tovább.

Minden egyes keresett háromszögre tehát a 180^o-2\(\displaystyle \beta\)+\(\displaystyle \gamma\), 360^o-4\(\displaystyle \gamma\), 180^o-2\(\displaystyle \alpha\)+\(\displaystyle \gamma\) szögek valamilyen sorrendben meg kell egyezzenek a megadott 60^o, 100^o és 200^o szögekkel. 6 különböző lehetőség képzelhető el. Az első 2 lehetőségben az M_AM_B ívhez tartozik a 200^o-os középponti szög, ekkor tehát F_C a másik két ív közös végpontja, \(\displaystyle \gamma\)=40^o, ami az A,B pontok helyét már egyértelműen kijelöli az F_CM_B, illetve F_CM_A íveken. Ha az utóbbihoz tartozó középponti szög 100^o-os, akkor \(\displaystyle \alpha\)=80^o és \(\displaystyle \beta\)=60^o, ellenkező esetben pedig \(\displaystyle \alpha\)=60^o és \(\displaystyle \beta\)=80^o. Ez azt jelenti, hogy mindkét esetben ugyanazt a háromszöget kapjuk, csakhogy a csúcsok megnevezésénél az A és B betűk szerepe felcserélődik. Ha az M_AM_B ívhez a 100^o-os középponti szög tartozna, akkor \(\displaystyle \gamma\)=65^o, az \(\displaystyle \alpha\) és \(\displaystyle \beta\) szögek közül pedig az egyikre 22,5^o, a másikra 92,5^o adódna, ez tehát nem lehetséges. Végül, ha az M_AM_B ívhez a 60^o-os középponti szög tartozik, akkor \(\displaystyle \gamma\)=75^o, az \(\displaystyle \alpha\) és \(\displaystyle \beta\) szögek közül pedig az egyikre 27,5^o, a másikra 77,5^o adódik. Az első két esethez hasonló módon tehát most is egyértelműen meghatározhatjuk a két megoldást, amely végeredményben ugyanazt a háromszöget adja.

Összefoglalva, a megadott X,Y,Z pontok pontosan 4 különböző ABC hegyesszögű háromszöget határoznak meg, ha azonban a háromszög csúcsainak megnevezésétől eltekintünk, csak két valóban különböző háromszöget találunk.

B.3661.

(5 pont)

Megoldás: Teljes indukcióval könnyen igazolható, hogy mindhárom sorozat elemei pozitív számok. Ezért az a_n=x_ny_n+y_nz_n+z_nx_n jelöléssel a₁=11, és minden pozitív egész n-re

\(\displaystyle a_{n+1}=a_n+3+\Bigl({y_n\over x_n}+{z_n\over y_n}+{x_n\over z_n}\Bigr)+ \Bigl({1\over x_ny_n}+{1\over y_nz_n}+{1\over z_nx_n}\Bigr\)a_n+6,">

ugyanis a számtani és mértani közepek között fennálló egyenlőtlenség alapján

\(\displaystyle {1\over3}\Bigl({y_n\over x_n}+{z_n\over y_n}+{x_n\over z_n}\Bigr)\ge\root3\of{{y_n\over x_n}\cdot{z_n\over y_n}\cdot{x_n\over z_n}}=1.\)

Innen ismét n szerinti teljes indukcióval kapjuk, hogy a_n+1>a₁+6n, vagyis a₂₀₀>11+6^.199>1200, amiértis az x₂₀₀y₂₀₀, y₂₀₀z₂₀₀, z₂₀₀x₂₀₀ számok valamelyike szükségképpen nagyobb mint 400. Ezen szám két (pozitív) szorzótényezője közül legalább az egyik nagyobb, mint 20, ami igazolja a feladat állítását.