A számítástechnika-versenyben kitűzött feladatok 2003. május

Kérjük, olvassa el a versenykiírást.

I. 55. Erősen összetett számoknak nevezzük azokat az (1-nél nagyobb) természetes számokat, amelyek osztóinak a száma nagyobb, mint bármely nála kisebb természetes szám osztóinak a száma.

Készítsünk programot (i55.pas, ...), amely adott N-re (1\(\displaystyle \le\)N \(\displaystyle \le\)1 000 000) kiírja N-ig az erősen összetett számokat.

(10 pont)

I. 56. Készítsünk programot (i56.pas, ...), amely megrajzolja a hold egy adott fázisát. A telihold egy festett kör, az újhold pedig egy üres kör legyen, melynek középpontja a képernyő közepe, sugara pedig 100 képpontnyi. A program paramétere legyen a holdsarló átmérője, amit az alábbi ábra szerint értelmezünk!

Példa:

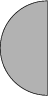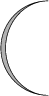200	140	100	10

(10 pont)

I. 57. Egy n-edfokú P(x) polinomot az együtthatóival adunk meg:

P(x) = a₀ + a₁ x + a₂ x² + ...+ a_n xⁿ.

A polinom deriváltja eggyel kisebb fokszámú polinom:

P'(x) = a₁ + 2a₂ x + 3a₃ x² + ...+ na_n x^n-1.

Az így kapott polinomot tovább deriválhatjuk, amíg az összes együttható nullává nem válik.

Készítsünk táblázatot (i57.xls), amely egy legfeljebb 10-edfokú polinom deriváltjait adja meg az alábbi formában:

(10 pont)

A számítástechnika feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2003. június 13.