 | A számítástechnika-versenyben
kitűzött feladatok |
Kérjük, olvassa el a versenykiírást.
I. 58. N-jegyű társas számoknak hívjuk a legfeljebb N-jegyű természetes számok egy a1, a2, ..., an sorozatát, amelyre igaz, hogy a1 valódi osztóinak az összege a2, a2 valódi osztóinak az összege a3, ..., an valódi osztóinak az összege pedig a1. (Megjegyzés: a társas számok a barátságos számok általánosítása.)
Készítsünk programot (i58.pas, ...), amely beolvassa N értékét (1 \(\displaystyle \le\)N \(\displaystyle \le\)8), majd kiírja az i58.ki szöveges állományba az összes N-jegyű társas szám közül azokat, amelyek legkisebbike az [X;Y] intervallumba esik.
Beküldendő az N=7, X=2, Y=9 999 999 paraméterekre készült eredmény állomány.
Példa ötjegyű társas számokra a [10000;13000] intervallumból:
10744 10856 12285 14595 12496 14288 15472 14536 14264. |
Példa háromjegyű társas számokra a [200;230] intervallumból:
220 284. |
(10 pont)
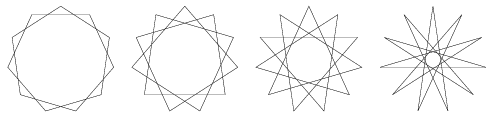
I. 59. Egy szabályos N oldalú sokszög egy csúcsát összekötjük az őt követő K-adik csúccsal, azt az őt követő K-adikkal, és így tovább, amíg vissza nem érünk a kezdő csúcshoz. Ha K\(\displaystyle \ge\)2 és útközben az N-szög valamennyi csúcsát bejártuk, akkor ún. szabályos N-ágú csillagot kapunk.
Készítsünk programot (i59.pas, ...), amely beolvassa N értékét (5 \(\displaystyle \le\)N \(\displaystyle \le\)100), majd kirajzolja az összes, egymástól különböző szabályos N-ágú csillagot. Csak azok az esetek érdekesek, amikor csillag keletkezik.
Példa: N=11-re az alábbi 4, különböző szabályos csillagot kapjuk:
(10 pont)
I. 60. Az erősen összetett számokhoz (lásd az I. 55.-ös feladatot a 2003. szeptemberi számban) hasonlók azok az ún. erősebben összetett [A;B]-intervallumbeli természetes számok, amelyek osztóinak a száma nagyobb vagy egyenlő, mint bármely [A;B] intervallumbeli kisebb természetes szám osztóinak a száma.
Készítsünk táblázatot (i60.xls), amely adott A, B-re (1\(\displaystyle \le\)A \(\displaystyle \le\)B \(\displaystyle \le\)1000) kiírja az összes [A;B]-intervallumbeli egész számokat, piros színnel kiemelve az erősebben összetett számokat.
| A=10 | B=25 |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 | |
| 22 | |
| 23 | |
| 24 | |
| 25 |
(10 pont)
A számítástechnika feladatok megoldásai a következő címre küldendők:
Cím: szamtech@komal.hu

