A 2003. decemberi C-jelű matematika gyakorlatok megoldása

A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.

C. 740 Határozzuk meg azokat a pozitív egész számokat, amelyek másfélszer akkorák, mint a számjegyeik szorzata.

Megoldás. Ha a szám (k+1)-jegyű és első jegye a, akkor a szám értéke legalább 10^ka, számjegyei szorzatának másfélszerese pedig legfeljebb 1,5^.9^ka. Mivel 10^k>1,5^.9^k ha k $\displaystyle \ge$ 4, ezért a keresett számok legfeljebb négyjegyűek.

Egyjegyű szám nyilván nem jó. Ha a kétjegyű $\displaystyle \overline{ab}$ jó, akkor

10a+b=1,5ab,

azaz

2b=(3b-20)a.

Tehát 3b $\displaystyle \ge$ 20, azaz b csak 7,8 vagy 9 lehet. Ezeket behelyettesítve csak b=8 esetén lesz a egyjegyű egész, ekkor a=4. Könnyen ellenőrizhető, hogy a 48 eleget tesz a feltételeknek.

Ha a háromjegyű $\displaystyle \overline{abc}$ jó, akkor

100a+10b+c=1,5abc,

azaz

20b+2c=(3bc-200)a.

Tehát 3bc $\displaystyle \ge$ 200, azaz (b,c) csak a (9,8), (8,9) és a (9,9) rendezett párok valamelyike lehet. Ezeket behelyettesítve viszont a nem lesz egész, tehát nincs háromjegyű megoldás.

Ha a négyjegyű $\displaystyle \overline{abcd}$ jó, akkor

1000a+100b+10c+d=1,5abcd,

azaz

200b+20c+2d=(3bcd-2000)a.

Tehát 3bcd $\displaystyle \ge$ 2000, azaz (b,c,d) csak (9,9,9) lehet. Ezt behelyettesítve viszont a nem lesz egész, tehát négyjegyű megoldás sincs.

Vagyis a feladat feltételeinek egyetlen szám, a 48 tesz eleget.

C. 741. Szerkesszünk háromszöget, ha adott két oldala, a és b, továbbá tudjuk, hogy (a szokásos jelölésekkel) $\displaystyle \alpha$ =2 $\displaystyle \beta$ .

Megoldás. Tekintsük a feladatot megoldottnak. Legyenek a háromszög csúcsai a szokásos jelölésekkel A,B,C; D pedig legyen az AB egyenesnek az a B-től különböző pontja, melyre CD=CB. Ekkor a CDB háromszög egyenlő szárú, vagyis CDB $\displaystyle \angle$ =CBD $\displaystyle \angle$ = $\displaystyle \beta$ . A CDA háromszög A-nál lévő külső szöge CAB $\displaystyle \angle$ =2 $\displaystyle \beta$ , ezért DCA $\displaystyle \angle$ = CAB $\displaystyle \angle$ - CDA $\displaystyle \angle$ = $\displaystyle \beta$ , vagyis a CDA háromszög is egyenlő szárú, DA=AC=b.

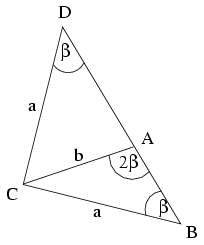
Ezek alapján a szerkesztés: a és b ismeretében megszerkesztjük a DAC háromszöget, majd a DA oldal A-n túli meghosszabbítását a C középpontú a sugarú körrel elmetszve megkapjuk a B csúcsot. Az így szerkesztett ABC háromszög nyilván eleget tesz a feltételeknek. A megoldások száma egy, ha 2b>a, ha pedig ez az egyenlőtlenség nem teljesül, akkor nincs megoldás.

C. 742.

Szeretnénk egy kerítés elkorhadt léceit 2,5 méter hosszú szakaszon 3 cm vastag új lécekre kicserélni. Az egyik fa törzse éppen megfelelő magasságú, és belőle egy 30 cm átmérőjű kör alapú egyenes henger használható fel. A kapott léceket szorosan egymás mellett szeretnénk felállítani úgy, hogy a szélesebb oldaluk nézzen befelé.

Elkészíthető-e a kerítés, ha veszteség nélkül tudjuk méretre szabni a fatörzset?

Megoldás.

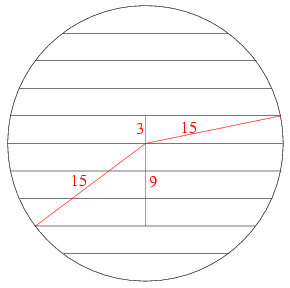
A lécek 3 cm széles körszeletek lesznek. Összhosszuk Pitagorasz tételét használva:

$\displaystyle 2\big(30+2(\sqrt{225-9}+\sqrt{225-36}+\sqrt{225-81}+\sqrt{225-144})\big)=257,72 \,\,{\rm cm}$

tehát elkészíthető belőlük a kerítés.

C. 743.

Oldjuk meg az

$\displaystyle \log_x\left(2{,}5-\frac{1}{x}\right$ 1 "> egyenlőtlenséget.

Megoldás. Mivel a logaritmus alapja 1-től különböző pozitív szám, ezért 0<x $\displaystyle \ne$ 1. Továbbá teljesülnie kell a 2,5-1/x>0 egyenlőtlenségnek is, tehát x>0,4.

Tudjuk, hogy log_xx=1. Az x $\displaystyle \mapsto$ log_ax függvény a>1 esetén szigorúan monoton növekvő, míg a<1 esetén szigorúan monoton csökkenő. Ennek megfelelően ha x>1, akkor eredeti egyenlőtlenségünkből

$\displaystyle 2,5-\frac{1}{x$ x,\qquad\qquad(1)">

míg x<1 esetén

\(\displaystyle 2,5-\frac{1}{x}

következik. A 2,5-1/x=x egyenletet átalakítva az

x²-2,5x+1=0

egyenletet kapjuk, aminek gyökei x₁=1/2 és x₂=2. Pozitív x-ekre az (1) egyenlőtlenség tehát akkor teljesül, ha 1/2<x<2, míg a (2) akkor, ha x<1/2 vagy ha 2<x.

Eredeti egyenlőtlenségünk megoldása tehát:

0,4<x<0,5 vagy 1<x<2.

C. 744. Hányféleképpen helyezhető el a 8x8-as sakktáblán egy 5 egységnyi oldalú négyzet úgy, hogy minden csúcsa egy-egy mező középpontjába essék? (A tükrözéssel és forgatással egymásba vihető megoldásokat nem tekintjük különbözőknek.)

Megoldás. Ha az 5 egység oldalú négyzet oldalai párhuzamosak a sakktábla oldalaival, akkor tükrözésekkel és forgatásokkal elérhető, hogy a négyzet egyik csúcsa a sakktábla bal felső sarkában lévő 2x2-es résztábla valamelyik mezőjének középpontjában legyen, mert a sakktábla mezőinek középpontjai egy 7 egység oldalú négyzetet alkotnak. Ezen mezők közül bármelyik lehet a kis négyzet bal felső sarka, tehát ilyen típusú kis négyzetből 4 darab van.

Ha a kis négyzet oldalai nem párhuzamosak a sakktábla oldalaival, akkor a kis négyzet két szomszédos csúcsa, valamint a sakktábla egyik mezőjének középpontja olyan derékszögű háromszöget alkot (lásd az ábrát), amelynek átfogója 5 egység, befogóinak hossza pedig egész számú egység. Ez csak úgy lehet, ha a két befogó hossza 3 illetve 4 egység. Ilyen helyzetű kis négyzet csak egyféleképp helyezhető el.

Tehát összesen ötféleképp helyezhető el a kis négyzet a feltételeknek megfelelő módon.

Már regisztráltál?
Új vendég vagy?