A számítástechnika-versenyben kitűzött feladatok 2004. január

Kérjük, olvassa el a versenykiírást.

I. 67. Egy körmérkőzéses bajnokságban N csapat szerepel (2\(\displaystyle \le\)N\(\displaystyle \le\)100, N páros). Készítsünk programot (i67.pas, ...), amely előállítja az egyes fordulók sorsolását úgy, hogy mindenki játsszon minden fordulóban, s mindenki mindenkivel pontosan egyszer találkozzon.

Példa: N=4 esetén:

(10 pont)

I. 68. Egy bináris fát mindig megadhatunk egy zárójeles kifejezéssel. (X) mindig egy egyelemű fát jelöl, ((X)X(X)) pedig egy olyan fát, amelyben a gyökérelemtől balra és jobbra is pontosan egy egyelemű fa található.

Példák:

((X)X)
(X(X))
(((X(X))X)X((X)X((X)X(X))))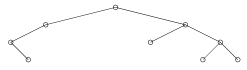

Készítsünk programot (i68.pas, ...), amely beolvas egy bináris fát leíró zárójeles kifejezést (legalább 1 elem biztosan van benne), majd kirajzolja a bináris fát.

(10 pont)

I. 69. Készítsünk táblázatot (i69.xls), amelynek első és második sorába egy-egy szigorúan monoton növekedő, egész számokból álló, legfeljebb 100 elemű számsorozatot írhatunk. Mindkét számsorozatot egy-egy üres cella zárja le. A táblázat harmadik sorában jelenjen meg a két számsorozat ,,összefésülésével'' nyert sorozat, azaz az a szigorúan monoton növekedő számsorozat, amely a két sorozat számait tartalmazza, de ha egy szám mindkettőben előfordul, azt csak egyszer írjuk föl. (Makrók használata esetén a pontszám fele kapható.)

(10 pont)

A számítástechnika feladatok megoldásai a következő címre küldendők:

A beküldési határidő: 2004. február 13.