Solutions for advanced problems "A" in February, 2004

In this page only the sketch of the solutions are published; in some cases only the final results. To achieve the maximum score in the competition more detailed solutions needed.

A. 338. For any positive integer n denote the closest integer to $\displaystyle \sqrt{n}$ by f(n). Calculate the value of the sum

$\displaystyle \sum_{n=1}^\infty\frac{2^{f(n)}+2^{-f(n)}}{2^n}.$

Solution. It is easy to check that for each positive integer k, f(n)=k if and only if k²-k+1 $\displaystyle \le$n $\displaystyle \le$k²+k. Grouping the terms by the values of f(n),

$\displaystyle \sum_{n=1}^{m^2+m}\frac{2^{f(n)}+2^{-f(n)}}{2^n} = \sum_{k=1}^m\sum_{n=k^2-k+1}^{k^2+k}\frac{2^k+2^{-k}}{2^n} =$

$\displaystyle = \sum_{k=1}^m(2^k+2^{-k})\left(\frac1{2^{k^2-k}}-\frac1{2^{k^2+k}}\right) = \sum_{k=1}^m\left(\frac1{2^{(k-2)k}}-\frac1{2^{k(k+2)}}\right) =$

$\displaystyle = \frac1{2^{(-1)\cdot1}}+\frac1{2^{0\cdot2}} -\frac1{2^{(m-2)m}}-\frac1{2^{m(m+2)}} = 3-\frac1{2^{(m-2)m}}-\frac1{2^{m(m+2)}}.$

The last two quantites converge to 0, so

$\displaystyle \sum_{n=1}^\infty\frac{2^{f(n)}+2^{-f(n)}}{2^n} = \lim_{m\to\infty}\sum_{n=1}^{m^2+m}\frac{2^{f(n)}+2^{-f(n)}}{2^n} =3.$

A. 339. We want to select 4 tuples from a 28-element set with the following properties: a) Any two 4-tuple has at most two common elements; b) for any element x and 4-tuple A that is not containing x there exists at least one 4-tuple B that contains x-et and it has exactly two common elements with A. Is it possible to select such a system of 4-tuples?

Solution. There exists such a system of sets. Consider the 28 edges of a a complete graph on 8 vertices. Select those 4-tuples of edges which span all vertices. The set of such 4-tuplets has the required properties.

A. 340. Is it possible that the length of the intersection of a circular disc of unit radius and a parabola is greater than 4 units?

Soultion. Yes. Let the center of the circle be the origin of the Cartesian co-ordinate system, let the axis of the parabola be the y-axis and let its vertex be at (0,-1) (see Figure) and suppose that it contains points ($\displaystyle \pm$sin $\displaystyle \alpha$,cos $\displaystyle \alpha$) where $\displaystyle \alpha$ is a small positive angle.

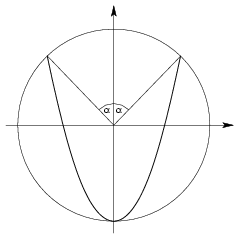
The equation of the parqabola is

$\displaystyle y={1+\cos\alpha\over\sin^2\alpha}x^2+1= {1\over2\sin^2{\alpha\over2}}x^2+1.$

The length of the arc is

$\displaystyle l=\int\limits_{-\sin\alpha}^{\sin\alpha}\sqrt{1+{x^2\over\sin^4{\alpha\over2}}}dx.$

Substituting $\displaystyle u-{1\over u}={2x\over\sin^2{\alpha\over2}}$ and denoting $\displaystyle {\sin\alpha\over\sin^2{\alpha\over2}}=2\ctg{\alpha\over2}$ by A,

$\displaystyle \sqrt{1+{x^2\over\sin^4{\alpha\over2}}}={u+{1\over u}\over2}$

and

$\displaystyle l= \int\limits_{\sqrt{1+A^2}-A}^{\sqrt{1+A^2}+A} {u+{1\over u}\over2}\cdot\bigg({\sin^2{\alpha\over2}\over2}\Big(u-{1\over u}\Big)\bigg)'du = {\sin^2{\alpha\over2}\over4} \int\limits_{\sqrt{1+A^2}-A}^{\sqrt{1+A^2}+A} \bigg(u+{2\over u}+{1\over u^3}\bigg)du =$

$\displaystyle = {\sin^2{\alpha\over2}\over4}\bigg(4A\sqrt{1+A^2}+ 4\log\big(A+\sqrt{1+A^2}\big)\bigg).$

By the inequalities $\displaystyle \sqrt{1+A^2$A=2\ctg{\alpha\over2}>{4\over\alpha}">, $\displaystyle \sin\alph$\alpha-{1\over6}\alpha^3"> and $\displaystyle \sin{\alpha\over2${\alpha\over4}">,

$\displaystyle {\sin^2{\alpha\over2}\over4}\cdot4A\sqrt{1+A^2} = \sin\alpha\sqrt{1+A^2$\bigg(\alpha-{1\over6}\alpha^3\bigg){4\over\alpha} = 4-{2\over3}\alpha^2, ">

$\displaystyle \sin^2{\alpha\over2}\log\big(A+\sqrt{1+A^2}\big$ {\alpha^2\over16}\log{8\over\alpha} ">

and

$\displaystyle$4+\alpha^2\bigg({1\over16}\log{8\over\alpha}-{2\over3}\bigg).">

If $\displaystyle \alpha$ sufficiently small, then $\displaystyle {1\over16}\log{8\over\alpha${2\over3}"> and l>4.