 |
A 2004 februári A-jelű matematika feladatok megoldása |
A közöltek csak megoldásvázlatok, esetleg csak végeredmények. A maximális pontszám eléréséhez általában ennél részletesebb megoldás szükséges. A részletes megoldásokat a beküldött dolgozatok alapján a KöMaL-ban folyamatosan közöljük.
A. 338. Tetszőleges pozitív egész n számra jelölje f(n) a \(\displaystyle \sqrt{n}\)-hez legközelebb eső egészt. Számítsuk ki a
\(\displaystyle \sum_{n=1}^\infty\frac{2^{f(n)}+2^{-f(n)}}{2^n} \)
összeg értékét.
Megoldás. Mivel a sor tagjai pozitívak, a részletösszegek tetszőleges részsorozatának ugyanaz a határértéke, ezért elég egy alkalmas részsorozatot vizsgálni.
Könyen ellenőrizhető, hogy tetszőleges k pozitív egészre f(n)=k akkor teljesül, ha k2-k+1 \(\displaystyle \le\)n \(\displaystyle \le\)k2+k. Az összeget f(n) értéke szerint csoportosítva,
\(\displaystyle \sum_{n=1}^{m^2+m}\frac{2^{f(n)}+2^{-f(n)}}{2^n} = \sum_{k=1}^m\sum_{n=k^2-k+1}^{k^2+k}\frac{2^k+2^{-k}}{2^n} =\)
\(\displaystyle = \sum_{k=1}^m(2^k+2^{-k})\left(\frac1{2^{k^2-k}}-\frac1{2^{k^2+k}}\right) = \sum_{k=1}^m\left(\frac1{2^{(k-2)k}}-\frac1{2^{k(k+2)}}\right) =\)
\(\displaystyle = \frac1{2^{(-1)\cdot1}}+\frac1{2^{0\cdot2}} -\frac1{2^{(m-2)m}}-\frac1{2^{m(m+2)}} = 3-\frac1{2^{(m-2)m}}-\frac1{2^{m(m+2)}}. \)
Az utolsó két tag 0-hoz tart, ezért
\(\displaystyle \sum_{n=1}^\infty\frac{2^{f(n)}+2^{-f(n)}}{2^n} = \lim_{m\to\infty}\sum_{n=1}^{m^2+m}\frac{2^{f(n)}+2^{-f(n)}}{2^n} =3. \)
Megjegyzés. Több versenyző nem indokolta meg, hogy miért elég a részletösszegeknek egy alkalmas részsorozatát vizsgálni, és annak vizsgálatáról is elfeledkezett, hogy az utolsó tagok 0-hoz tartanak-e. Ők 4 pontot kaptak.
A. 339. Egy 28-elemű halmazból 4-elemű részhalmazokat akarunk kiválasztani a következő tulajdonságokkal:
a) Bármelyik két kiválasztott négyesnek legfeljebb két közös eleme legyen;
b) Ha x egy tetszőleges elem és A egy olyan négyes, amely nem tartalmazza x-et, akkor létezzen legalább egy olyan B négyes is, amely az x-et tartalmazza, és A-val pontosan két közös eleme van.
Lehetséges-e ilyen négyeseket kiválasztani?
Megoldás. Ilyen halmazrendszer létezik. Tekintsük egy 8-pontú teljes gráf éleit; ezek száma éppen 28. Válasszuk ki azokat az élnégyeseket, amelyek mind a 8 csúcsot pontosan egyszer tartalmazzák. Egy-egy ilyen négyest bármelyik három éle meghatározza, ezért ha két négyesnek van három közös eleme, akkor a két négyes ugyanaz. Az a) tulajdonság tehát teljesül.
Ha A=(a1,a2) egy tetszőleges él, x pedig egy olyan négyes, amely nem tartalmazza A-t, akkor x={(a1,b1),(a2,b2),(c1,c2),(d1,d2)} alakú. Ebben az esetben a b) feltételnek eleget tesz az y={(a1,a2),(b1,b2),(c1,c2),(d1,d2)} négyes.
A. 340. Lehet-e egy egységnyi sugarú kör belsejében fekvő parabolaív hossza 4 egységnél nagyobb?
Megoldásvázlat. A válasz igen. Helyezzük a kör középpontját a derékszögű koorrdinátarendszer origójába, és tekintsük azt a parabolát, amelynek tengelye az y-tengely, csúcsa a (0,-1) pont és átmegy az (\(\displaystyle \pm\)sin \(\displaystyle \alpha\),cos \(\displaystyle \alpha\)) pontokon, ahol \(\displaystyle \alpha\) egy kicsi szög.
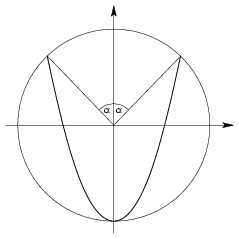
Mint könnyen ellenőrizhető, a parabola egyenlete
\(\displaystyle y={1+\cos\alpha\over\sin^2\alpha}x^2+1= {1\over2\sin^2{\alpha\over2}}x^2+1.\)
A parabolaív hosszát az
\(\displaystyle l=\int\limits_{-\sin\alpha}^{\sin\alpha}\sqrt{1+{x^2\over\sin^4{\alpha\over2}}}dx\)
integrál adja meg. Az \(\displaystyle u-{1\over u}={2x\over\sin^2{\alpha\over2}}\) helyettesítést és az \(\displaystyle A={\sin\alpha\over\sin^2{\alpha\over2}}=2\ctg{\alpha\over2}\) jelölést alkalmazva,
\(\displaystyle \sqrt{1+{x^2\over\sin^4{\alpha\over2}}}={u+{1\over u}\over2}\)
és
\(\displaystyle l= \int\limits_{\sqrt{1+A^2}-A}^{\sqrt{1+A^2}+A} {u+{1\over u}\over2}\cdot\bigg({\sin^2{\alpha\over2}\over2}\Big(u-{1\over u}\Big)\bigg)'du = {\sin^2{\alpha\over2}\over4} \int\limits_{\sqrt{1+A^2}-A}^{\sqrt{1+A^2}+A} \bigg(u+{2\over u}+{1\over u^3}\bigg)du =\)
\(\displaystyle = {\sin^2{\alpha\over2}\over4}\bigg(4A\sqrt{1+A^2}+ 4\log\big(A+\sqrt{1+A^2}\big)\bigg).\)
Az \(\displaystyle \sqrt{1+A^2\)A=2\ctg{\alpha\over2}>{4\over\alpha}">, a \(\displaystyle \sin\alph\)\alpha-{1\over6}\alpha^3"> és \(\displaystyle \sin{\alpha\over2\){\alpha\over4}"> becsléseket beírva
\(\displaystyle {\sin^2{\alpha\over2}\over4}\cdot4A\sqrt{1+A^2} = \sin\alpha\sqrt{1+A^2\)\bigg(\alpha-{1\over6}\alpha^3\bigg){4\over\alpha} = 4-{2\over3}\alpha^2, ">
\(\displaystyle \sin^2{\alpha\over2}\log\big(A+\sqrt{1+A^2}\big\) {\alpha^2\over16}\log{8\over\alpha} ">
és
\(\displaystyle \)4+\alpha^2\bigg({1\over16}\log{8\over\alpha}-{2\over3}\bigg).">
Ha \(\displaystyle \alpha\) kellően kicsi, akkor \(\displaystyle {1\over16}\log{8\over\alpha\){2\over3}"> és l>4.
Fórum:

